Тема: Неопределенный интеграл.
Первообразная функции.
Для всякой математической операции прямого действия всегда существует операция обратного действия. Сложение и вычитание, умножение и деление, логарифмирование и потенцирование, дифференцирование и интегрирование.
Прямая задача: дана функция f(x), найти производную f’(x)
Обратная задача: дана производная f’(x), восстановить функцию f(x)
Опр. Первообразной от функции f(x) наз. другая функция F(x), производная от которой равна f(x)
F’(x) = f(x) (1) или dF(x) = f(x) dx (2)
Знак d (оператор) означает, что над функцией F(x) производится операция вычисления дифференциала. Знак обратной операции, для перехода от F’(x) к F(x), имеет вид  , а сама операция отыскания первообразной функции наз. интегрированием.
, а сама операция отыскания первообразной функции наз. интегрированием.
Пр. F(x) = 2x2 является первообразной функции f(x) = 4x. Действительно,
F’(x) = (2x2)’ = 4x = f(x). Функции 2x2 + 6, 2x2 + 8, 2x2 + const также являются первообразными для 4х. Общее свойство: Первообразная любой функции определяется с точностью до константы.
Опр. Неопределенным интегралом от функции f(x) наз.совокупность всех её первообразных  dF(x) =
dF(x) =  f(x) dx = F(x) + C (3)
f(x) dx = F(x) + C (3)
Знаки прямойи обратной операций d и  взаимно уничтожают друг друга. Здесь f(x) – подынтегральная функция, f(x) dx -подынтегральное выражение, x - переменная интегрирования,
взаимно уничтожают друг друга. Здесь f(x) – подынтегральная функция, f(x) dx -подынтегральное выражение, x - переменная интегрирования,  - символ неопределённого интеграла, C - постоянная интегрирования.
- символ неопределённого интеграла, C - постоянная интегрирования.
График первообразной функции y = F(x) наз. и нтегральной кривой. Геометрически неопределенный интеграл представляет собой семейство интегральных кривых, полученных при их параллельном переносе вдоль оси Оу.
Проинтегрировать функцию значит определить вид другой функции, производная от которой дает исходную функцию.
Табличные интегралы.
Таблицу формул дифференцирования можно представить в следующем виде, если переписать её слева направо.
1.  xn dx =
xn dx =  + C (n ¹ -1); 2.
+ C (n ¹ -1); 2.  = ln |x| + C; 3.
= ln |x| + C; 3.  ex dx = ex + C;
ex dx = ex + C;
4.  ax dx =
ax dx =  + C; 5.
+ C; 5.  cos x dx = sin x + C; 6.
cos x dx = sin x + C; 6.  sin x dx = - cos x + C;
sin x dx = - cos x + C;
7. 
 = tg x + C; 8.
= tg x + C; 8. 
 = - ctg x + C; 9.
= - ctg x + C; 9.  tg x dx = - ln|cos x|+ C;
tg x dx = - ln|cos x|+ C;
10.  ctg x dx = ln|sin x| + C; 11.
ctg x dx = ln|sin x| + C; 11. 
 = arcsin x/a + C = - arccos x/a + C;
= arcsin x/a + C = - arccos x/a + C;
12. 
 = ln|x+
= ln|x+  | + C; 13.
| + C; 13. 
 = (1/a) arctg x/a + C;
= (1/a) arctg x/a + C;
Основные свойства неопределенного интеграла.
10. (  f(x) dx)’ = f(x), т.к. (F(x) + C)’ = F’(x) = f(x)
f(x) dx)’ = f(x), т.к. (F(x) + C)’ = F’(x) = f(x)
Производная от интеграла равна подынтегральной функции.
20. d (  f(x) dx) = (
f(x) dx) = (  f(x) dx)’dx = f(x) dx
f(x) dx)’dx = f(x) dx
Дифференциал от интеграла равен подынтегральному выражению
30.  d F(x) =
d F(x) =  F’(x) dx =
F’(x) dx =  f(x) dx = F(x) + C
f(x) dx = F(x) + C
Интеграл от дифференциала функции дает функцию плюс константа.
40.  a f(x) dx = a
a f(x) dx = a  f(x) dx, т.к. d (a F(x)) = a dF(x)
f(x) dx, т.к. d (a F(x)) = a dF(x)
Постоянный множитель выносится за знак интеграла.
50.  [f(x) + g(x)] dx =
[f(x) + g(x)] dx =  f(x) dx +
f(x) dx +  g(x) dx, т.к. производные совпадают.
g(x) dx, т.к. производные совпадают.
Интеграл от суммы функций равен сумме интегралов.
60. Инвариантность формы неопределенного интеграла: Переменную интегрирования х можно заменить в интеграле на произвольную дифференцируемую функцию u=u(x), т.е.
если  f(x) dx = F(x) + C (а), то
f(x) dx = F(x) + C (а), то  f(u(x)) du(x) = F(u(x)) + C (б).
f(u(x)) du(x) = F(u(x)) + C (б).
Док-во. Заменим х на u(x) в первообразной F(x). Получаем сложную функцию F(u(x)). Её дифференциал обладает свойством инвариантности формы:
d [F(u(x))] = F`x dx = F`udu, т.е. приращение функции dF получаем в результате изменения либо dx, либо du. Проинтегрируем это равенство  dF(u) =
dF(u) =  F`udu и оно превращается в интеграл (б):
F`udu и оно превращается в интеграл (б):  f(u) du = F(u) + C. Следствие. интегрирование сложной функции по переменной х можно заменить на интегрирование по сложному аргументу u(x). В этом случае в интегрировании участвует только внешняя функция и процедура интегрирования упрощается.
f(u) du = F(u) + C. Следствие. интегрирование сложной функции по переменной х можно заменить на интегрирование по сложному аргументу u(x). В этом случае в интегрировании участвует только внешняя функция и процедура интегрирования упрощается.
Пр.  esin x cos x dx =
esin x cos x dx =  esin x d(sin x) =
esin x d(sin x) =  eu du = eu + C = esin x + C, (u = sin x)
eu du = eu + C = esin x + C, (u = sin x)
Непосредственное интегрирование.
В наиболее простых случаях после некоторых преобразований функции интеграл удается свести к набору табличных интегралов или представить подынтегральное выражение как дифференциал некоторой функции, например, dx = 1/a d(ax + b),
x2 dx = 1/3 d(x3), cos 2x dx = d(sin 2x /2), 1/x dx = d(ln x). Такой прием интегрирования наз. н епосредственным.
 (3x2 – cos x + 6 /x)dx = 3
(3x2 – cos x + 6 /x)dx = 3  x2 dx -
x2 dx -  cos x dx + 6
cos x dx + 6  dx/x = x3 – sin x + 6 ln x + C
dx/x = x3 – sin x + 6 ln x + C

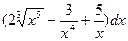 =
= 
 = 2(3/8)x8/3 - 3 x-3/(-3) + 5 ln x + C
= 2(3/8)x8/3 - 3 x-3/(-3) + 5 ln x + C
 cos 2x dx =
cos 2x dx =  d (sin 2x / 2) = (sin 2x / 2) + C
d (sin 2x / 2) = (sin 2x / 2) + C
Пр.  tg2x dx,
tg2x dx, 
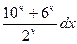 ,
, 
 ,
,  2x(1 + 3 x2 2-x) dx
2x(1 + 3 x2 2-x) dx
Метод замены переменных.
Всякую подынтегральную функцию f(x) можно представить как сложную, если ввести новую переменную интегрирования t, а такжепрямую и обратную зависимости x = g(t), t = g-1(x)  h(x), тогда
h(x), тогда
 f(x) dx =
f(x) dx =  f[g(t)] g’(t) dt = F(t) + C = F(h(x)) + C
f[g(t)] g’(t) dt = F(t) + C = F(h(x)) + C
Вспомогательный интеграл по новой переменной t может оказаться более простым для вычисления. После его вычисления делаем обратную замену t = h(x) и получаем решение исходного интеграла.
Пр.  esin x cos x dx = { пусть t = sin x, тогда dt = (sin x)’dx = cos x dx} =
esin x cos x dx = { пусть t = sin x, тогда dt = (sin x)’dx = cos x dx} =
=  etdt = et + C = esin x + C. Проверка: (esin x + C)` = esin x cos x
etdt = et + C = esin x + C. Проверка: (esin x + C)` = esin x cos x
Основной метод вычисления интегралов – поиск подходящей замены переменных. Каждому типу функций соответствует свой вид замены переменных и их надо знать.
Линейная замена: t = ax + b. Пр.  e3x dx,
e3x dx, 
 ,
,  sin (a – b x) dx
sin (a – b x) dx
Общее правило: если  f(x) dx = F(x) + C, то
f(x) dx = F(x) + C, то  f(ax + b) dx = (1/a) F(ax + b) + C, (4)
f(ax + b) dx = (1/a) F(ax + b) + C, (4)
Метод подведения под знак дифференциала - переход от u’(x) dx к du(x) (5)
Пр. 
 ,
, 
 ,
, 
 ,
, 

Случай f(x) = u`(x)/u(x). 
 dx = ln u(x) + C (6)
dx = ln u(x) + C (6)
Если числитель подынтегральной функции равен или пропорционален производной от знаменателя, то интеграл равен логарифму знаменателя.
Пр.  x dx /(x2 + 1) = ½
x dx /(x2 + 1) = ½  d(x2 + 1) / (x2 + 1) = ½ ln |x2 + 1| + C
d(x2 + 1) / (x2 + 1) = ½ ln |x2 + 1| + C
 tg x dx,
tg x dx,  ctg x dx,
ctg x dx, 
 ,
, 
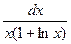
Интегрирование по частям.
Пусть u = u(x), v = v(x) -непрерывные функции, тогда d(uv) = udv + vdu.
Проинтегрируем это равенство и получим формулу интегрирования по частям.
 u dv = uv +
u dv = uv +  v du (7)
v du (7)
Она позволяет вычисление интеграла  u dv заменить на вычисление интеграла
u dv заменить на вычисление интеграла  v du.
v du.
Применение:
пусть f(x) = P(x)A(x), где P(x) = a xn + b xn-1 +...+ c, A(x) -функция другого типа.
Если A(x) = ekx, ax, sin kx, cos kx, то u = P(x), dv = A(x) dx
Если A(x) = loga x, arcsin x, arccos x, arctg x, arcctg x, то u = A(x), dv = P(x) dx
Пр.  x cos x dx = {u = x, du = dx, dv = cos x dx, v = sin x} = x sin x -
x cos x dx = {u = x, du = dx, dv = cos x dx, v = sin x} = x sin x -  sin x dx =
sin x dx =
= x sin x + cos x + C. Проверка: (x sin x + cos x + C)` = x cos x




