Насы́щенный пар — пар, находящийся в термодинамическом равновесии с жидкостью или твёрдым телом того же состава.
Давление насыщенного пара сильно зависит от температуры.
При равенстве внешнего давления давлению насыщенного пара происходит кипение (жидкости).
В определенный момент устанавливается состояние равновесия, наступает максимально возможное при данной температуре насыщение пространства над жидкостью паром. Давление, соответствующее такому равновесию, называется упругостью насыщенных паров при данной температуре, или давлением паров жидкости при данной температуре. Если резко уменьшить давление над поверхностью жидкости, то возникает интенсивное испарение с поверхности и даже во всей массе, т. е. жидкость начинает кипеть.
14. В каких единицах выражают плотность, объемный вес, коэффициенты температурного расширения и объемного сжатия, объемный модуль упругости, динамический и кинематический коэффициенты вязкости?
Если напряжение измеряется в паскалях, то, поскольку деформация является безразмерной величиной, единицей измерения модуля упругости также будет паскаль.
βv – изотермический коэффициент объёмного сжатия, м2/Н = Па-1
βt – изобарический коэффициент температурного расширения, oC-1
15. Объясните физический смысл понятий: давление жидкости в точке поверхности твердого тела, сила давления жидкости, центр тяжести плоской фигуры, центр весового давления жидкости, сила внешнего давления на поверхность твердого тела, плотность жидкости, модуль объемной упругости.
Нормальная сжимающая сила, приходящаяся на единицу площади, называется гидромеханическим давлением, а в случае покоя жидкости – гидростатическим давлением, или просто давлением и обозначается буквой P и называется давлением в точке. В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Жидкость оказывает силовое воздействие на дно и стенки сосуда.
Точку приложения суммарной силы давления называют центром давления. Центр давления всегда расположен ниже центра тяжести фигуры на расстояние J/(lω), где J – момент инерции площади фигуры, l – координата центра тяжести, ω – угл.скорость. Это расстояние называется эксцентриситетом.
П л о т н о с т ь. Плотность ρ – масса жидкости М в единице объема V. Для однородной жидкости ρ=M/V. Величина, обратная коэффициенту βp (сжимаемости - свойство капельной жидкости изменять свой объем под действием давления), представляет собой объемный модуль упругости жидкости K=1/ βp
Рабс= Рвн +Ризб
где Рабс - абсолютное давление; Рвн и Ризб – соответственно внешнее и избыточное давления.
Из уравнения следует, что при изменении внешнего давления Р0 величина Р в любой точке жидкости изменяется на такую же величину. Таким образом, внешнее давление передается без изменения во все точки внутри жидкости (закон Паскаля).
16. Что такое центр давления? Когда центр давления плоской фигуры совпадает с ее центром тяжести?
Точка приложения Д равнодействующей силы давления называется
центром давления. Координата центра давления (рис.2.7 и 2.8) определяется по формуле
(2.10)
где J0 – момент инерции площадки относительно центральной оси,
параллельной свободной поверхности, следовательно, оси X; уg, уc, hg, hc -координаты точек С и Д) соответственно по оси у и по вертикали.
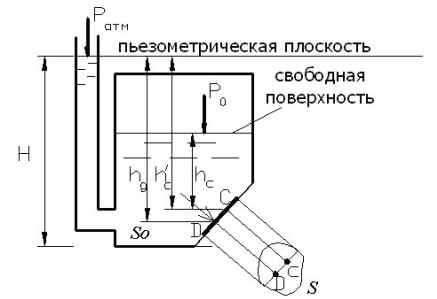
Рис.2.7
Рис.2.8
Из формулы (2,10) следует, что центр давления D расположен, как правило, ниже центра тяжести С фигуры. В случае, когда стенка горизонтальна, C и D совпадают.
17. Основные законы гидростатики: закон Гука, закон Паскаля, закон сохранения энергии (основное уравнение гидростатики), закон Архимеда.
Само существование жидких и твердых тел свидетельствует о наличии сил взаимодействия между молекулами. Эти силы определяются электромагнитными взаимодействиями между движущимися заряженными частицами, из которых состоят атомы и молекулы (электронами и ядрами). Теоретический расчет этих сил чрезвычайно сложен, и в общем виде эта задача не решена до настоящего времени. Однако, можно утверждать, что эти силы могут быть как силами притяжения (без сил притяжения все молекулы бы разлетелись из-за их теплового движения), так и силами отталкивания (без которых бы все тела сжались в одну точку). Равновесному положению молекул в жидкости и твердом теле соответствует равенство сил притяжения и отталкивания. При деформации тел (как жидких, так и твердых) равновесные расстояния между молекулами изменяются, поэтому возникают силы, стремящиеся вернуть их в исходное состояние. Эти силы проявляются как силы упругости.
Силы упругости возникают, как в твердых телах, так и в жидкостях и газах. Для жидких тел имеет смысл говорить только о нормальной силе, так как тангенциальные силы приведут к перетеканию жидкости. Вспомните: «твердые тела сохраняют свою форму и объем, а жидкости ее не сохраняют». Поэтому говорят, что в жидкостях отсутствуют тангенциальные силы упругости. Такие свойства жидкости обусловлены ее молекулярным строением: силы взаимодействия между молекулами проявляются только при изменении расстояния между молекулами, сдвиг одной молекулы относительно другой не приводит к появлению дополнительного взаимодействия. Отметим, что силы упругости жидкости могут быть направлены как внутрь, так и наружу от жидкости, то есть, жидкость может быть, как сжата, так и растянута. Так как жидкости при отсутствии внешних воздействий сохраняют свой объем, то существует равновесное расстояние между молекулами, при котором сила их взаимодействия равна нулю. При уменьшении равновесного объема расстояния между молекулами меньше равновесных, поэтому между молекулами начинают возникать силы отталкивания, в противном случае увеличения объема расстояния между молекулами превышают равновесные, поэтому начинают проявляться силы притяжения.
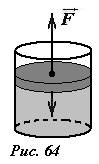
Пусть жидкость находится в сосуде под поршнем. Если к поршню приложить силу, направленную наружу от жидкости, то благодаря силам притяжения между молекулами жидкости, а также жидкости и поршня, жидкость окажется растянутой, вследствие чего, появятся силы упругости, направленные внутрь жидкости (рис. 64). Большинство жидкостей деформируются чрезвычайно мало, то есть для того, чтобы получить заметную деформацию необходимо приложить значительные внешние силы, и, наоборот – малые деформации жидкости приводят к возникновению больших сил упругости. Во многих случаях связь между деформациями и силами упругости жидкостей может считаться линейной, соответствующей закону Гука.
Основное уравнение гидростатики: P=P0+ρgh, (2.5)
где P - давление в произвольной точке на глубине h от свободной поверхности (h=Z0-Z); P0 –давление на свободной поверхности. Величина давления ρgh обусловлена весом столба жидкости высотой h. Формулу (2.5) можно переписать в виде Pабс=Рвн+Ризб,
где Рабс - абсолютное давление; Рвн и Ризб – соответственно внешнее и избыточное давления.
Из уравнения (2.5) следует, что при изменении внешнего давления Р0 величина Р в любой точке жидкости изменяется на такую же величину. Таким образом, внешнее давление передается без изменения во все точки внутри жидкости (закон Паскаля).
18. Сформулируйте условия плавания тел.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:
a. Fт>FA - тело тонет;
b. Fт=FA - тело плавает в жидкости или газе;
c. Fт<FA - тело всплывает до тех пор, пока не начнет плавать.
19. Гипотеза сплошности среды.
Рассматривать и математически описывать жидкость как совокупность огромного количества отдельных частиц, находящихся в постоянном непрогнозируемом движении, на современном уровне науки не представляется возможным. По этой причине жидкость рассматривается как некая сплошная деформируемая среда, имеющая возможность непрерывно заполнять пространство, в котором она заключена. Другими словами, под жидкостями понимают все тела, для которых характерно свойство текучести, основанное на явлении диффузии. Текучестью можно назвать способность тела как угодно сильно менять свой объём под действием сколь угодно малых сил. Таким образом, в гидравлике жидкость понимают как абстрактную среду – континуум, который является основой гипотезы сплошности. Континуум считается непрерывной средой без пустот и промежутков, свойства которой одинаковы во всех направлениях. Это означает, что все характеристики жидкости являются непрерывными функциями и все частные производные по всем переменным также непрерывны.
По-другому такие тела (среды) называют капельными жидкостями. Капельные жидкости - это такие, которые в малых количествах стремятся принять шарообразную форму, а в больших образуют свободную поверхность.
Сплошная среда представляет собой модель, которая успешно используется при исследовании закономерностей покоя и движения жидкости. Правомерность применения такой модели жидкости подтверждена всей практикой гидравлики.
Изучение реальных жидкостей и газов связано со значительными трудностями, т.к. физические свойства реальных жидкостей зависят от их состава, от различных компонентов, которые могут образовывать с жидкостью различные смеси как гомогенные (растворы) так и гетерогенные (эмульсии, суспензии и др.) По этой причине для вывода основных уравнений движения жидкости приходится пользоваться некоторыми абстрактными моделями жидкостей и газов, которые наделяются свойствами неприсущими природным жидкостям и газам.
21. Силы, действующие на частицы в сплошной среде: массовые и поверхностные силы.
Массовыми называют силы, величина которых пропорциональна массе жидкости. Они приложены ко всякой материальной частице М рассматриваемого объема. К ним относятся силы тяжести и силы инерции.
Поверхностными силами называют силы, величина которых пропорциональна площади поверхности выделенного объема жидкости. Это те силы, которые действуют на поверхность рассматриваемого объема со стороны окружающей его жидкости или твердых тел. Поверхностные силы, по отношению к рассматриваемому объему являются внешними.
22. Как определить силу давления жидкости на плоскую поверхность твердого тела (модуль, направление, точку приложения)?
По этим формулам определяются координаты точки приложения силы давления.
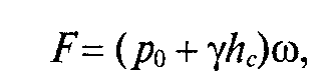формула для определения силы давления на плоскую поверхность. Сила давления направлена перпендикулярно поверхности на которую она давит.
23. Ньютоновские и неньютоновские жидкости.
Закон Ньютона для внутреннего трения в жидкости гласит, что при отсутствии относительной скорости движения слоев сила трения отсутствует и что сила трения не зависит от относительной скорости перемещения слоев. Жидкости которые подчиняются данному закону называют Ньютоновскими.
Неньютоновские жидкости представляют собой различные эмульсии и коллоидные растворы, которые состоят из двух фаз (твердой и жидкой)
24. Идеальная и вязкая жидкости.
Идеальная жидкость характеризуется абсолютной подвижностью, т.е. отсутствием сил взаимодействия между молекулами и абсолютной неизменяемостью в объеме при изменении температуры или под действием каких-либо сил. Идеальная жидкость не сопротивляется сдвигающим усилиям. Реальная или вязкая жидкость наоборот.
25. Гидравлические характеристики потока. Расход и средняя скорость.
Гидравлические характеристики потока – это давление и скорость.
Объемным расходом называется объем жидкости проходящий через данное сечение в единицу времени. Объемный расход определяется по формуле: 
Средняя скорость в сечении потока – это такая скорость, одинаковая для всех точек сечения потока, при которой происходит тот же расход, какой фактически имеет место при действительных скоростях, различных точек сечения. Средняя скорость определяется по формуле:
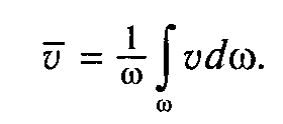
Также средняя скорость равна половине максимальной скорости потока:
26. Поток как совокупность элементарных струек. Понятие о линии тока и элементарной струйке.
В гидравлике применяется струйчатая модель движения жидкости. Поток жидкости рассматривается как состоящий из отдельных элементарных струек.
Линия тока - линия, проведенная в данный момент времени в движущейся жидкости так, что в любой ее точке вектор скорости частиц совпадает с касательной (рис.2.ІІ).При установившемся движении линия
тока совпадает с траекторией частиц.
Элементарная струйка – совокупность линий тока, проведенных через все точки элементраной площадки.
27. Уравнение Бернулли для потока реальной жидкости. Что представляет собой коэффициент α и что он учитывает?
Уравнение Бернулли для потока имеет вид:
a - коэффициент кинематической энергии потока(коэффициент кориолиса). Отношение кинетической энергии потока к кинетической энергии, вычисленной в предположении что скорости всех точек живого сечения потока равны соедней скорости потока т.е.
Отсюда заключаем, что a характеризует неравномерность распределения скоростей по сечению потока. Для ламинарного около 2, для турбулентного a=1,05-1.1
28. Как определить положение пьезометрической плоскости при известной величине избыточного давления над свободной поверхностью жидкости?
Сила избыточного давления над свободной поверхностью равно:
Где hc – расстояние от центра тяжести до пьезометрической плоскости,
S- площадь поверхности.
F=Po*S.
