ВАРИАНТ №1
Задание №1 Решить систему линейных уравнений тремя методами:
· методом Гаусса.
· по формулам Крамера, 
· методом обратной матрицы.
Задание №2 Найти общее решение системы линейных уравнений методом Гаусса
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (2,3); В (1,3); С (-6,-4).
Задание №4 Построить кривые по заданным уравнениям
а) (х – 2)2 + (у – 3)2 = 9; в) 
;
б)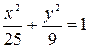 
; г) у2 = 9х.
ВАРИАНТ №2
Задание №1 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 
· методом обратной матрицы.
Задание №2 Найти общее решение системы линейных уравнений методом Гаусса
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (1,1); В (-3,3); С (-5,-2).
Задание №4 Построить кривые по заданным уравнениям
а) (х + 3)2 + (у – 5)2 = 4; в) 
;
б) 
; г) у2 = 7х.
ВАРИАНТ №3
Задание №1 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 
· методом обратной матрицы.
Задание №2 Найти общее решение системы линейных уравнений методом Гаусса
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (1,2); В (-2,3); С (-2,-3).
Задание №4 Построить кривые по заданным уравнениям
а) (х + 1)2 + (у – 2)2 = 16; в) 
;
б) 
; г) у2 = 5х.
ВАРИАНТ №4
Задание №1 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 
· методом обратной матрицы.
Задание №2 Найти общее решение системы линейных уравнений методом Гаусса
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (2,1); В (-3,2); С (-1,-4).
Задание №4 Построить кривые по заданным уравнениям
а) (х − 3)2 + (у + 4)2 = 25; в) 
;
б) 
; г) у2 = 16х.
ВАРИАНТ №5
Задание №1 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 
· методом обратной матрицы.
Задание №2 Найти общее решение системы линейных уравнений методом Гаусса
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (1,3); В (-2,2); С (-3,-5).
Задание №4 Построить кривые по заданным уравнениям
а) (х + 3)2 + (у + 3)2 = 4; в) 
;
б) 
; г) у2 = 3х.
ВАРИАНТ №6
Задание №1 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 
· методом обратной матрицы.
Задание №2 Найти общее решение системы линейных уравнений методом Гаусса
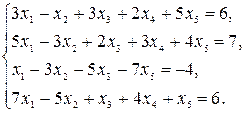
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (3,1); В (-3,1); С (2,-3).
Задание №4 Построить кривые по заданным уравнениям
а) (х − 1)2 + (у + 2)2 = 1; в) 
;
б)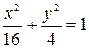 
; г) у2 = 4х.
ВАРИАНТ №7
Задание №1 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 
· методом обратной матрицы.
Задание №2 Найти общее решение системы линейных уравнений методом Гаусса
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (2,2); В (-1,3); С (0,-5).
Задание №4 Построить кривые по заданным уравнениям
а) (х − 3)2 + (у – 2)2 = 9; в) 
;
б) 
; г) у2 = -4х.
ВАРИАНТ №8
Задание №1 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 
· методом обратной матрицы.
Задание №2 Найти общее решение системы линейных уравнений методом Гаусса
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (3,2); В (-2,1); С (-5,-5).
Задание №4 Построить кривые по заданным уравнениям
а) (х − 5)2 + (у + 3)2 = 4; в) 
;
б) 
; г) у2 = -2х.
ВАРИАНТ №9
Задание №1 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 
· методом обратной матрицы.
Задание №2 Найти общее решение системы линейных уравнений методом Гаусса
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (2,3); В (-1,2); С (-4,-4).
Задание №4 Построить кривые по заданным уравнениям
а) (х + 1)2 + (у + 1)2 = 16; в) 
;
б) 
; г) у2 = -6х.
ВАРИАНТ №10
Задание №1 Решить систему линейных уравнений тремя методами:
· методом Гаусса,
· по формулам Крамера, 
· методом обратной матрицы.
Задание №2 Найти общее решение системы линейных уравнений методом Гаусса
Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
· площадь треугольника АВС,
· точку М, симметричную точке А относительно стороны ВС,
· уравнение медианы ВК.
А (3,3); В (-1,1); С (0,-7).
Задание №4 Построить кривые по заданным уравнениям
а) (х + 4)2 + (у – 3)2 = 25; в) 
;
б) 
; г) у2 = -х.
ВОПРОСЫ К ЭКЗАМЕНУ
1. Основные понятия о матрицах.
2. Операции над матрицами.
3. Определители квадратных матриц.
4. Свойства определителей.
5. Обратная матрица.
6. Ранг матрицы.
7. Основные понятия системы линейных уравнений.
8. Метод обратной матрицы.
9. Метод Крамера.
10. Метод Гаусса.
11. Уравнение линии на плоскости.
12. Уравнение прямой.
13. Условия параллельности и перпендикулярности прямых. Расстояние от точки до прямой.
14. Понятие функции. Основные свойства функций.
15. Предел числовой последовательности.
16. Предел функции в бесконечности и в точке.
17. Бесконечно малые величины и их свойства.
18. Бесконечно большие величины.
19. Основные теоремы о пределах.
20. Замечательные пределы.
21. Непрерывность функции.
22. Определение производной. Основные правила дифференцирования.
23. Производная сложной функции.
24. Основные теоремы дифференциального исчисления.
25. Правило Лопиталя.
26. Возрастание и убывание функции.
27. Экстремум функции.
28. Наибольшее и наименьшее значение функции на отрезке.
29. Выпуклость функции. Точки перегиба.
30. Асимптоты графика функции.
31. Понятие дифференциала функции.
32. Частные производные первого порядка.
33. Частные производные высших порядков.
34. Экстремумы функций двух переменных.
35. Условный экстремум.
36. Метод наименьших квадратов.
РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ
1. Кремер, Н.Ш. Практикум по высшей математике для экономистов / / Н.Ш.Кремер – М.: ЮНИТИ-ДАНА, 2002.
2. Кремер, Н.Ш. Высшая математика для экономистов / Н.Ш.Кремер – М.: Банки и биржи, ЮНИТИ, 2009.
3. Математический анализ и линейная алгебра. Учебное–методическое пособие. / Под ред. Н.Ш.Кремера - М.: ВЗФЭИ, 2002.
