Математика: Методические рекомендации по выполнению домашней контрольной работы / Е.А.Сбродова - Челябинск: ЧОУ ВПО Южно-Уральский институт управления и экономики, 2014.- 21с.
Математика: Методические рекомендации по выполнению домашней контрольной работы: 080200.62 «Менеджмент»
Ó Издательство ЧОУ Южно-Уральский институт управления и экономики», 2014
СОДЕРЖАНИЕ
| Введение…………………………………………………………………… | |
| Методические рекомендации по выполнению контрольных заданий… | |
| Задания для домашней контрольной работы…………………………… | |
| Рекомендуемый список литературы…………………………………….. |
ВВЕДЕНИЕ
Цель курса математики в системе подготовки экономиста– освоение необходимого математического аппарата.
Это необходимо для анализа моделирования и решения прикладных экономических задач, в том числе с использованием ЭВМ.
Задачи изучения математики как фундаментальной дисциплины состоят в развитии логического и алгоритмического мышления, в выработке умения моделировать реальные экономические процессы.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ
РАЗДЕЛ 1 ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Тема 1 Матрицы и определители
Определение матрицы. Виды матриц. Транспонирование матриц. Алгебраические операции над матрицами. Определители второго, третьего порядков и матрицы n-го порядка. Теорема Лапласа. Присоединенная и обратная матрицы. Алгоритм вычисления обратной матрицы. Ранг матрицы как наивысший порядок ее миноров, отличных от нуля. Вычисление ранга матрицы с помощью элементарных преобразований. Линейная комбинация, линейная зависимость и независимость строк (столбцов) матрицы. Теорема о ранге матрицы — максимальном числе ее линейно независимых строк (столбцов). (1, гл.1, § 1.1-1.6; с.9-35); (2, гл.1).
Надо хорошо уяснить, что матрица — это прямоугольная таблица,составленная из mn чисел, расположенных в m строках и n столбцах. Необходимо знать, как устанавливаются размеры матрицы и ее порядок, уметь выполнять транспонирование матриц, алгебраические операции над ними (умножение матрицы на число, сложение, вычитание, умножение матриц).
Необходимо усвоить следующее: строки обозначаются индексом ”i”, столбцы индексом ”j”. Поэтому любой элемент матрицы можно обозначить aij. Это означает, что элемент aij находится в i-ой строке и в j-ом столбце. Например, a11 – элемент первой строки и первого столбца; a23–элемент второй строки и третьего столбца. Индекс с «i» растет всегда «вниз», а индекс «j» – растет вправо.
Размер матрицы m х n означает, что конечные величины i и j равны соответственно m и n, т.е. iкон=m, jкон=n.
При вычислении определителей необходимо отметить, что определитель есть число и вычисляется по определенным правилам. Необходимо рассмотреть правило вычисления определителей второго порядка и правило треугольника или правило Сарруса для вычисления определителей третьего порядка.
В качестве универсального метода вычисления определителей необходимо рекомендовать вычисление на основе теоремы Лапласа.
Для этого нужно знать определение минора (вычисление), определение алгебраического дополнения Aij=(-1)i+jMij и саму теорему Лапласа. (1, пример 9, с. 25, с. 26).
Мало того, нужно обратить внимание и на то, что определители порядка больше трех вычисляются с помощью теоремы Лапласа.
Относительные трудности возникают при усвоении операции умножения матриц. Необходимо твердо усвоить формальное правило умножения (1, с. 12 – 13) и связанное с ним условие существования произведения АВ матриц А и В:число столбцов матрицы А должно быть равно числу строк матрицы В. Одна из особенностей операции умножения состоит в том, что произведение матриц в общем случае не коммутативно, т.е. АВ ¹ ВА. Даже если А и В – квадратные матрицы, в общем случае АВ ¹ ВА, в чем нетрудно убедиться на любом частном примере. Другая особенность произведения матриц состоит в том, что произведение двух ненулевых матриц может оказаться нулевой матрицей.
Например, можно легко показать, что произведение матриц есть нулевая матрица (сравните: во множестве действительных чисел произведение равно нулю тогда, когда хотя бы один из сомножителей равен нулю).
= 
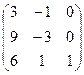
Нужно знать определение присоединенной и обратной матриц, уметь их вычислять, знать, что для существования матрицы А-1, обратной матрице А, необходимо и достаточно, чтобы матрица А была невырожденной (неособенной). Проверить правильность вычисления обратной матрицы можно, составив произведение АА-1 или А-1 А. Если оно является единичной матрицей Е, то, в соответствии с определением, матрица А -1 вычислена правильно.
Нужно уметь вычислять определители второго и третьего порядков (метод треугольника) и более высших порядков (1, пример 1.9, c.25, 26). При вычислении определителей нужно активно использовать свойства определителей 2,4,5,6,8. Теорему Лапласа нужно знать твердо и уметь ее использовать для практики.
Разобрать для усвоения материала по вычислению определителей задачи 1.19-1.21.
Вычисление обратной матрицы осуществлять по алгоритму, изложенному в (1). Нужно четко усвоить в алгоритме, что обратная к исходной матрице существует. После этого определяется транспонированная к исходной матрица. Именно для транспонированной матрицы А¢ ищутся алгебраические дополнения Aij.
Из алгебраических дополнений к транспонированной матрице составляется присоединенная (союзная) матрица.
Если известна союзная матрица 
и определитель 
исходной матрицы, то вычисляется обратная матрица
A-1= / .
Обратная матрица будет использоваться для решения систем линейных уравнений.
Для усвоения материала необходимо разобрать задачи (1, 1.15— 1.18, 1.22—1.29).
Пример: Найти матрицу С=В¢×А¢×А×В, если А= 
, В= 
.
Решение:
Алгоритм решения:
1. Находим матрицы В¢, А¢, транспонированные к матрицам А и В.
А¢= 
, В¢= 
.
2. Находим произведение матриц:
В¢×А¢= × = 
.
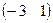Это возможно ибо число столбцов матрицы В¢ равно числу строк матрицы А¢.
3. Находим произведение матриц:
А×В= = 
.
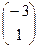4. Находим произведение
С=В¢×А¢×А×В= 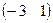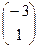= (10)
Ответ: C = (10)
