Общее уравнение прямой. Частные случаи общего уравнения прямой.

Общее уравнение прямой:

Ax + By + C = 0

 

Частные случаи общего уравнения прямой:

а) Если C = 0, уравнение (2) будет иметь вид

Ax + By = 0,

и прямая, определяемая этим уравнением, проходит через начало координат, так как координаты начала координат x = 0, y = 0 удовлетворяют этому уравнению.

б) Если в общем уравнении прямой (2) B = 0, то уравнение примет вид

Ax + С = 0, или .

Уравнение не содержит переменной y, а определяемая этим уравнением прямая параллельна оси Oy.

в) Если в общем уравнении прямой (2) A = 0, то это уравнение примет вид

By + С = 0, или ;

уравнение не содержит переменной x, а определяемая им прямая параллельна оси Ox.

Следует запомнить: если прямая параллельна какой-нибудь координатной оси, то в ее уравнении отсутствует член, содержащий координату, одноименную с этой осью.

г) При C = 0 и A = 0 уравнение (2) принимает вид By = 0, или y = 0.

Это уравнение оси Ox.

д) При C = 0 и B = 0 уравнение (2) запишется в виде Ax = 0 или x = 0.

Это уравнение оси Oy.

Взаимное расположение прямых на плоскости. Угол между прямыми на плоскости. Условие параллельности прямых. Условие перпендикулярности прямых.

l₁ l₂ l₁: A₁x + B₁y + C₁ = 0
l₂: A₂x + B₂y + C₂ = 0

S₂ S₁ Вектора S₁ и S₂ называются направляющими для своих прямых.

 

 

Угол между прямыми l₁ и l₂ определяется углом между направляющими векторами.
Теорема 1: cos угла между l₁ и l₂ = cos(l₁ ; l₂) =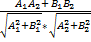

Теорема 2: Для того, чтобы 2 прямые были равны необходимо и достаточно:

l₁ = l₂ ó

 

Теорема 3: чтобы 2 прямые были перпендикулярны необходимо и достаточно:

l₁ l₂ ó A₁A₂ + B₁B₂ = 0

Вопрос 13

Общее уравнение плоскости и его частные случаи. Уравнение плоскости в отрезках.

Общее уравнение плоскости:

Ax + By + Cz + D = 0

Частные случаи:

1. D=0 Ax+By+Cz = 0 – плоскость проходит через начало координат

2. С=0 Ax+By+D = 0 – плоскость || OZ

3. В=0 Ax+Cz+d = 0 – плоскость || OY

4. A=0 By+Cz+D = 0 – плоскость || OX

5. A=0 и D=0 By+Cz = 0 – плоскость проходит через OX

6. В=0 и D=0 Ax+Cz = 0 – плоскость проходит через OY

7. C=0 и D=0 Ax+By = 0 – плоскость проходит через OZ

Взаимное расположение плоскостей и прямых линий в пространстве:

1. Углом между прямыми в пространстве называется угол между их направляющими векторами.

Cos (l₁; l₂) = cos(S₁; S₂) = =

2. Углом между плоскостями определяется через угол между их нормальными векторами.

Cos (l₁; l₂) = cos(N₁; N₂) = =

3. Косинус угла между прямой и плоскостью можно найти через sin угла между направляющим вектором прямой и нормальным вектором плоскости.

4. 2 прямые || в пространстве, когда их || направляющие вектора

5. 2 плоскости || когда || нормальные вектора

6. Аналогично вводятся понятия перпендикулярности прямых и плоскостей.

 

 

Вопрос №14

Различные виды уравнения прямой линии на плоскости(уравнение прямой в отрезках, с угловым коэффициентом и др.)

Уравнение прямой в отрезках:
Допустим, что в общем уравнении прямой:

1. С = 0 Ах + Ву = 0 – прямая проходит через начало координат.

2. а = 0 Ву + С = 0 у =

3. в = 0 Ах + С = 0 х =

4. в=С=0 Ах = 0 х = 0

5. а=С=0 Ву = 0 у = 0

 

Уравнение прямой с угловым коэффициентом:

Любая прямая, не равная оси ОУ (В не=0), может быть записана в след. виде:

у = kx + b

k = tgα α – угол между прямой и положительно направленной линией ОХ

b – точка пересечения прямой с осью ОУ

 

Док-во:

Ах+Ву+С = 0

Ву= -Ах-С |:В

 

У =

 

У = kx + b

Уравнение прямой по двум точкам:

Вопрос №16

Конечный предел функции в точке и при x→∞

Конечный предел в точке х₀:

Число А называется пределом функции y = f(x) при x→х­_0­, если для любого Е > 0 существует б > 0 такое, что при х ≠x₀, удовлетворяющее неравенству |х – х₀| < б, выполняется условие |f(x) - A| < Е

 

Предел обозначается: = A

 

Конечный предел в точке +∞:

Число А называется пределом функции y = f(x) при x → ₊ ∞, если для любого Е > 0 существует С > 0, такое что при x > C выполняется неравенство |f(x) - A| < Е

 

Предел обозначается: = A

 

Конечный предел в точке -∞:

Число А называется пределом функции y = f(x) при x→-∞, если для любого Е < 0 существует С < 0 такое, что при х < -С выполняется неравенство |f(x) - A| < Е

 

Предел обозначается: = A

 

Общее определение конечного предела:

Число А называется пределом функции y = f(x) при x→x₀, если для любого Е > 0 существует б > 0 такое, что х принадл. тогда f(x) принадл. (А)