Стратегия решения задачи состоит в построении последовательности точек, k=0, 1, 2,... n таких, что, 
k=0,1,2,...n. Точки последовательности вычисляются по правилу: 
k=0,1,2,...В качестве начала итераций выбирается произвольная точка. Величина шага задается пользователем и остается постоянной до тех пор, пока функция убывает в точках последовательности, т.е. до тех пор, пока выполняется соотношение 
. Если это условие не выполняется, то производится коррекция длины шага, и опять проверяется выполнение неравенства. Процесс завершается в точке, для которой выполняется условие окончания - 
.
Метод наискорейшего градиентного спуска
Градиентный спуск — метод нахождения локального минимума функции с помощью движения вдоль градиента. Для минимизации функции в направлении градиента используются методы одномерной оптимизации, например, метод золотого сечения. Стратегия решения задачи состоит в построении такой последовательности точек, что значение функции в каждой последующей точке меньше чем в предыдущей. Точки последовательности вычисляются по правилу 
где величина шага tk определяется для каждого значения k из условия
.
Аналитическое решение уравнений
Решим заданные уравнения аналитическим способом.
1) 
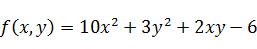
Найдем первые частные производные:
; 
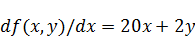Прировняем полученные производные к нулю и найдем корни системы уравнений:
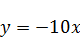
Искомое решение уравнения: 
;
Значение функции в найденной точке: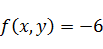 
2) 
Найдем первые частные производные:
; 
Прировняем полученные производные к нулю и найдем корни уравнения:
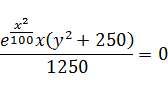
0 
Искомое решение уравнения: ;
Значение функции в найденной точке: 
Исследование работы реализованных методов
Симплекс-метод
Рассмотрим работу программы при различных входных данных.
В качестве рассматриваемой функции выберем
,
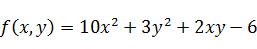имеющую решение в точке .
Зададим исходные данные:
| A | B | C | 
| 
| 
| 
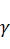
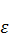
| N |
| (9; 9) | (6; 8) | (9; 6) | 0,5 | 0,001 |
Окно программы при решении симплекс-методом с заданными параметрами – рисунок 3.
Рисунок 2
Вариации с коэффициентом отражения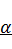 
Увеличим коэффициент :
| A | B | C |
|
|
|
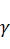
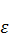
| N |
| (9; 9) | (6; 8) | (9; 6) | 0,5 | 0,001 |
Решение при новых параметрах – рисунок 4.
Рисунок 4
Уменьшим коэффициент :
| A | B | C |
|
|
|
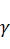
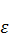
| N |
| (9; 9) | (6; 8) | (9; 6) | 0,5 | 0,5 | 0,001 |
Решение при новых параметрах – рисунок 5.
Рисунок 5
Вариации с коэффициентом сжатия 
Восстановим исходные параметры – рисунок 3.
Зададим коэффициент сжатия 
и повторим расчет.
| A | B | C |
|
|
|
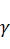
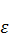
| N |
| (9; 9) | (6; 8) | (9; 6) | 0,8 | 0,001 |
Решение при новых параметрах – рисунок 6.
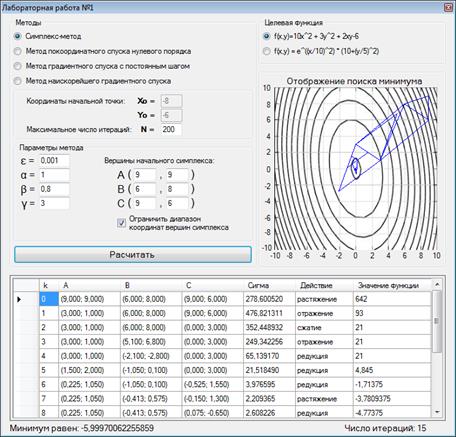
Рисунок 6
Уменьшим коэффициент сжатия 
:
| A | B | C |
|
|
|
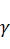
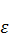
| N |
| (9; 9) | (6; 8) | (9; 6) | 0,2 | 0,001 |
Решение при новых параметрах – рисунок 7.
Рисунок 7
Вариации с коэффициентом растяжения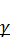 
Восстановим исходные параметры – рисунок 3.
Зададим коэффициент растяжения 
и повторим расчет.
| A | B | C |
|
|
|
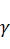
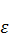
| N |
| (9; 9) | (6; 8) | (9; 6) | 0,5 | 3,5 | 0,001 |
Решение при новых параметрах – рисунок 8.
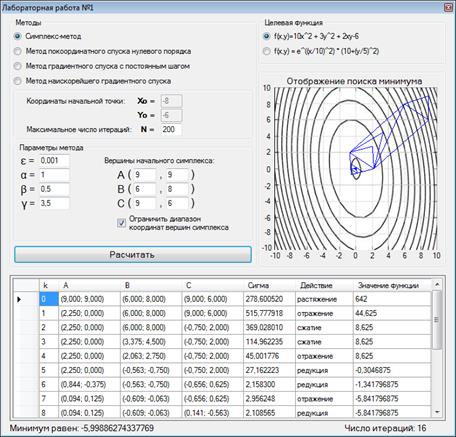
Рисунок 8
Уменьшим коэффициент растяжения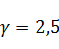 
:
| A | B | C |
|
|
|
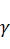
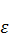
| N |
| (9; 9) | (6; 8) | (9; 6) | 0,5 | 2,5 | 0,001 |
Решение при новых параметрах – рисунок 9.
Рисунок 9
Можно сделать вывод, что применяя симплекс-метод для данной функции для получения наиболее точного решения, необходимо:
1) Задать коэффициент отражения в диапазоне [1; 2];
2) Задать коэффициент сжатия в диапазоне [0,5; 0,9];
3) Задать коэффициент растяжения в диапазоне [1; 1,9];
Также для уменьшения количества итераций необходимо:
1) Задать коэффициент отражения в диапазоне [0,8; 1];
2) Задать коэффициент сжатия в диапазоне [0,5; 0,8];
3) Задать коэффициент растяжения в диапазоне [1,8; 2;9]
.
В качестве рассматриваемой функции выберем
,
имеющую решение в точке .
Зададим исходные данные:
| A | B | C |
|
|
|
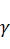
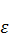
| N |
| (9; 9) | (6; 8) | (9; 6) | 0,5 | 0,001 |
Окно программы при решении симплекс-методом с заданными параметрами – рисунок 10.
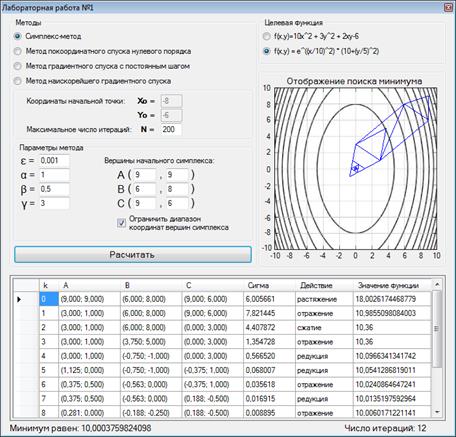
Рисунок 10
Вариации с коэффициентом отражения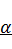
Увеличим коэффициент :
| A | B | C |
|
|
|
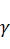
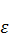
| N |
| (9; 9) | (6; 8) | (9; 6) | 0,5 | 0,001 |
Решение при новых параметрах – рисунок 11.
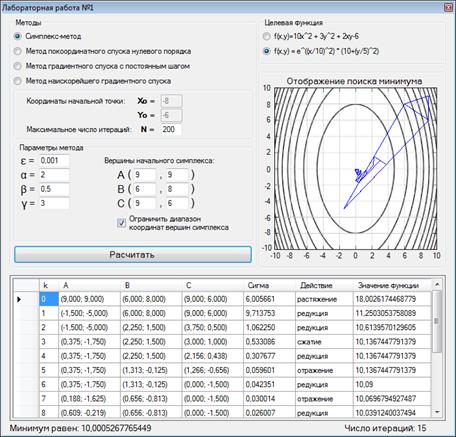
Рисунок 11
Уменьшим коэффициент :
| A | B | C |
|
|
|
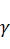
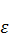
| N |
| (9; 9) | (6; 8) | (9; 6) | 0,5 | 0,5 | 0,001 |
Решение при новых параметрах – рисунок 12.
Рисунок 12
Вариации с коэффициентом сжатия
Восстановим исходные параметры – рисунок 10.
Зададим коэффициент сжатия и повторим расчет.
| A | B | C |
|
|
|
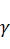
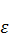
| N |
| (9; 9) | (6; 8) | (9; 6) | 0,8 | 0,001 |
Решение при новых параметрах – рисунок 13.
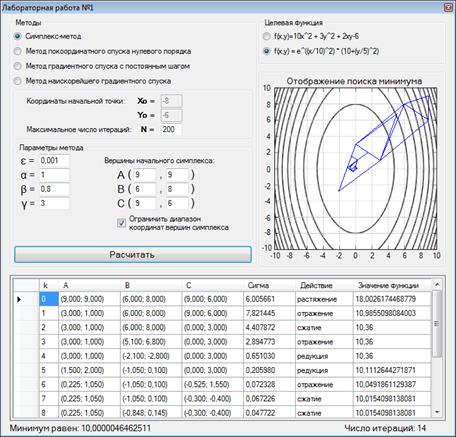
Рисунок 13
Уменьшим коэффициент сжатия :
| A | B | C |
|
|
|
| N |
| (9; 9) | (6; 8) | (9; 6) | 0,2 | 0,001 |
Решение при новых параметрах – рисунок 14.
Рисунок 14
Вариации с коэффициентом растяжения
Восстановим исходные параметры – рисунок 10.
Зададим коэффициент растяжения и повторим расчет.
| A | B | C |
|
|
|
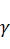
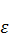
| N |
| (9; 9) | (6; 8) | (9; 6) | 0,5 | 3,5 | 0,001 |
Решение при новых параметрах – рисунок 15.
Рисунок 15
Уменьшим коэффициент растяжения :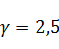
| A | B | C |
|
|
|
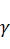
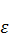
| N |
| (9; 9) | (6; 8) | (9; 6) | 0,5 | 2,5 | 0,001 |
Решение при новых параметрах – рисунок 16.
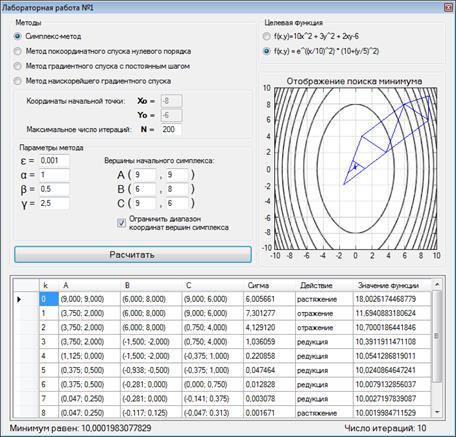
Рисунок 16
Можно сделать вывод, что применяя симплекс-метод для данной функции для получения наиболее точного решения, необходимо:
1) Задать коэффициент отражения в диапазоне [0,5; 1];
2) Задать коэффициент сжатия в диапазоне [0,5; 0,9];
3) Задать коэффициент растяжения в диапазоне [2,5; 3].
Также для уменьшения количества итераций необходимо:
1) Задать коэффициент отражения в диапазоне [0,8; 1];
2) Задать коэффициент сжатия в диапазоне [0,1; 0,7];
3) Задать коэффициент растяжения в диапазоне [2; 3,4].
Если необходимо добиться максимальной точности от данного метода, то требуется в дополнение к условиям получения наиболее точного решения, которые описаны выше, добавить ещё одно – задать максимально маленьким число 
для остановки алгоритма.
1) При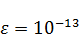 
для функции 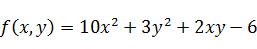получим результат (рисунок 17)
Рисунок 17
2) При 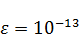для функции получим результат (рисунок 18).
Рисунок 18
