Постановка задачи
Даны две двумерные функции:
;
;
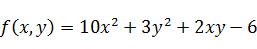1 Симплекс-метод
Дано: Координаты трех вершин начального симплекса (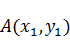
, 
, 
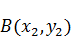), число 
для остановки алгоритма, коэффициенты отражения 
, сжатия 
и растяжения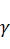 
, максимальное число итераций N.
Необходимо найти безусловный минимум функции двух переменных, т. е. найти такую точку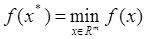 
, с помощью симплекс-метода.
Реализовать и исследовать свойства данного метода.
2 Метод покоординатного спуска нулевого порядка
Дано: начальные точки 
, 
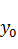, число для остановки алгоритма и максимальное число итераций N.
Необходимо найти безусловный минимум функции двух переменных, т. е. найти такую точку 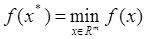, с помощью метода покоординатного спуска нулевого порядка.
Реализовать и исследовать свойства данного метода.
3 Метод градиентного спуска с постоянным шагом
Дано: начальные точки , , 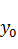малые числа 
для остановки алгоритма, N – предельное число итераций, 
– шаг.
Необходимо найти локальный минимум функции двух переменных на множестве допустимых решений, т. е. найти такую точку 
, что 
с помощью метода градиентного спуска с постоянным шагом.
Реализовать и исследовать свойства данного метода.
4 Метод наискорейшего градиентного спуска
Дано: начальные точки , , 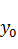малые числа для остановки алгоритма, М – предельное число итераций.
Необходимо найти локальный минимум функции двух переменных на множестве допустимых решений, т. е. найти такую точку , что с помощью метода градиентного спуска с постоянным шагом.
Реализовать и исследовать свойства данного метода.
Теоретические сведения
Симплекс-метод
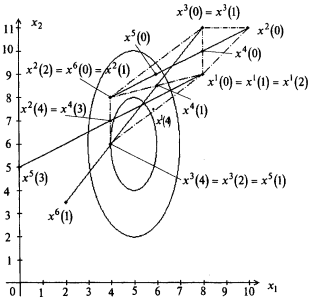В основу метода деформируемого многогранника (метода Нелдера-Мида) положено построение последовательности систем n+1 точек 
, которые являются вершинами выпуклого многогранника. Точки системы 
на 
итерации совпадают с точками системы , кроме 
, где точка 
– наихудшая в системе , т. е.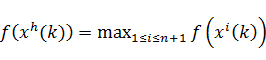 
. Точка 
заменяется на другую точку по специальным правилам. В результате многогранники деформируются в зависимости от структуры линий уровня целевой функции, вытягиваясь вдоль длинных наклонных плоскостей, изменяя направление в изогнутых впадинах и сжимаясь в окрестности минимума. Построение последовательности многогранников заканчивается, когда значение функции в вершинах текущего многогранника отличаются от значения функции в центре тяжести системы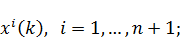 
не более чем на .
Метод покоординатного спуска нулевого порядка
Метод покоординатного спуска нулевого порядка является классическим итерационным методом решения системы линейных уравнений. Стратегия решения задачи состоит в построении такой последовательности точек, что значение функции в каждой последующей точке меньше чем в предыдущей. Точки последовательности вычисляются по следующему правилу: фиксируется одна из переменных, затем минимизируя получившуюся функцию получаем значения для второй переменной, шаг повторяется пока не достигается заданная точность.
