Физический смысл гидродинамической характеристики (ГДХ) в данной скважине получить заданный дебит.
Очевидно, что напор, необходимый для подъема заданного дебита должен поднимать жидкость с динамического уровня скважины и кроме того, создавать буферное давление.
, (7)
де dP(l) – градиент давления на глубине l с учетом зенитного угла, Па/м (в соответствии с разделом 3);
где Pбуф - буферное (устьевое) давление, Па;
Pпр – давление на приеме, Па;
rж(l) - плотность жидкости на глубине l, кг/м3;
g - ускорение свободного падения, м/с2;
L – глубина подвески установки, м;
Для того, чтобы построить ГДХ скважины, достаточно найти три ее точки. Если определить максимальный дебит скважины как дебит при котором забойное давление равно 0,7 от давления насыщения (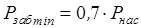
), т.е. 
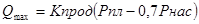, то эти три точки соответственно равны: Q1 = 0,5· Qmax, Q2 = Qmax, Q3 = 1,05·Qmax. H1, H2, H3 находят из формулы (7).
Решение системы "скважина - насосная установка"
Если построить на одном графике ГДХ скважины и рабочий участок напорной характеристики УЭЦН, то становится видно, что решением системы "скважина - насосная установка" является пересечение этих двух кривых. Если же ГДХ скважины не пересекается с рабочим участком напорной характеристики УЭЦН, то данный типоразмер установки не будет работать в оптимальном режиме, т.е. решение системы отсутствует.
Таким образом можно найти решение системы для всех интересующих типоразмеров УЭЦН и выбрать лучший (с точки зрения максимального КПД или максимального дебита) вариант.
Рисунок 5.4 Графическое решение системы "скважина - УЭЦН"
На рисунке 5.4 показан пример графического решения системы "скважина - насосная установка".
Из пересечения кривых определяем дебит Q и H для установки. Это можно сделать не только графическим, но и аналитическим методом. Для аналитического решения необходимо аппроксимировать кривые полиномами с помощью сплайн-интерполяции (для случая, когда кривые построены по 3-м точкам - параболами, т.е. полиномами 2-й степени) и найти их пресечение аналитически (для двух парабол достаточно решить квадратное уравнение).
Аналитическое решение системы «скважина-УЭЦН» возможно численным методом. Решается система из уравнений (6) и (7). При этом итеративно подбирается глубина подвески, затем определяется забойное давление (в соответствии с разделом3), дебит скважины 
. В результате находим глубину подвески, соответствующую оптимальному давлению на приеме (согласно системы уравнений 1). Далее проверяем кривизну ствола скважины на данной глубине. Если она превышает норматив 3 мин на 10 м, производим увеличение глубины с шагом инклинометрии до тех пор пока не обнаружится участок, соответствующий нормативу кривизны. В том случае если такого участка не существует выбирается участок с наименьшей кривизной.
При этом ограничениями при подборе являются: 1) забойное давление меньше 0,7 давления насыщения; 2) не возможно достичь оптимального давления на приеме; 3) расчетный подача не попадает в рабочую область напорной характеристики УЭЦН.
Таким образом осуществляется подбор типоразмера УЭЦН и расчет его основных технологических характеристик: давления на приеме, глубины подвески, дебита.
