Алгоритмы генерации случайных чисел. Алгоритм аддитивного конгруэнтного генератора псевдослучайной последовательности.

 

Простейшие алгоритмы генерации псевдослучайных последовательностей

Очень широко генераторы псевдослучайных чисел используются во многих программных приложениях от конструирования ядерных реакторов и радиолокационных систем раннего обнаружения до поисков нефти и многоканальной связи.

Использование стандартных функций языков высокого уровня

Функция Rand() выдает псевдослучайное число в указанном диапазоне (способ задания диапазона отличается в различных языках). Начальная инициализация генератора случайных чисел происходит при помощи системного вызова специальной функции. Для C – это функция srand, а для Object Pascal задание начального значения реализовано через свойство RandSeed, в Basic – randomaze.

Все эти функции генерируют псевдослучайные числа в указанном диапазоне.

Генерация псевдослучайных последовательностей (ПСП) давно занимала математиков и одним из первых способов было предложено получать их как значения дробной части многочлена первой степени:

Y_n = Ent (a∙n+b), где Ent – дробная часть полученного выражения.

Если n пробегает значения натурального ряда чисел, то поведение Y_n выглядит весьма хаотичным. Еще Карл Якоби доказал, что при рациональном коэффициенте а множество { Y_n } конечно, а при иррациональном – бесконечно и всюду плотно в интервале от 0 до 1.

Однако эти результаты далеки от практики получения псевдослучайных рядов чисел. Дело в том, что теорема Якоби относится к действительным числам, которые не могут быть использованы при вычислениях, потому что иррациональные действительные числа требуют для своей записи бесконечного числа знаков. В криптографии используются только целые числа, так как операции с ними математически точны.

Конгруэнтные генераторы

Из простейших процедур, имитирующих случайные числа, наиболее употребляем так называемый конгруэнтный способ, приписываемый Д.Х. Лемеру. Множество чисел, сгенерированных при помощи криптографического генератора псевдослучайных чисел, широко используется для шифрования информации и сигналов при их передаче. Наиболее доступными и эффективными являются так называемые конгруэнтные генераторы ПСП. Последовательность описывается следующим рекуррентным соотношением:

, ,

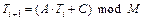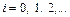где Т ₀ – исходная величина, т.е. число, порождающее последовательность; М – обычно 2 ^b – длина слова в битах 2⁸, 2¹⁶ и т.д.; А, C – подбираются таким образом, чтобы период порождающей последовательности был максимальным. Доказано, что он максимален, когда C – нечетное, (А mod 4)=1.

Например, если выбрать С =3, А =5, M =256, t₀ =1, то получим следующую последовательность чисел:

t₁ =8; t₂ =43;… t₂₅₄ =71; t₂₅₅ =102; t₂₅₆ =1; t₂₅₇ =8; t₂₅₈ =43….

Видно, что период полученной последовательности равен 2⁸. В реальной ситуации величина M обычно составляет 2¹⁶, 2³², 2⁶⁴.

Генератор Парка-Миллера

,

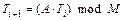где 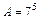, M =2³¹-1.

Иногда используют квадратичные и кубические конгруэнтные генераторы, которые обладают большей стойкостью к взлому.

Квадратичный конгруэнтный генератор имеет вид

.

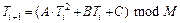Кубический конгруэнтный генератор задается как

.

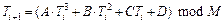Для увеличения размера периода повторения конгруэнтных генераторов часто используют их объединение. При этом криптографическая безопасность не уменьшается, но такие генераторы обладают лучшими характеристиками в некоторых статистических тестах.

Реальные генераторы случайных последовательностей

Для любого генератора важным вопросом является его проверка. Тесты на случайность можно найти в Internet. Доказано, что все из описанных выше генераторов можно воспроизвести. Это только вопрос времени.

В мощных криптосистемах военного применения используются действительно случайные генераторы чисел, основанные на настоящем физическом источнике случайной информации, которую невозможно предсказать. Примеры таких источников включают радиоактивное излучение, шумящие полупроводниковые приборы, дробовой шум в электронной лампе, младшие биты оцифрованного звука, интервалы между нажатиями клавиш. Получаемые на практике устройства, использующие данные источники, оказываются очень громоздкими и сложными, хотя известны случаи удачных применений их в генерации ключей, например, в российском криптографическом устройстве КРИПТОН.

Когда нет настоящего физического источника шума, приходится пользоваться псевдослучайными числами. На компьютерах общего назначения желательно получить некий шум окружения – скажем от величины задержек в устройствах, цифры статистики текущего использования ресурсов, сетевой статистики, прерываний от клавиатуры или чего-то иного. Задачей является получить данные, непредсказуемые для внешнего наблюдателя. К основным способам получения реальных случайных последовательностей относятся следующие:

1. Использование специальных таблиц RAND.

2. Использование случайного шума.

3. Использование таймера компьютера.

4. Измерение скрытого состояния клавиатуры.

5. Аппаратно-временные характеристики компьютера:

- положение мыши на экране монитора;

- текущий номер сектора и дорожки дисковода или винчестера;

- номер текущей строки развертки монитора;

- времена поступления сетевых пакетов.

В программах шифрования вместо физических процессов для генерации гаммы применяют программы для ЭВМ, которые хотя и называются генераторами случайных чисел, но на самом деле они выдают детерминированные числовые ряды и только кажутся случайными по своим свойствам. Можно сформулировать следующие требования к криптографически стойкому генератору псевдослучайной последовательности (ПСП) или гаммы:

1. Период гаммы должен быть достаточно большим для шифрования сообщений различной длины.

2. Гамма должна быть трудно предсказуемой. Это значит, что если известны тип генератора и кусок гаммы, то невозможно предсказать следующий за этим куском бит (или число) гаммы с вероятностью выше заданной P. Если криптоаналитику станет известна какая-то часть гаммы, он все же не сможет определить биты, предшествующие ей или следующие за ней.

3. Генерирование гаммы не должно быть связано с большими техническими и организационными трудностями.

Самая важная характеристика генератора псевдослучайных чисел − информационная длина периода, после которого числа либо начнут просто повторяться, либо их можно будет предсказывать. Эта длина фактически определяет возможное число ключей системы и зависит от алгоритма получения псевдослучайных чисел. Требуемую длину периода определяет степень секретности данных. Чем длиннее ключ, тем труднее его подобрать.

Криптографические генераторы псевдослучайных чисел обычно используют большой пул, содержащий случайную информацию. Биты генерируются путем выборки из пула с возможным прогоном через криптографическую однонаправленную функцию, чтобы сделать содержимое пула невидимым для внешнего наблюдателя. Когда требуется новая порция бит, пул перемешивается путем шифровки со случайным ключом (его можно взять из неиспользованной части пула) так, чтобы каждый бит пула зависел от каждого другого бита. Новый шум окружения должен добавляться к пулу перед перемешиванием, чтобы сделать предсказание новых значений пула еще более сложным.