Шифр Цезаря как впрочем, и другие шифры замены и перестановки расшифровать довольно легко.
Считаем, что известны вероятности букв pi, i=1, 2.., n, в языке сообщения (n – число букв в алфавите). Определяем частоты букв fi в зашифрованном сообщении. Если сообщение довольно длинное, то будет выполняться fi≈ pi. Затем необходимо делать перебор по сдвигам (разным ключам). Когда сдвиг не угадан, то общее различие между pi и fi(N) равное будет велико. Минимум величины 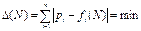 говорит о том, что сдвиг N угадан верно, где N – это ключ к расшифровке кода Цезаря.
говорит о том, что сдвиг N угадан верно, где N – это ключ к расшифровке кода Цезаря.
15. Простейшие шифры замены и перестановки: шифр Атбаш, квадрат Полибия, код Виженера, шифрование с помощью скитала, магические квадраты и книжный шифр.
Шифр Атбаш:
Шифр Атбаш - Шифр простой замены, использованный для еврейского алфавита и получивший оттуда свое название. Шифрование происходит заменой первой буквы алфавита на последнюю, второй на предпоследнюю.
Для английского алфавита:
Исходный алфавит: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Алфавит замены: Z Y X W V U T S R Q P O N M L K J I H G F E D C B A
Для русского алфавита:
Исходный алфавит: А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я
Алфавит замены: Я Ю Э Ъ Ы Ь Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Ё Е Д Г В Б А
Шифр Полибия:
Древней Греции (П в. до н. э.) был известен шифр, называемый "квадрат Полибия". Это устройство представляло собой квадрат 5x5, столбцы и строки которого нумеровали цифрами от 1 до 5. В каждую клетку этого квадрата записывалась одна буква. (В греческом варианте одна клетка оставалась пустой, в латинском - в одну клетку помещали две буквы i и j.) В результате каждой букве отвечала пара чисел и шифрованное сообщение превращалось в последовательность пар чисел.

Например: 13 34 22 24 44 34 15 42 22 34 43 45 32
Это сообщение записано при использовании латинского варианта "квадрата Полибия ", в котором буквы расположены в алфавитном порядке.
Шифр Виженера:
Этот шифр удобнее всего представлять себе как шифр Цезаря с переменной величиной сдвига. Чтобы знать, на сколько сдвигать очередную букву открытого текста, заранее договариваются о способе запоминания сдвигов. Сам Виженер предлагал запоминать ключевое слово, величину сдвига. Существует алгоритм шифрования по таблице Виженера:
1-я строка - фраза для шифрования;
2-я строка - номера букв фразы для шифрования в русском алфавите;
3-я строка- ключевое слово с длиной равной длине фразы;
4-я строка - номера букв ключевого слова в алфавите;
5-я строка - сумма номеров 2-й и 4-й строк в соответствующих столбцах;
6-я строка - результат «вычитания полного оборота» 33 буквы;
7-я строка - зашифрованная фраза.
Дешифровка осуществляется по обратному алгоритму, с учётом того, что 5-я строка - разность 2-й и 4-й строки. Если число 2-й строки меньше числа 4-й строки, считаем так: 33 + число 2-й строки – число 4-й строки.
А-1 Б-2 В-3 Г-4 Д-5 Е-6 Ё-7 Ж-8 З-9 И-10 Й-11 К-12 Л-13 М-14 Н-15 О-16 П-17 Р- 18 С-19 Т- 20 У-21 Ф-22 Х-23 Ц- 24 Ч-25 Ш- 26 Щ-27 Ъ- 28 Ы-29 Ь-30 Э-31 Ю-32 Я-33

Шифр перестановки "скитала"
Известно, что в V веке до нашей эры правители Спарты, наиболее воинственного из греческих государств, имели хорошо отработанную систему секретной военной связи и шифровали свои послания с помощью скитала, первого простейшего криптографического устройства, реализующего метод простой перестановки. Шифрование выполнялось следующим образом. На стержень цилиндрической формы, который назывался скитала, наматывали спиралью (виток к витку) полоску пергамента и писали на ней вдоль стержня несколько строк текста сообщения (рис.1.). Затем снимали со стержня полоску пергамента с написанным текстом. Буквы на этой полоске оказывались расположенными хаотично. Такой же результат можно получить, если буквы сообщения писать по кольцу не подряд, а через определенное число позиций до тех пор, пока не будет исчерпан весь текст.
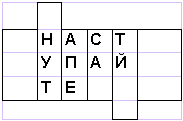
Сообщение НАСТУПАЙТЕ при размещении его по окружности стержня по три буквы дает шифртекст НУТАПЕСА_ТЙ
Для расшифрования такого шифртекста нужно не только знать правило шифрования, но и обладать ключом в виде стержня определенного диаметра. Зная только вид шифра, но не имея ключа, расшифровать сообщение было непросто. Шифр скитала многократно совершенствовался в последующие времена.
КНИЖНЫЙ шифр
Заметным вкладом Энея в криптографию является предложенный им так называемый книжный шифр, описанный в сочинении «Об обороне укреплённых мест». Эней предложил прокалывать малозаметные дырки в книге или в другом документе над буквами секретного сообщения. Интересно отметить, что в первой мировой войне германские шпионы использовали аналогичный шифр, заменив дырки на точки, наносимые симпатическими чернилами на буквы газетного текста.
Книжный шифр в современном его виде имеет несколько иной вид. Суть этого шифра состоит в замене букв на номер строки и номер этой буквы в строке в заранее оговоренной странице некоторой книги. Ключом такого шифра является книга и используемая страница в ней. Этот шифр оказался «долгожителем» и применялся даже во времена второй мировой войны.
МАГИЧЕСКИЕ квадраты
Во времена средневековья европейская криптография приобрела сомнительную славу, отголоски которой слышатся и в наши дни. Криптографию стали отождествлять с черной магией, с некоторой формой оккультизма, астрологией, алхимией, еврейской каббалой. К шифрованию информации призывались мистические силы. Так, например, рекомендовалось использовать «магические квадраты».
В квадрат размером 4 на 4 (размеры могли быть и другими) вписывались числа от 1 до 16. Его магия состояла в том, что сумма чисел по строкам, столбцам и полным диагоналям равнялась одному и тому же числу - 34.
Впервые эти квадраты появились в Китае, где им и была приписана некоторая «магическая сила». Приведем пример:
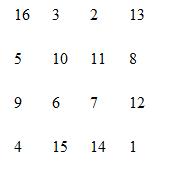
Шифрование по магическому квадрату производилось следующим образом. Например, требуется зашифровать фразу: «Приезжаю сегодня». Буквы этой фразы вписываются последовательно в квадрат согласно записанным в них числам, а в пустые клетки ставятся произвольные буквы.

После этого шифрованный текст записывается в строку: УИРДЗЕГЮСЖАОЕЯНП
При расшифровывании текст вписывается в квадрат и открытый текст читается в последовательности чисел «магического квадрата». Данный шифр -обычный шифр перестановки, но считалось, что особую стойкость ему придает волшебство «магического квадрата».
16. Основные характеристики систем с секретным ключом DES, FEAL, IDEA, ГОСТ 28147-89, RC5.
| Название шифра | Исторические сведения | Основные характеристики |
| DES –Data Encryption Standard (стандарт шиф- рования данных) | Разработан в середине 70-х годов сотрудником корпорации IBM Х. Фейстелем | Данный шифр основан на сети Фейштеля. Шифруется блок из 64 бит, используется 64-битовый ключ (требуется только 56 бит), 16 проходов. Может работать в 4 режимах. |
| FEAL –Fast Data Encipherment Algorithm (быстрый алгоритм шифрования) | Предложен 1987 г. как альтернатива DES | Ориентирован на 8 разрядный процессор; длина ключа 64 бита |
| IDEA –International Data Encryption Algorithm (междуна- родный алгоритм шифрования) | Предложен в 1991 г. | 64- битные блоки открытого текста последовательно шифруются на 128 битном ключе, 8 проходов |
| ГОСТ 28147-89 | Отечественный алго- ритм блочного шифро- вания. Разработан в середине 80-х годов в СССР. | Предусматривает 3 режима шифрования: простой замены, гаммирования и гаммирования с обратной связью; размер блока 64 бита, длина ключа 256 бит. |






