На этапе синтаксического анализа нужно установить, имеет ли цепочка лексем структуру, заданную синтаксисом языка, и зафиксировать эту структуру. Следовательно, снова надо решать задачу разбора: дана цепочка лексем, и надо определить, выводима ли она в грамматике, определяющей синтаксис языка. Однако структура таких конструкций как выражение, описание, оператор и т.п., более сложная, чем структура идентификаторов и чисел. Поэтому для описания синтаксиса языков программирования нужны более мощные грамматики, чем регулярные. Обычно для этого используют укорачивающие контекстно-свободные грамматики (УКС-грамматики), правила которых имеют вид A ® a, где A Î VN,
a Î (VT È VN) *. Грамматики этого класса, с одной стороны, позволяют достаточно полно описать синтаксическую структуру реальных языков программирования; с другой стороны, для разных подклассов УКС-грамматик существуют достаточно эффективные алгоритмы разбора.
С теоретической точки зрения существует алгоритм, который по любой данной КС-грамматике и данной цепочке выясняет, принадлежит ли цепочка языку, порождаемому этой грамматикой. Но время работы такого алгоритма (синтаксического анализа с возвратами) экспоненциально зависит от длины цепочки, что с практической точки зрения совершенно неприемлемо.
Существуют табличные методы анализа ([3]), применимые ко всему классу КС-грамматик и требующие для разбора цепочек длины n времени cn3 (алгоритм Кока-Янгера-Касами) либо cn2 (алгоритм Эрли). Их разумно применять только в том случае, если для интересующего нас языка не существует грамматики, по которой можно построить анализатор с линейной временной зависимостью.
Алгоритмы анализа, расходующие на обработку входной цепочки линейное время, применимы только к некоторым подклассам КС-грамматик. Рассмотрим один из таких методов.
Метод рекурсивного спуска
Пример: пусть дана грамматика G =({a,b,c, ^}, {S,A,B}, P, S), где
P: S ® AB^
A ® a | cA
B ® bA
и надо определить, принадлежит ли цепочка caba языку L(G).
Построим вывод этой цепочки:
S ® AB^ ® cAB^ ® caB^ ® cabA^ ® caba^
Следовательно, цепочка принадлежит языку L(G).
Последовательность применений правил вывода эквивалентна построению дерева разбора методом "сверху вниз":


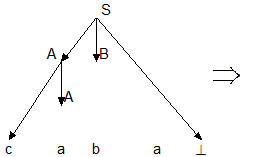


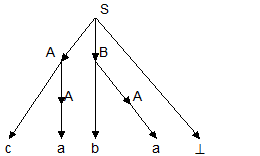
Метод рекурсивного спуска (РС-метод) реализует этот способ практически "в лоб": для каждого нетерминала грамматики создается своя процедура, носящая его имя; ее задача - начиная с указанного места исходной цепочки найти подцепочку, которая выводится из этого нетерминала. Если такую подцепочку считать не удается, то процедура завершает свою работу вызовом процедуры обработки ошибки, которая выдает сообщение о том, что цепочка не принадлежит языку, и останавливает разбор. Если подцепочку удалось найти, то работа процедуры считается нормально завершенной и осуществляется возврат в точку вызова. Тело каждой такой процедуры пишется непосредственно по правилам вывода соответствующего нетерминала: для правой части каждого правила осуществляется поиск подцепочки, выводимой из этой правой части. При этом терминалы распознаются самой процедурой, а нетерминалы соответствуют вызовам процедур, носящих их имена.
Пример: совокупность процедур рекурсивного спуска для грамматики
G = ({a,b,c,^}, {S,A,B}, P, S), где
P: S ® AB^
A ® a | cA
B ® bA
будет такой:
#include <stdio.h>
int c;
FILE *fp;/*указатель на файл, в котором находится анализируе-мая цепочка */
void A();
void B();
void ERROR(); /* функция обработки ошибок */
void S() {A(); B();
if (c!= '^') ERROR();
}
void A() {if (c=='a') c = fgetc(fp);
else if (c == 'c') {c = fgetc(fp); A();}
else ERROR();
}
void B() {if (c == 'b') {c = fgetc(fp); A();}
else ERROR();
}
void ERROR() {printf("ERROR!!!\n"); exit(1);}
main() {fp = fopen("data","r");
c = fgetc(fp);
S();
printf("SUCCESS!!!\n"); exit(0);
}






