Замечание: если при описании грамматики указаны только правила вывода Р, то будем считать, что большие латинские буквы обозначают нетерминальные символы, S - цель грамматики, все остальные символы - терминальные.
1) Язык типа 0: L(G) = {a2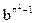 
| n >= 1}
G: S ® aaCFD
F ® AFB | AB
AB ® bBA
Ab ® bA
AD ® D
Cb ® bC
CB ® C
bCD ® e
2) Язык типа 1: L(G) = { an bn cn, n >= 1}
G: S ® aSBC | abC
CB ® BC
bB ® bb
bC ® bc
cC ® cc
3) Язык типа 2: L(G) = {(ac)n (cb)n | n > 0}
G: S ® aQb | accb
Q ® cSc
4) Язык типа 3: L(G) = {w ^ | w Î {a,b}+, где нет двух рядом стоящих а}
G: S ® A^ | B^
A ® a | Ba
B ® b | Bb | Ab
Разбор цепочек
Цепочка принадлежит языку, порождаемому грамматикой, только в том случае, если существует ее вывод из цели этой грамматики. Процесс построения такого вывода (а, следовательно, и определения принадлежности цепочки языку) называется разбором.
С практической точки зрения наибольший интерес представляет разбор по контекстно-свободным (КС и УКС) грамматикам. Их порождающей мощности достаточно для описания большей части синтаксической структуры языков программирования, для различных подклассов КС-грамматик имеются хорошо разработанные практически приемлемые способы решения задачи разбора.
Рассмотрим основные понятия и определения, связанные с разбором по КС-грамматике.
Определение: вывод цепочки b Î (VT)* из S Î VN в КС-грамматике
G = (VT, VN, P, S), называется левым (левосторонним), если в этом выводе каждая очередная сентенциальная форма получается из предыдущей заменой самого левого нетерминала.
Определение: вывод цепочки b Î (VT)* из S Î VN в КС-грамматике
G = (VT, VN, P, S), называется правым (правосторонним), если в этом выводе каждая очередная сентенциальная форма получается из предыдущей заменой самого правого нетерминала.
В грамматике для одной и той же цепочки может быть несколько выводов, эквивалентных в том смысле, что в них в одних и тех же местах применяются одни и те же правила вывода, но в различном порядке.
Например, для цепочки a+b+a в грамматике
G = ({a,b,+}, {S,T}, {S ® T | T+S; T ® a | b}, S)
можно построить выводы:
(1) S®T+S®T+T+S®T+T+T®a+T+T®a+b+T®a+b+a
(2) S®T+S®a+S®a+T+S®a+b+S®a+b+T®a+b+a
(3) S®T+S®T+T+S®T+T+T®T+T+a®T+b+a®a+b+a
Здесь (2) - левосторонний вывод, (3) - правосторонний, а (1) не является ни левосторонним, ни правосторонним, но все эти выводы являются эквивалентными в указанном выше смысле.
Для КС-грамматик можно ввести удобное графическое представление вывода, называемое деревом вывода, причем для всех эквивалентных выводов деревья вывода совпадают.
Определение: дерево называется деревом вывода ( или деревом разбора) в КС-грамматике G = {VT, VN, P, S), если выполнены следующие условия:
(1) каждая вершина дерева помечена символом из множества (VN È VT È e), при этом корень дерева помечен символом S; листья - символами из (VT È e);
(2) если вершина дерева помечена символом A Î VN, а ее непосредственные потомки - символами a1, a2,..., an, где каждое ai Î (VT È VN), то A ® a1a2...an - правило вывода в этой грамматике;
(3) если вершина дерева помечена символом A Î VN, а ее единственный непосредственный потомок помечен символом e, то A ® e - правило вывода в этой грамматике.
Пример дерева вывода для цепочки a+b+a в грамматике G:
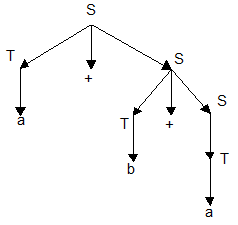
Определение: КС-грамматика G называется неоднозначной, если существует хотя бы одна цепочка a Î L(G), для которой может быть построено два или более различных деревьев вывода.
Это утверждение эквивалентно тому, что цепочка a имеет два или более разных левосторонних (или правосторонних) выводов.
Определение: в противном случае грамматика называется однозначной.
Определение: язык, порождаемый грамматикой, называется неоднозначным, если он не может быть порожден никакой однозначной грамматикой.
Пример неоднозначной грамматики:
G = ({if, then, else, a, b}, {S}, P, S),
где P = {S ® if b then S else S | if b then S | a}.
В этой грамматике для цепочки if b then if b then a else a можно построить два различных дерева вывода.
Однако это не означает, что язык L(G) обязательно неоднозначный. Определенная нами неоднозначность - это свойство грамматики, а не языка, т.е. для некоторых неоднозначных грамматик существуют эквивалентные им однозначные грамматики.
Если грамматика используется для определения языка программирования, то она должна быть однозначной.
В приведенном выше примере разные деревья вывода предполагают соответствие else разным then. Если договориться, что else должно соответствовать ближайшему к нему then, и подправить грамматику G, то неоднозначность будет устранена:
S ® if b then S | if b then S’ else S | a
S’ ® if b then S’ else S’ | a
Проблема, порождает ли данная КС-грамматика однозначный язык (т.е. существует ли эквивалентная ей однозначная грамматика), является алгоритмически неразрешимой.
Однако можно указать некоторые виды правил вывода, которые приводят к неоднозначности:
(1) A ® AA | a
(2) A ® AaA | b
(3) A ® aA | Ab | g
(4) A ® aA | aAbA | g
Пример неоднозначного КС-языка:
L = {ai bj ck | i = j или j = k}.
Интуитивно это объясняется тем, что цепочки с i = j должны порождаться группой правил вывода, отличных от правил, порождающих цепочки с j = k. Но тогда, по крайней мере, некоторые из цепочек с i = j = k будут порождаться обеими группами правил и, следовательно, будут иметь по два разных дерева вывода. Доказательство того, что КС-язык L неоднозначный, приведен в [3, стр. 235-236].
Одна из грамматик, порождающих L, такова:
S ® AB | DC
A ® aA | e
B ® bBc | e
C ® cC | e
D ® aDb | e
Очевидно, что она неоднозначна.
Дерево вывода можно строить нисходящим либо восходящим способом.
При нисходящем разборе дерево вывода формируется от корня к листьям; на каждом шаге для вершины, помеченной нетерминальным символом, пытаются найти такое правило вывода, чтобы имеющиеся в нем терминальные символы “проектировались” на символы исходной цепочки.
Метод восходящего разбора заключается в том, что исходную цепочку пытаются “свернуть” к начальному символу S; на каждом шаге ищут подцепочку, которая совпадает с правой частью какого-либо правила вывода; если такая подцепочка находится, то она заменяется нетерминалом из левой части этого правила.
Если грамматика однозначная, то при любом способе построения будет получено одно и то же дерево разбора.
Преобразования грамматик
В некоторых случаях КС-грамматика может содержать недостижимые и бесплодные символы, которые не участвуют в порождении цепочек языка и поэтому могут быть удалены из грамматики.
Определение: символ x Î (VT È VN) называется недостижимым в грамматике G = (VT, VN, P, S), если он не появляется ни в одной сентенциальной форме этой грамматики.
Алгоритм удаления недостижимых символов:
Вход: КС-грамматика G = (VT, VN, P, S)
Выход: КС-грамматика G’ = (VT’, VN’, P’, S), не содержащая недостижимых символов, для которой L(G) = L(G’).
Метод:
1. V0 = {S}; i = 1.
2. Vi = {x | x Î (VT È VN), в P есть A®axb и AÎVi-1, a,bÎ(VTÈVN)*} È Vi-1.
3. Если Vi ¹ Vi-1, то i = i + 1 и переходим к шагу 2, иначе VN’ = Vi Ç VN;
VT’ = Vi Ç VT; P’ состоит из правил множества P, содержащих только символы из Vi; G’ = (VT’, VN’, P’, S).
Определение: символ A Î VN называется бесплодным в грамматике
G = (VT, VN, P, S), если множество { a Î VT* | A Þ a} пусто.
Алгоритм удаления бесплодных символов:
Вход: КС-грамматика G = (VT, VN, P, S).
Выход: КС-грамматика G’ = (VT, VN’, P’, S), не содержащая бесплодных символов, для которой L(G) = L(G’).
Метод:
Рекурсивно строим множества N0, N1,...
1. N0 = Æ, i = 1.
2. Ni = {A | (A ® a) Î P и a Î (Ni-1 È VT)*} È Ni-1.
3. Если Ni ¹ Ni-1, то i = i + 1 и переходим к шагу 2, иначе VN’ = Ni; P’ состоит из правил множества P, содержащих только символы из VN’ È VT; G’ = (VT, VN’, P’, S).
Определение: КС-грамматика G называется приведенной, если в ней нет недостижимых и бесплодных символов.
Алгоритм приведения грамматики:
(1) обнаруживаются и удаляются все бесплодные нетерминалы.
(2) обнаруживаются и удаляются все недостижимые символы.
Удаление символов сопровождается удалением правил вывода, содержащих эти символы.
Замечание: е сли в этом алгоритме переставить шаги (1) и (2), то не всегда результатом будет приведенная грамматика.
Для описания синтаксиса языков программирования стараются использовать однозначные приведенные КС-грамматики.
Задачи.
1. Дана грамматика. Построить вывод заданной цепочки.
a) S ® T | T+S | T-S b) S ® aSBC | abC
T ® F | F*T CB ® BC
F ® a | b bB ® bb
Цепочка a-b*a+b bC ® bc
cC ® cc
Цепочка aaabbbccc
2. Построить все сентенциальные формы для грамматики с правилами:
S ® A+B | B+A
A ® a
B ® b
3. К какому типу по Хомскому относится данная грамматика? Какой язык она порождает? Каков тип языка?
a) S ® APA b) S ® aQb | e
P ® + | - Q ® cSc
A ® a | b
c) S ® 1B d) S ® A | SA | SB
B ® B0 | 1 A ® a
B ® b
4. Построить грамматику, порождающую язык:
a) L = { an bm | n, m >= 1}
b) L = { acbcgc | a, b, g - любые цепочки из a и b}
c) L = { a1 a2... an an... a2 a1 | ai = 0 или 1, n >= 1}
d) L = { an bm | n ¹ m; n, m >= 0}
e) L = { цепочки из 0 и 1 с неравным числом 0 и 1}
f) L = { aa | a Î {a,b}+}
g) L = { w | w Î {0,1}+ и содержит равное количество 0 и 1, причем любая подцепочка, взятая с левого конца, содержит единиц не меньше, чем нулей}.
h) L = { (a2m bm)n | m >= 1, n >= 0}
i) L = {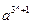 
^ | n >= 1}
j) L = {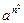 
| n >= 1}
k) L = {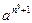 
| n >= 1}
5. К какому типу по Хомскому относится данная грамматика? Какой язык она порождает? Каков тип языка?
a) S ® a | Ba b) S ® Ab
B ® Bb | b A ® Aa | ba
c) S ® 0A1 | 01 d) S ® AB
0A ® 00A1 AB ® BA
A ® 01 A ® a
B ® b
*e) S ® A | B *f) S ® 0A | 1S
A ® aAb | 0 A ® 0A | 1B
B ® aBbb | 1 B ® 0B | 1B | ^
*g) S ® 0S | S0 | D *h) S ® 0A | 1S | e
D ® DD | 1A | e A ® 1A | 0B
A ® 0B | e B ® 0S | 1B
B ® 0A | 0
*i) S ® SS | A *j) S ® AB^
A ® a | bb A ® a | cA
B ® bA
*k) S ® aBA | e *l) S ® Ab | c
B ® bSA A ® Ba
AA ® c B ® cS
6. Эквивалентны ли грамматики с правилами:
а) S ® AB и S ® AS | SB | AB
A ® a | Aa A ® a
B ® b | Bb B ® b
b) S ® aSL | aL и S ® aSBc | abc
L ® Kc cB ® Bc
cK ® Kc bB ® bb
K ® b
7. Построить КС-грамматику, эквивалентную грамматике с правилами:
а) S ® aAb b) S ® AB | ABS
aA ® aaAb AB ® BA
A ® e BA ® AB
A ® a
B ® b
8. Построить регулярную грамматику, эквивалентную грамматике с правилами:
а) S ® A | AS b) S ® A. A
A ® a | bb A ® B | BA
B ® 0 | 1
9. Доказать, что грамматика с правилами:
S ® aSBC | abC
CB ® BC
bB ® bb
bC ® bc
cC ® cc
порождает язык L = {an bn cn | n >= 1}. Для этого показать, что в данной грамматике
1) выводится любая цепочка вида an bn cn (n >= 1) и
2) не выводятся никакие другие цепочки.
10. Дана грамматика с правилами:
a) S ® S0 | S1 | D0 | D1 b) S ® if B then S | B = E
D ® H. E ® B | B + E
H ® 0 | 1 | H0 | H1 B ® a | b
Построить восходящим и нисходящим методами дерево вывода для цепочки:
a) 10.1001 b) if a then b = a+b+b
11. Определить тип грамматики. Описать язык, порождаемый этой грамматикой. Написать для этого языка КС-грамматику.
S ® P^
P ® 1P1 | 0P0 | T
T ® 021 | 120R
R1 ® 0R
R0 ® 1
R^® 1^
12. Построить регулярную грамматику, порождающую цепочки в алфавите
{a, b}, в которых символ a не встречается два раза подряд.
13. Написать КС-грамматику для языка L, построить дерево вывода и левосторонний вывод для цепочки aabbbcccc.
L = {a2n bm c2k | m=n+k, m>1}.
14. Построить грамматику, порождающую сбалансированные относительно круглых скобок цепочки в алфавите { a, (,), ^ }. Сбалансированную цепочку a определим рекуррентно: цепочка a сбалансирована, если
a) a не содержит скобок,
b) a = (a1) или a= a1 a2, где a1 и a2 сбалансированы.
15. Написать КС-грамматику, порождающую язык L, и вывод для цепочки aacbbbcaa в этой грамматике.
L = {an cbm can | n, m>0}.
16. Написать КС-грамматику, порождающую язык L, и вывод для цепочки 110000111 в этой грамматике.
L = {1n 0m 1p | n+p>m; n, p, m>0}.
17. Дана грамматика G. Определить ее тип; язык, порождаемый этой грамматикой; тип языка.
G: S ® 0A1
0A ® 00A1
A ® e
18. Дан язык L = {13n+2 0n | n>=0}. Определить его тип, написать грамматику, порождающую L. Построить левосторонний и правосторонний выводы, дерево разбора для цепочки 1111111100.
19. Привести пример грамматики, все правила которой имеют вид
A ® Bt, либо A ® tB, либо A ® t, для которой не существует эквивалентной регулярной грамматики.
20. Написать общие алгоритмы построения по данным КС-грамматикам G1 и G2, порождающим языки L1 и L2, КС-грамматики для
a) L1ÈL2
b) L1 * L2
c) L1*
Замечание: L =L1 * L2 - это конкатенация языков L1 и L2, т.е.L = { ab | a Î L1, b Î L2}; L = L1* - это итерация языка L1, т.е. объединение {e} È L1 È L1*L1 È L1*L1*L1 È...
21. Написать КС-грамматику для L={wi 2 wi+1R | i Î N, wi=(i)2 - двоичное представление числа i, wR - обращение цепочки w}. Написать КС-грамматику для языка L* (см. задачу 20).
22. Показать, что грамматика
E ® E+E | E*E | (E) | i
неоднозначна. Как описать этот же язык с помощью однозначной грамматики?
23. Показать, что наличие в КС-грамматике правил вида
a) A ® AA | a
b) A ® AaA | b
c) A ® aA | Ab | g
где a, b, g Î (VTÈVN)*, A Î VN, делает ее неоднозначной. Можно ли преобразовать эти правила таким образом, чтобы полученная эквивалентная грамматика была однозначной?
*24. Показать, что грамматика G неоднозначна. Какой язык она порождает? Является ли этот язык однозначным?
G: S ® aAc | aB
B ® bc
A ® b
25. Дана КС-грамматика G={VT, VN, P, S}. Предложить алгоритм построения множества
X={A Î VN | A Þ e}.
26. Для произвольной КС-грамматики G предложить алгоритм, определяющий, пуст ли язык L(G).
27. Написать приведенную грамматику, эквивалентную данной.
a) S ® aABS | bCACd b) S ® aAB | E
A ® bAB | cSA | cCC A ® dDA | e
B ® bAB | cSB B ® bE | f
C ® cS | c C ® cAB | dSD | a
D ® eA
E ® fA | g
28. Язык называется распознаваемым, если существует алгоритм, который за конечное число шагов позволяет получить ответ о принадлежности любой цепочки языку. Если число шагов зависит от длины цепочки и может быть оценено до выполнения алгоритма, язык называется легко распознаваемым. Доказать, что язык, порождаемый неукорачивающей грамматикой, легко распознаваем.
29. Доказать, что любой конечный язык, в который не входит пустая цепочка, является регулярным языком.
30. Доказать, что нециклическая КС-грамматика порождает конечный язык.
Замечание: Нетерминальный символ A Î VN - циклический, если в грамматике существует вывод A Þ x1Ax2. КС-грамматика называется циклической, если в ней имеется хотя бы один циклический символ.
31. Показать, что условие цикличности грамматики (см. задачу 30) не является достаточным условием бесконечности порождаемого ею языка.
32. Доказать, что язык, порождаемый циклической приведенной КС-грамматикой, содержащей хотя бы один эффективный циклический символ, бесконечен.
Замечание: Циклический символ называется эффективным, если A Þ aAb, где |aAb| > 1; иначе циклический символ называется фиктивным.
