ТММ
Курсовое проектирование
Учебное пособие
Волгоград
2016 г.
УДК 531.8
Рецензенты:
Доктор технических наук, профессор кафедры «Теплоэнергетика и теплотехника» Волжского филиала национального исследовательского университета «МЭИ» Грига А.Д.,
Канд. тех. наук, доцент кафедры Общетехнические дисциплины» Волжского института строительства и технологий (филиала) ФГБОУ ВПО «Волгоградский государственный архитектурно-строительный университет» Горин Н.И.
Издается по решению редакционно-издательского совета
Волгоградского государственного технического университета
Саразов, А.В.: ТММ Курсовое проектирование. [ Электронный ресурс ]: Учебное пособие /А.В. Саразов, К.В. Худяков //Сборник «Учебные пособия». Серия «Технические дисциплины». Электрон. текстовые дан. (1файл: 4,7 MB) – Волгоград: ВПИ (филиал) ВолгГТУ,2016.–систем.требования: Windows 95 и выше; ПК с процессором 486+; CD-ROM.
Содержит указания к выполнению курсового проекта (курсовой работы) по теории механизмов и машин. Задания также могут быть использованы студентами для самоподготовки. Предназначены для студентов, обучающихся по всем направлениям бакалавриата».
Ил. 19, табл. 1, библиограф. 5 назв.
| Ó Волгоградский государственный технический университет, 2016 Ó Волжский политехнический институт, 2016 |
Введение
Задание на курсовое проектирование выдается студентам на первом практическом занятии по ТММ и включает в себя номер задания и номер варианта, ряд числовых значений различных параметров механизмов и буквенное обозначение диаграммы аналога ускорения выходного звена кулачкового механизма.
Объем и содержание курсового проекта (работы) устанавливается рабочей программой по направлению бакалавриата.
Курсовой проект (работа) состоит из пояснительной записки и графической части (3(4) листа формата А1).
Основные задачи, решаемые при проектировании: кинематическое исследование механизма, кинетостатический расчет механизма, синтез одноступенчатой эвольвентной зубчатой передачи, синтез планетарной передачи, синтез кулачкового механизма.
Выполняемый курсовой проект (работа) проверяется преподавателем кафедры, после чего проводится его защита. На защите студент должен показать знания теории и общих методов анализа и синтеза механизмов.
Общие положения
Целью работы является закрепление теоретических знаний, полученных при прослушивании курса лекций и приобретение практических навыков при расчете механизмов.
В курсовом проекте (работе) решаются задачи структурного, кинематического и кинетостатического анализа рычажных механизмов, а также синтеза прямозубой цилиндрической эвольвентной зубчатой передачи, планетарного редуктора и кулачкового механизма.
Состав курсового проекта (работы)
Курсовой проект (работа) состоит из расчетно-пояснительной записки и графической части, содержащей схемы и диаграммы.
Состав графической части следующий:
1. Кинематический и кинетостатический анализ рычажного механизма, включающий в себя план положений механизма (2-12 позиций), планы скоростей для 2-12 положений механизма, планы ускорений для двух положений механизма, планы сил для двух положений механизма, рычаг Жуковского для 1-2 положений механизма.
2. Синтез привода, включающий в себя синтез прямозубой цилиндрической эвольвентной зубчатой передачи, построение диаграмм относительного скольжения, синтез и кинематическое исследование планетарного редуктора.
3. Синтез кулачкового механизма, включающий в себя графическое интегрирование функции аналога ускорения, определение минимального радиуса кулачка, построение профиля кулачка методом обратного вращения.
Оформление курсового проекта (работы)
Графические построения выполняются на листах формата А1 карандашом или черной тушью. Лист может быть создан на компьютере и отпечатан с применением печатающих и графических устройств вывода согласно требованиям ЕСКД.
Форматы листов определяются размерами внешней рамки, выполненной тонкой линией.
На чертежах обязательно сохранять все вспомогательные построения, делать соответствующие надписи и проставлять принятые масштабы.
Начертание линий их толщина, чертежные шрифты на чертежах выбираются согласно ГОСТ 2.303, 2.304.
Основные надписи располагаются в правом нижнем углу чертежа и должны соответствовать ГОСТ 2.104.
Размеры на чертежах не должны повторяться. Размеры указывают в миллиметрах без обозначения единиц измерения. Угловые размеры указываются в градусах, минутах и секундах с указанием единиц измерения.
Планы положений механизмов, планы скоростей, ускорений механизмов, планы сил, диаграммы сил, размерность которых отлична от линейных размеров, могут выполняться в произвольных, но удобных для построения и чтения масштабах (в пояснительной записке и на чертеже указывается масштабный коэффициент μ).
Изображение должно иметь наименование, при необходимости – масштаб, в случае повторения – номер позиции. Наименования помещаются над или под изображением. Под наименованием размещается масштаб и номер позиции. Номер позиции выполняется арабскими цифрами в круге основной линии чертежа диаметром 12 мм.
Диаграммы выполняются в соответствии с ГОСТ 2.319-81. Оси координат, ограничивающие диаграммы, выполняются сплошными основными линиями, линии сетки и делительные штрихи – сплошной тонкой линией. На диаграммах без сетки оси координат ограничиваются стрелками.
Если началом отсчета шкал является нуль, то его следует указывать один раз у точки пересечения шкал.
Обозначения параметров на диаграммах выполняются в виде символов в конце шкалы после последнего числа. Единица измерения помещается под символом в виде дроби, например, 
. Допускаются и другие обозначения параметров в рамках ГОСТ 2.319-81.
Оформление расчетно-пояснительной записки
Расчетно-пояснительная записка должна быть выполнена на бумаге формата А4 и должна содержать:
1) титульный лист и лист задания;
2) содержание;
3) основную часть в соответствие с заданием (расчеты и пояснения к ним);
4) список использованных источников;
5) приложения (при необходимости).
Текстовая часть проекта оформляется в соответствии с «Общими требованиями к текстовым документам» по ГОСТ 2.107.
Текст следует оформлять, выдерживая следующие поля: слева – 30 мм, справа – 10 мм, сверху – 15 мм, снизу – 20 мм. Допускается оформление текста пояснительной записки с рамкой (ГОСТ 2.105).
Абзацы в тексте начинают отступом, равным 15-17 мм.
Текст может быть написан аккуратно от руки чернилами одного цвета (высота букв не менее 2,5 мм), либо отпечатан на компьютере с соблюдением требований: шрифт Times New Roman, кегль 14, интервал полуторный.
Листы записки должны иметь сквозную нумерацию. Номер страниц проставляется арабскими цифрами в правом нижнем углу без точки. На титульном листе и задании номера страниц не проставляются.
Текстовая часть записки должна ограничиваться краткими комментариями к расчету с записью расчетной формулы. Терминология должна соответствовать общепринятой в научно-технической литературе.
Названия разделов в записке соответствуют названиям разделов задания. Каждый раздел начинается с новой страницы, имеет заголовок. Подразделы (например, «Кинетостатический расчет механизма»,
«Определение сил инерции») должны быть отделены от остального текста, быть визуально заметными. Переносы слов в заголовках не допускаются. Названия подраздела, пункта и т.д. не допускается помещать на разных страницах.
Между концом предыдущего раздела и заголовком следующего рекомендуется соблюдать расстояние 2 интервала.
В тексте не допускается употреблять математические знаки без цифр, например >, = и т.д. Разрывать предложение текста рисунками или таблицами не допускается.
Ссылка на литературные источники оформляется прямоугольными скобками, внутри которых указывается номер источника в прилагаемом списке использованной литературы и (при необходимости) номера страниц. Например: [1], [1, c.25-26].
Все уравнения и формулы записываются в общем виде, а затем в них подставляются необходимые числовые значения, при этом указывается размерность полученной величины в системе СИ. В формулах в качестве символов следует применять обозначения установленные стандартами (м, а не м-р, Н, а не Н-н и т.д.). пояснения к формуле принято начинать с новой строки со слова «где».
Уравнения и формулы следует выделять из текста в отдельную строку. Формулы нумеруют арабскими цифрами в пределах раздела. Например, формула в разделе №2 оформляется так:
Масштаб плана скоростей вычисляется по формуле (2.1).
(2.1)
где μv- масштаб плана скоростей, 
,
vА – скорость точки А, м/с,
ра – длина соответствующего отрезка на плане скоростей, мм.
Формулы, следующие одна за другой и не разделенные текстом, разделяют запятой.
При оформлении таблиц в левом верхнем углу пишется слово «Таблица», ставится ее номер и затем название через тире и с прописной буквы. Например: Таблица 2 – Параметры зубчатого зацепления. Таблица помещаются по тексту после ссылки на нее и на отдельную страницу не выносится. Высота строк таблицы должна быть не менее 8мм.
Таблица 2.3 – Значения ускорений точек механизма.
| Положение механизма | Размер ность | Ускорения точек | |||||||||
| WА | 
| 
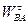
| WВ, WS3 | Wc | 
| 
| Wf, WS5 | WS2 | WS4 | ||
| мм | 17,5 | ||||||||||
| м/с2 | 1,26 | ||||||||||
| мм | 6,6 |
Иллюстрации (рисунки, схемы, диаграммы) располагают непосредственно после текста, в котором они упоминаются, или на следующей странице.
Иллюстрации следует нумеровать арабскими цифрами сквозной нумерацией в пределах раздела. Слово «Рисунок» и наименование помещают после пояснительных данных. Пример: Рисунок 1.2 – Кинематическая схема механизма. При ссылках на иллюстрации следует писать «в соответствии с рисунком 1.2».
Задания
Номер и вариант задания выдает преподаватель. В каждом задании предлагается 5 различных вариантов значений параметров и несколько параметров, имеющих индивидуальные значения для каждого студента. Примеры заданий к курсовой работе (проекту) представлены в приложении А (допускается использование заданий из других источников).
Структурный анализ механизма
Структурный анализ механизма является первым этапом работы. Он состоит в определении числа подвижных звеньев механизма, числа кинематических пар, класса каждой пары, числа степеней подвижности и включает также разложение механизма на группы. Группы необходимо отделять так, чтобы движение оставшейся части механизма не претерпело в результате этого никаких изменений. Важно также усвоить правильную последовательность отделения групп. В дальнейшем все построения производятся в обратном порядке, то есть в порядке присоединения групп к исходному двухзвенному механизму.
Алгоритм проведения структурного анализа
1. Начертить кинематическую схему механизма.
2. Обозначить все подвижные звенья механизма.
3. Заглавными буквами латинского алфавита обозначить все кинематические пары и класс кинематической пары.
4. Определить степень подвижности механизма.
5. Удалить лишние степени свободы (если они есть).
6. Удалить пассивные связи (если они есть).
7. Заменить высшие кинематические пары на низшие.
8. Отсоединить от механизма группу Ассура второго класса (два звена) так чтобы, оставшийся механизм продолжал работать, а степень его подвижности (W) не менялась (оставалась прежней).
9. Если нельзя отсоединить группу Ассура второго класса, то отсоединить группу Ассура третьего класса (четыре звена) так чтобы, оставшийся механизм продолжал работать, a (W) не менялась.
10. Если нельзя отсоединить группу Ассура третьего класса, то отсоединить группу Ассура четвертого класса, так чтобы оставшийся механизм продолжал работать, a (W) механизма не менялась.
11. Класс механизма определяется по наивысшему классу группы Ассура, входящей в состав механизма.
Пример проведения структурного анализа
Произведем структурный анализ механизма, изображенного на рис. 1.
|
Рис. 1. Кинематическая схема механизма
Степень подвижности механизма: W = 3n - 2p5 - p4 = 3∙5 - 2∙7 = l.
Разложим механизм на структурные группы, для чего составим структурную схему механизма (Рис. 2). Поступательные кинематические пары заменяем вращательными. Нулевое звено (стойку) изображаем неподвижной прямой 0. Ведущее звено 1 изображаем отрезком с двумя шарнирами (цифра 1 в записи кинематических пар встречается дважды). Аналогично звено 2 изображаем отрезком 2 с двумя шарнирами на концах.
Рис. 2. Структурная схема механизма
Третье звено изображаем треугольником (цифра 3 в записи кинематических пар встречается трижды); звенья 4 и 5 изображаем отрезками с двумя кинематическими парами. Звенья 1,3,5 замыкаются на нулевое звено.
Отсоединяем сначала двухповодковую группу Ассура, состоящую из звеньев 4,5. При этом оставшийся механизм продолжает работать, а степень подвижности W не меняется. Затем отсоединяем двухповодковую группу Ассура, состоящую из звеньев 2 и 3. Оставшиеся два звена 0 и 1 образуют ведущий механизм.
|
|
|
Рис. 3. Группы Ассура
Таким образом, изображаемый механизм, обладающий одной степенью подвижности, можем рассматривать как образованный путем последовательного присоединения к стойке О и ведущему звену 1 двух групп, состоящих из звеньев 2, 3 и 4, 5. По классификации И.И. Артоболевского он относится к механизмам 2 класса, третьего семейства.
Формула строения механизма: I(0,1)→II(2,3)→III(4,5).
Кинематический анализ механизма
Кинематическое исследование проводится графически – построением совмещенных планов положений механизма, соответствующих 2 - 12 равноотстоящим положениям ведущего звена, начиная с крайнего положения, соответствующего началу рабочего хода выходного звена.
Если дана диаграмма силы полезного сопротивления в зависимости от перемещения выходного звена, вычертить диаграмму рядом с траекторией движения выходного звена.
Для 2 - 12 положений механизма строятся планы скоростей, с помощью которых определяют скорости известных точек звеньев, угловые скорости звеньев.
Для 2 положений механизма строятся планы, с помощью которых определяют линейные ускорения всех точек механизма, в том числе центров масс звеньев, а также угловые ускорения звеньев.
Кинематическое исследование механизма занимает площадь до одного листа формата А1.
Построение положений звеньев механизма.
План положений механизма является первым построением, выполняемым на листе. От точности данного построения будет зависеть и точность планов скоростей и ускорений. На плане положений последовательные положения механизма строятся не отдельно друг от друга, а совместно.
Выбрав масштаб длин μe, находим все необходимые размеры в мм. Длину любого отрезка на чертеже получим, поделив истинное значение его на масштабный коэффициент, т.е.
; 
.
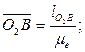
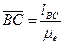Имея значения отрезков 
, 
, 
вычерчиваем кинематическую схему механизма.
Согласно заданию ведущее звено механизма — кривошип О1А —вращается равномерно, следовательно, равным участкам пути точки А соответствуют равныепромежутки времени. Поэтому, разделив траекторию движения точки А (окружность радиуса О1А) соответственно на 8, 12, 24 и 48 равных частей, получим положения кривошипа в различные моменты времени. При этом за нулевое положение кривошипа принимается такое, при котором скорость ведомого (рабочего) звена механизма равна нулю, а ползун занимает наиболее удаленное от точки О1 положение. Для механизма это случается тогда, когда кривошип О2В и шатун ВС располагаются на одной прямой (рис.4). Соответствующее положение точки С0 определим, сделав из точки О2 засечку на траектории движения ползуна С радиусом О2С = О2В + ВС. Точка пересечения отрезка О2С с траекторией движения кривошипа О2В (окружность радиуса О2В) дает положение точки В0, а точка пересечения прямой О2С с траекторией движения точки А кривошипа О1А дает положение точки А0, а следовательно, нулевое положение кривошипа О1А. Разбивка траектории точки А должна начаться от положения О1А0.
Получив все положения кривошипа, находим положения точки В и ползуна С, и соединяя получившиеся точки прямыми линиями, получим совмещенные планы положения механизма. При этом два исследуемые положения выделяются более жирными линиями для последующего более подробного анализа.
Рис. 4. Планы положений механизма
План положений механизма позволяет получить размеченную траекторию любой точки механизма и затем построить диаграммы перемещений, скоростей и ускорений этой точки. Кроме того, план положений позволяет решить и ряд других вопросов: отсутствие препятствий движению звеньев со стороны каких-либо неподвижных частей; форма закрытого корпуса механизма; соотношение между временем движения возвратно-поступательного (или возвратно-вращательного) движения звена в одном и другом направлениях и т.д.
Определение скоростей точек и угловых скоростей звеньев
Кинематическое исследование механизма осуществляется для каждой структурной группы в порядке их присоединения.
Скорости точек механизма определяется графоаналитическим способом для каждого плана положения в зависимости от угла поворота кривошипа. Метод состоит в графическом решении векторных уравнений.
Сначала определяются скорости точек ведущего механизма. Если ведущее звено совершает вращательное движение, то скорость точки А (Рис. 5, 6, 7) по величине определяется из выражения
где 
-угловая скорость вращения кривошипа.
Из полюса Р плана скоростей в направлении вращения кривошипа перпендикулярно к OA откладываем вектор скорости точки A, где pa - отрезок в мм (обычно длину отрезка выбирают в пределах 60-100 мм), затем определяется масштаб плана скоростей 
.
Построение остальных точек плана зависит от схемы механизма, в частности от присоединённых двухповодковых групп, которые можно разделить на три типа: с вращательными кинематическими парами, с вращательно-поступательными парами и с поступательньно-вращательными парами.
Сначала рассматривается двухповодковая группа, присоединённая к начальному звену, т.е. группа, которой принадлежит шарнир А. Затем определяются точки второй двухповодковой группы, присоединённой к первой и так далее до последней группы.
Построение плана скоростей рассмотрим на примере шарнирного четырёхзвенника О1АВО2 (Рис. 5).
Рис. 5. План скоростей и план ускорений для шарнирного четырехзвенника
К кривошипу 1 присоединена группа звеньев 2-3, состоящая из шатуна 2, совершающего плоское движение, и коромысла 3, совершающего вращательное движение. План скоростей точки А уже построен. Вектор 
и направлен в сторону вращения ω1.
Для определения скорости точки В составляем векторное уравнение
в котором векторы делятся на два вида: известные по величине и направлению, и известные только по направлению.
Строим треугольник скоростей точки В, для чего из полюса плана скоростей Р проводим перпендикуляр к звену 3, а из точки а – перпендикуляр к звену 2. Точка пересечения перпендикуляров определяет положение точки b на плане скоростей, а вектор 
изображает вектор скорости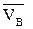 
точки В. Скорости других точек шатуна и коромысла определятся из подобия треугольников или пропорций отрезков. Так положение точки С на плане скоростей определяется пресечением перпендикуляров проведённых из точки а к звену АС, а из точки b к звену ВС. Вектор 
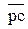изображает вектор скорости Vс точки С. Положения точек S2, S3 и d определяются отрезкам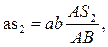и 
и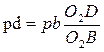 
; откладываем эти отрезки на плане скоростей. Соединяем полученные точки S2, S3 и d с полюсом плана скоростей Р. Векторы 
, 
, 
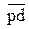изображают вектора скоростей точек S2, S3 и d.
Значения линейных скоростей всех точек определяются выражениями: 
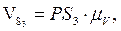
Значения окружных скоростей точек определяются аналогично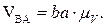 
Величины угловых скоростей шатуна и коромысла определяются на основе построения плана скоростей
Для определения направления угловой скорости ω2 следует мысленно перенести вектор 
в точку В (первая по записи точка) плана положения механизма и посмотреть куда поворачивается звено относительно точки А (вторая по записи точка). В эту сторону будет направлена угловая скорость.
Аналогично определяется направление угловой скорости ω3.
План скоростей двухповодковой группы с вращательно-поступательными парами.
Построение плана скоростей рассмотрим на примере кривошипно-ползунного механизма (рис.6.)
Рис. 6. План скоростей и план ускорений для кривошипно-ползунного механизма
К кривошипу 1 присоединена группа звеньев 2-3, состоящая из шатуна 2, совершающего плоское движение, и ползуна 3, совершающего поступательное движение.
Из произвольной точки Р (полюса плана скоростей) в направлении вращения кривошипа перпендикулярно к OA откладываем вектор скорости точки А 
, где 
; 
; 
Определяем масштаб плана скоростей 
Составляем векторное уравнение скорости точки В
Строим треугольник скоростей точки В в соответствии с уравнением, для чего из точки а проводим прямую, перпендикулярную к звену 2 (линия вектора ), а через полюс Р проводим прямую параллельную ОВ (линия вектора 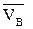). Пересечение этих двух прямых определяет точку b, которая является концом вектора , изображающего на плане вектор скорости точки В. Положение других точек шатуна на плане скоростей определяется из подобия треугольников, либо из пропорции отрезков, так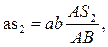
Откладываем отрезок 
на плане, соединяем точку S2 с полюсом Р плана и получаем вектор . Значения линейных скоростей точек определяются произведением длин отрезков на масштаб плана скоростей.
Угловая скорость вращения шатуна по величине будет равна 
Направление ω2 определяется переносом вектора в точку В плана положения механизма и вращением звена относительно точки А под действием этого вектора.
План скоростей двухповодковой группы с поступательно-вращательными кинематическими парами.
Под этой группой понимают такое соединение звеньев при котором поступательная кинематическая пара находится в плоскопараллельном движении. Построение плана скоростей рассмотрим на примере кулисного механизма (Рис. 7).
Рис. 7. План скоростей и план ускорений для механизма с двухповодковой группой
К кривошипу 1 присоединена группа звеньев 2-3, состоящая из камня кулисы 2 и кулисы 3, совершающей вращательное движение вокруг точки O2.
Из полюса Р плана скоростей в направлении вращения кривошипа, перпендикулярно к O1A откладываем вектор абсолютной скорости точки А1 кривошипа 
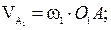
Определяем масштаб плана скоростей 
Скорости точки А2 камня кулисы равна скорости точки A1 
и равна геометрической сумме скоростей точки в переносном движении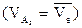 
и скорости точки в относительном движении 
, 
, т.е.
Строим треугольник скоростей в соответствии с уравнением, для чего из начала вектора 
проводим перпендикуляр к кулисе 02А, а из конца вектора 
проводим линию, параллельную кулисе 02А до взаимного пересечения. Получаем точку а3. Векторы 
и 
являются векторами переносной 
и относительной 
скоростей точки А соответственно.
Величины этих скоростей будут равны 
Величина угловой скорости кулисы 
Направление ω3 определяется направлением вращения кулисы под действием вектора .
Определение ускорений точек и угловых ускорений
звеньев механизма
Определение линейных ускорений точек звеньев происходит в той же последовательности, что и определение скоростей. Ускорения точек определяются путём построения планов ускорений для каждого положения механизма.
Сначала определяются ускорения точек ведущего звена. Если ведущее звено совершает равномерное вращательное движение, то ускорение наиболее удалённой точки А равно нормальному ускорению 
и направлено по радиусу вращения к центру вращения (Рис. 5 - 7).
Из полюса плана ускорений - π откладываем вектор 
параллельно звену O1A в направлении от точки А и точке 01 в соответствии со схемой механизма. Длина этого вектора изображает на плане ускорений вектор ускорения точки A 
и выбирается произвольно, исходя из удобства размещения на чертеже. (Обычно ра = 60 – 120 мм )
Определяем масштаб плана ускорений μW
Ускорения остальных точек плана ускорений механизма зависит от присоединённых групп Ассура.
План ускорений двухповодковой группы с вращательными
парами
Построение плана ускорений рассмотрим на примере шарнирного четырехзвенника О1АВО2 (Рис. 5).
Ускорение точки В складывается из ускорения точки А и относительного ускорения точки В при вращении звена 2 вокруг точки А. С другой стороны точка В принадлежит звену 3 и движется по окружности вокруг точки О2. Таким образом, имеем систему двух векторных уравнений
Нормальные составляющие ускорений равны по величине.
и 
,
где аb и pb - отрезки, взятые из плана скоростей.
Нормальное ускорение 
направлено вдоль звена АВ от точки В к точке А, а нормальное ускорение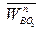 
- вдоль звена ВО2 от точки В к точке О2.
Тангенциальные составляющие ускорений 
и 
по величине неизвестны, известны по направлению: 
; 
Решаем совместно систему уравнений графически. Из конца вектора 
(точки а) откладываем вектор 
|| АВ, направленный от точки В к точке А, величина которого равна 
, а из полюса π откладываем вектор 
|| ВО2 направленный от точки В к точке О2, величина которого равна 
. Затем из точки n проводим линию действия вектора 
, которая 
АВ, а из точки n1 — линию действия вектора 
, которая ВO2. На пересечении линий получаем точку b. Соединив точку b с полюсом π, получаем вектор ускорения точки В 
Ускорение других точек шатуна и коромысла определяются из подобия треугольников или пропорций отрезков.
Для определения положения точки С на плане ускорений строим треугольник abc, подобный треугольнику ABC на плане положений механизма, для чего отрезок ab на плане ускорений поворачиваем вокруг точки а на угол α, а вокруг точки b на угол β, сохраняя правило обхода контура до пересечения повернутых отрезков.
Положение точек S2, S3 и d определяются отрезкам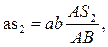и 
и 
Откладываем эти отрезки на плане ускорений. Соединим полученньи точки S2, S3, d с полюсом плана ускорений π. Векторы 
, 
, 
изображают векторы ускорений точек S2, S3, d.
Значения ускорений всех точек определяются выражениями:
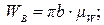
Значения угловых ускорений шатуна 2 и коромысла 3 определяются следующими выражениями:
Направление углового ускорения ε2определяется направлением вращения звена 2 вокруг точки А под действием вектора касательного ускорения , приложенного в точке В плана положения механизма. Для данного положения ускорение ε2направлено по часовой стрелке.
Аналогично определяется направление ускорения ε3.
План ускорений двухповодковой группы с вращательно-поступательными кинематическими парами.
Построение плана ускорений рассмотрим на примере кривошипно-ползунного механизма (рис. 6).
Из полюса плана ускорений πоткладываем вектор 
ускорения точки А кривошипа.
Ускорение точки В находим по уравнению
Нормальное ускорение точки В вокруг точки А 
величине равна 
. Из конца вектора ускорения точки А 
откладываем вектор || ВА, направленный от точки В к точке А, величина которого равна . Затем из точки n проводим линию действия касательного ускорения 
, которая АВ, а из полюса плана ускорений πпроводим линию || ускорению 
(горизонтальная линия). На пересечении линий получаем точку b. Получаем вектор ускорений точки В - 
.
Ускорения любой точки шатуна определяются аналогично определению скоростей точек на плане скоростей.
Угловое ускорение шатуна ε2 определяется аналогично тому, как это было сделано ранее.
План ускорений двухповодковой группы с поступательно-вращательными кинематическими парами.
Построение плана ускорений рассмотрим на примере кулисного механизма (Рис. 7).
Первой точкой ускорение которой следует определить, является точка А1 ведущего звена (кривошипа OA). Из полюса плана ускорений πоткладываем вектор параллельно звену AO1 в направлении от точки А к точке О.
Следующая точка А2, принадлежащая камню кулисы. Ускорения точек А1 и А2 будут равны (шарнирное соединение), т.е. 
.
Точка А2 совершает сложное движение её ускорение складывается из ускорений точки A3 (переносное движение точки) и ускорения точки А2 при движении звена 2 по звену 3 (относительное движение точки), т.е.
Поскольку траекторией движения точки А3 является окружность, то переносное ускорение точки A3 состоит из двух частей 
, где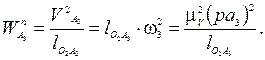 
Поскольку звено 3 совершает вращение вокруг неподвижной оси, то относительное ускорение точки состоит из двух частей: 
, где 
- кориолисово ускорение точки. Величина ускорения Кориолиса равна
Для определения направления ускорения Кориолиса следует вектор относительной скорости 
повернуть на 90° в сторону вращения, обусловленного угловой скоростью ω3. Итак:
Строим план ускорений точки А2 согласно уравнению.
Из полюса плана скоростей π откладываем вектор 
|| О2А,направленный от точки А к точке О2, размер которого определяется 
, а из точки n проводим линию действия вектора 
, которая O2А. Далее из конца вектора (точки a12) откладываем вектор 
O2А, направленный к точке a (вектор 
должен подходить к точке a), размер которого определяется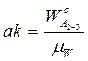 
. Затем из точки К проводим линию действия вектора 
, которая || O2А. На пересечении линий получаем точку a3 Соединяя точки πи a3, получим ускорение точки 
. Значения ускорений определяется из выражений:
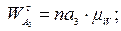
Величина углового ускорения ε3 определяется по выражению:
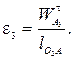
Направление ε3 определяется направлением вращения звена 3 вокруг точки О2 под действием вектора ускорения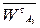 
приложенного в точке А плана положения механизма. Для данного положения механизма ускорение ε3 направлено против часовой стрелки.
Графическое определение длин отрезков нормального и Кориолисова ускорений на плане ускорений
Нормальное и кориолисово ускорения можно определить путём вычисления по формулам. Однако для построения плана ускорений важно знать не сами ускорения, а длину выражающих их отрезков. Например, длина вектора, выражающего в масштабе 
нормальное ускорение точки А равна
или 
где (ab) - отрезок на плане скоростей; AB - отрезок на плане положений.
Величина 
повторяется при вычислении каждого нового ускорения и её можно вычислить заранее. Целесообразно выбирать так, чтобы указанная величина была равна некоторому круглому числу или, ещё лучше, единице.
Тогда 
и вычисления значительно упрощаются.
Более наглядны и практически безошибочны графические способы вычисления, в качестве примера на рис. 8 построен отрезок n.
Рис. 8. Вычисление ускорений
Берётся произвольный угол, на одной её стороне откладывается отрезок АВ, снятый из плана положений, и на обеих сторонах отрезок ab = ab, снятый с плана скоростей. Точка В и b соединяются прямой линией, а через b проводится прямая, || Вb до пересечения с прямой ab в точке X. Отрезок ах и является искомым.
Аналогично построение отрезка С 
; 
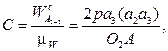выражающего Кориолисово ускорение 
масштабе 
. Отрезки ра3 и аa3 снимаются с плана скоростей, отрезок O2A с плана положений. Построения нормальных и кориолисовых ускорений выполняются на листе и снабжаются соответствующими заголовками.
Кинетостатический расчет механизма
Расчет производится для 2 положений механизма в следующей последовательности:
Задачей силового анализа является:
1) Определение сил инерции звеньев.
2) Определение давлений в кинематических парах.
3) Определение уравновешивающей силы на ведущем звене.
Известными являются геометрические размеры звеньев, закон движения ведущего звена, внешние силы и моменты.
Силовой анализ механизмов имеет важное значение, так как по найденным давлениям в кинематических парах подбираются подшипники, производится расчет на прочность и жесткость звеньев механизмов, элементов кинематических пар и т.д.
Силовые исследования выполняются в следующем порядке:
1) Структурным анализом определяют номер семейства кинематической цепи, степень подвижности, класс и порядок механизма.
2) Кинематическим анализом определяют скорости и ускорения точек и звеньев механизма.
3) Собственно силовой анализ начинают с последней группы Ассура. При силовом исследовании механизма используется принцип Даламбера, согласно которому звено или группа звеньев механизма рассматриваются в состоянии равновесия, если к внешним силам и моментам, действующим на них, добавить силы и моменты сил инерции. Уравнения равновесия в этом случае называют уравнениями кинетостатики.
Решая задачу силового анализа механизма в курсовом проекте (работе), рекомендуется, сделав следующие допущения: силы трения в кинематических парах малы, ими следует пренебречь; ведущее звено исполнительного механизма (кривошип) вращается с постоянной угловой скоростью (ω1= const); звенья механизма имеют плоскость симметрии параллельную плоскости их движения, определить:
1) силы полезного сопротивления для всех положений;
2) давление во всех кинематических парах в указанных положениях механизма;
3) уравновешивающий момент в указанных положениях механизма двумя методами (методом плана сил и методом Н. Е. Жуковского: полученные результаты сравнить (расхождение вычисленных уравновешивающих моментов должно быть в пределах 5 %).
Внешние нагрузки, действующие на звенья механизма
Основными силами являются движущие силы, совершающие положительную работу и силы полезного сопротивления, возникающие в процессе выполнения работы и совершающие отрицательную работу.
К движущим силам Fд относятся: сила давления рабочей смеси на
поршень цилиндра двигателя; момент, развиваемый электродвигателем на выходном валу насоса или компрессора и т.д.
Силами полезного сопротивления Fc является: силы сопротивления резанию в токарном или строгальном станках, силы сопротивления сжимаемого воздуха и т.д.
Внешние силы могут быть постоянными по величине, такие как, например силы тяжести, силы сопротивления резанию металла при постоянном сечении снимаемой стружки. Они могут зависеть от положения звена, на которое они действуют (силы давления газов, действующие на поршень двигателя внутреннего сгорания или компрессора); от скорости (момент электродвигателя); от времени и т.д.
Значения внешних воздействующих должны быть заданы соответствующими механическими характеристиками. Механические характеристики представляют собой аналитические или графические зависимости внешних сил (моментов) от кинематических параметров (обобщенной координаты, обобщенной скорости, времени). Имея характеристику механизма, можно определить силы механизируемого процесса, приложенные к выходному звену или силы движущие, приложенные к входному звену. Например, если представлена индикаторная диаграмма изменения давления газов 
в цилиндре двигателя (компрессора), то силу можно рассчитать по формуле: 
где - давление приходящееся на 1 мм2 площади поршня.
Силы тяжести звеньев механизма прикладываются в центрах тяжести звеньев и по величине равны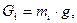 
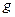где - ускорение свободного падения; 
- масса 
- го звена.
Силы инерции звеньев плоских механизмов
Звено совершает поступательное движение (рис. 9). Силы инерции точек звена заменяются главным вектором сил инерции 
, приложенным в центре тяжести звена, равным по величине произведению массы звена 
на ускорение центра масс звена 
и направленным в сторону, противоположную ускорению центра масс 
. Равнодействующая сил инерции звена 
совпадает в этом случае с главным вектором сил инерции 
;
Звено совершает вращение вокруг оси с постоянной угловой
скоростью 
. Главный вектор сил инерции 
приложен
в центре масс 
звена, направлен по радиусу кривизны ОА от центра кривизны О и равен 
. Равнодействующая сил инерции равна главному вектору сил инерции, т.е 
;
Звено вращается с переменой угловой скоростью 
. В этом случае силы инерции точек звена проводятся к главному вектору сил инерции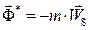 
, приложенному в центре масс и к главному моменту сил инерции 
, направленному против углового ускорения звена 
, где 
- момент инерции звена относительно оси, проходящей через центр масс. Главный вектор сил инерции 
и главный момент сил инерции 
могут быть заменены равнодействующей сил инерции 
, векторно-равной главному вектору (
) и приложенной в центре качания звена 
, 
положение которого определяется зависимостью
Звено совершает плоскопараллельное движение. Силы
инерции точек звена проводятся к главному вектору сил инерции,
приложенному в центре масс 
звена и к главному моменту сил инерции относительно центра масс: 
; 
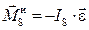. Главный вектор сил инерции и главный момент сил инерции могут быть заменены равнодействующей сил инерции 
, векторно равной главному вектору ()и приложенной в центре инерции, положение которого видно из
построения (рис). Линия 
параллельна ускорению полюса 
. Линия КТ параллельна относительному ускорению 
.
Рис. 9. Определение сил инерции звеньев
Последовательность силового анализа механизмов по способу планов сил
Силовой расчет целесообразно проводить в следующей последовательности:
Вычертить кинематическую схему механизма в выбранном масштабе и в заданном или указанном преподавателем расчетном положении (желательно в пределах рабочего хода).
Определить все внешние силы, приложенные к звеньям механизма: изобразить характеристику рассматриваемой машины (индикаторная диаграмма, график зависимости силы полезного сопротивления от положения ползуна), определить силу полезного сопротивления для всех положений (в пояснительной записке составить таблицу этих сил)
Построить или перенести с первого листа курсового проекта план ускорений для рассматриваемого положения механизма, указать на схеме направления угловых ускорений и вычислить силы и моменты сил инерции.
Приложить в виде стрелок без масштаба в соответствующие точки кинематической схемы силу полезного сопротивления, силы тяжести, силы и момента сил инерции. К входному звену (кривошипу) приложить уравновешивающий момент при приводе механизма от электродвигателя, направив его по движению звена, или уравновешивающую силу 
, чтобы был обеспечен заданный закон движения ведущего звена.
Произвести расчленение кинематической схемы механизма на группы Ассура и группу начальных звеньев, изобразить каждую группу отдельно и нанести все приложенные силы и моменты, заменив действие «отброшенных» звеньев реакциями, приложенными к элементам кинематических пар.
Произвести силовой расчет каждой группы Ассура в отдельности, так как группа Ассура являются статически определимой системой. Расчет следует начинать с группы Ассура присоединенной к механизму при его образовании в последнюю очередь; затем перейти к следующей группе и так до тех пор, пока не будет произведен силовой расчет всех групп, образовавших ведомую часть механизма.
В заключение производится силовой расчет ведущего звена, в результате которого определяется идеальный уравновешивающий момент и также нормальная реакция со стороны стойки на кривошип.
Определение уравновешивающего момента (силы) методом Н. Е. Жуковского
При решении задач (например, определения мощности двигателя) часто бывает необходимо определить только уравновешивающий момент (силу). Для решения этой задачи удобно применять метод Н. Е. Жуковского (рис. 10)
Н.Е. Жуковский сформулировал теорему, которая гласит: если силу, приложенную к какой либо точке звена плоского механизма, перенести параллельно себе в одноименную точку повернутого на 90° плана скоростей, то момент этой силы относительно полюса плана скоростей будет пропорционален ее мощности.
Согласно общего уравнения динамики системы (принципа Даламбера-Лагранжа) чтобы механическая система, на которую изложены совершенные, голономные, удерживающие связи, находилась в равновесии необходимо и достаточно, чтобы сумма элементарных работ (мощностей) всех заданных сил и сил инерции на возможном перемещение системы равнялась нулю, т.е 
или 
. Согласно теореме Н.Е. Жуковского общее уравнение динамики системы равносильно уравнению моментов всех активных сил и сил инерции относительно полюса повернутого на 90° плана скоростей, т.е
