S: выберите правильный вариант ответа
Q: вид нагружения бруса, когда в поперечном сечении бруса одновременно действуют несколько внутренних усилий, называется:
+: сложным сопротивлением
-: плоским изгибом
-: поперечным изгибом
-: продольным изгибом
S: выберите правильный вариант ответа
Q: для определения напряжений при сложном сопротивлении используется:
+: принцип суперпозиции
-: принцип Сен-Венана
-: гипотеза Бернулли
-: закон Гука
S: выберите правильный вариант ответа
Q: пространственный изгиб вызывается:
+: моментами, расположенными в разных плоскостях, проходящих через ось балки
-: моментами, расположенными в разных плоскостях, не проходящих через ось балки
-: моментами, расположенными в плоскости, не проходящей через ось балки
-: моментами, расположенными в плоскости, проходящей через ось балки
S: выберите правильный вариант ответа
Q: вид пространственного изгиба, когда нагрузки лежат в одной плоскости, не совпадающей ни с одной из главных плоскостей, называется:
+: косым изгибом
-: плоским изгибом
-: изгибом с растяжением
-: изгибом с кручением
S: выберите правильный вариант ответа
Q: при пространственном изгибе нормальные напряжения определяют по формуле:
+: 
-: 
-: 
-: 
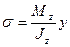
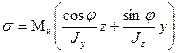
1. Закон Гука справедлив до напряжения соответствующему
+ пределу пропорциональности материала
2. Коэффициент Пуассона для известных конструкционных материалов находится в пределах
+ 0 ≤ v ≤ 0,5
3. Какая связь существует между упругими константами – модулем сдвига G, модулем Юнга Е и коэффициентом Пауссона?
+ G=E/2(1+v)
4. Способность твёрдого тела сопротивляться внешним нагрузкам, не разрушаясь, называется...
+ прочностью
5. Предел отношения равнодействующей ∆P внутренних сил, действующих на площадку ∆A, к велечине площади ∆A, когда последняя стремился к нулю 
, определяет величину вектора...
+ полного напряжения
6. Изменение размеров или формы тела под действием внешних сил называется
+ деформированным состоянием
7. Материал называется изотропным, если...
+ свойства образца, выделенного из материала, не зависят от его угловой ориентации
8. Пластичностью называется свойство материала...
+ сохранять некоторую часть деформации после снятия нагрузки
9. Способность тела под нагрузкой сохранять заданную форму равновесия называется...
+ устойчивостью
10. К характеристике главных площадок нельзя отнести...
+ число таких площадок в каждой точке нагруженного объекта может быть неограниченным
11. Действие главных напряжений показано на рисунке
 |
12. Касательные напряжения не...
+ вызывают изменение объёма нагруженного твёрдого тела
13. В случае объёмного напряженного состояния максимальные касательные напряжения в точках нагруженного объекта можно определить как τ...
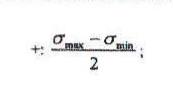
14. Главная относительная линейная деформация это...
+ деформации в направлении главного напряжения
15. Обобщенный закон Гука это...
+ 
16. Условия прочности по энергетической теории прочности представляется неравенством
+ 
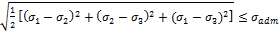
17. Из классификации напряженного состояния нужно исключить понятие
+ общего напряженного состояния
18. К характеристике внутренних напряжений не относится утверждение о том, что они...
+ не связаны с деформациями
19. Расчёт на прочность и жёсткость в условиях сложного сопротивления производится на основе...
+ принципа суперпозиции
20. Первая теория прочности основана на ограничении...
+ наибольших растягивающих нормальных напряжений
21. В нагруженном твёрдом теле напряжения в общем случае не зависят от...
+ материала
22. Внутренние силовые факторы в поперечных сечениях бруса не зависят от
+ размера и формы сечения
23. Сколько внутренних силовых факторов возникает в поперечных сечениях стержня в общем случае нагружения
+ шесть
24. Какая гипотеза положена в основу теории растяжения (сжатия) прямолинейных стержней?
+ гипотеза плоских сечений
25. Изотропным материалом не является...
+ древесина
26. Внутренние силовые факторы в сечениях нагруженных объектов определяются с помощью...
+ интеграла Мора
27. В основном объектами изучения сопротивления материалов являются...
+ элементы в виде бруса контрукции из них
28. К основным гипотезам сопротивления материалов не следует относить...
+ гипотезу сплошности
29. Для определения внутренних силовых факторов в поперечных сечениях нагруженного бруса нужно..
+ составить уравнения равновесия для одной из частей
30. Чистый сдвиг является частным случаем...
+ плоского напряженного состояния
31. При расчёте на прочность ограничиваются максимальные значения...
+ напряжений
32. Все известные теории прочности приводят к одинаковым результатам
+ при растяжении стержней
33. Вектор полного напряжения на данной площадке p раскладывают на составляющие (на нормаль к площадке и на плоскость этой площадки). Эти составляющие называют...
+ нормальными и касательными напряжениями
34. Изменение положения в пространстве одного тела (или частицы тела) относительно другого тела в различные фиксированные моменты времени называется...
+ перемещением
35. В сечении 1-1 имеют место внутренние силовые факторы...
+ 
36. Чугун и сталь – материалы...
+ изотропные
37. В поперечном сечении стержня, изображенного на рисунке, действуют внутренние силовые факторы...
+ N и 
38. В сечении 1-1 имеют место внутренние силовые факторы...
1 M
2a 2a
+ 
39. Упругостью называется свойства материала...
+ восстанавливать свою форму и размеры после снятия нагрузки
40. В модели формы при расчётах прочностной надежности вводят упрощение в геометрию элементов конструкций, приводят их к схеме...
+ стержня, пластинки, оболочки и массива
41. Предел отношения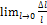 
называется...
+ относительной линейной деформацией в точке
42. Компонент вектора полного напряжения p, действующего в некоторой точке сечения тела, определяемый проекцией вектора p на плоскость сечения называется...
+ касательным напряжением 
43. Какие основные задачи решаются в курсе сопртивления материалов...
+ задачи прочности, устойчивости, жесткости
44. Жёсткость называется...
+ способность тела воспринимать воздействие внешних сил без существенного изменения геометрических размеров
45. Главные напряжения связаны между собой следующим соотношением...
+ 
46. Относительное изменение объёма для изотропного тела вычисляется по формуле...
+ 
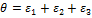
47. Удельная потенциальная энергия упругой деформации вычисляется по формуле...
+ 
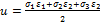
48. Первая классическая теория прочности имеет вид...
+ 
49. Вторая классическая теория прочности имеет вид...
+ 
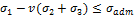
50. Третья теория прочности имеет вид...
+ 
51. Четвёртая теория прочности имеет вид..
+
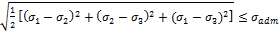
52. Коэффициент Пуассона это упругая характеристика материала и...
+ представляет модуль отношения относительной и поперечной деформаций
53. Вторая теория прочности основана на ограничении...
+ наибольших линйных относительных деформаций
54. Третья теория прочности основана на ограничении...
+ наибольших касательных напряжений
55. Четвёртая теория прочности основана на ограничении...
+ удельной потенциальной энергии деформации
56. Осевой момент инерции сечения относительно оси y вычисляется по формуле...
+ 
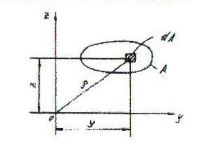
57. Полярный момент инерции сечения относительно точки О вычисляется по формуле...
+ 
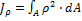
58. Центробежный момент инерции сечения относительно оси y и z вычисляется по формуле...
+ 
59. Статический момент сечения относительно оси z вычисляется по формуле...
+ 
60. Осевой момент инерции сечения относительно оси z вычисляется по формуле...
+ 
61. При переходе от осей координат y и z к осям y1 и z1, повернутым на угол α относительно начала координат, выполняется равенство...
+ 
62. При переходе от центральных осей кординат y и z к параллельным осям y1 и z1, находящимся от осей y и z на расстоянии a и b соответственно, осевой момент инерции относительно оси y1 вычисляется по формуле...
+ 
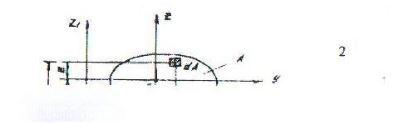
63. При переходе от централных осей координат y и z к параллельным осям y1 и z1, находящимся от осей y и z на расстоянии a и b соответственно, осевой момент инерции относительно оси z1 вычисляется по формуле...
+ 
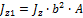
64. При переходе от централных осей координат y и z к параллельным осям y1 и z1, находящимся от осей y и z на расстоянии a и b соответственно, центробежный момент инерции относительно осей y1 и z1 вычисляется по формуле...
+ 
65. Осевой момент инерции кругового сечения относительно центральной оси z вычисляется по формуле...
+ 
66. Полярный момент инерции кругового сечения относительно центра тяжести сечения С определяется по формуле...
+ 
67. Верным является утверждение...
+ относительно главных осей центробежный момент инерции равен нулю
68. Угол поворота 
на который необходимо повернуть произвольные оси y и z, чтобы они стали главными осями, определяется по формуле...
+ 
+ 
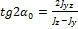
69. Главными центральными осями называются...
+ главные оси, проходящие через центр тяжести сечения
70. Верным является утверждение...
+ Относительно главных осей осевые моменты инерции принимают экстремальные значения
71. Пусть известны главные моменты инерции 
, 
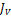и площадь сечения А, тогда главные радиусы инерции 
, 
определяются по формулам...
+ 
; 
72. Статический момент площади заданного сечения относительно оси y равен... 
+ 24 π см3
73. Координаты центра тяжести площади заданного сечения равны...
+ yc = 0, zс = 3,1 см
74. Осевой момент инерции треугольного сечения относительно центральной оси у, параллельной одной из сторон сечения определяется по формуле...
+ 
75. Осевой момент инерции треугольного сечения относительно центральной оси у, проходящей по одной из сторон сечения определяется по формуле...
+ 
76. Осевой момент инерции кругового сечения относительно центральной оси у, вычисляется по формуле...
+
77. Осевой момент инерции прямоугольного сечения относительно центральной оси у, вычисляется по формуле...
+
78. Осевой момент инерции прямоугольного сечения относительно центральной оси у и z, вычисляется по формуле...
+ 
79. Центробежный момент инерции прямоугольного сечения относительно осей y и z, вычисляется по формуле...
+ 
80. Осевой момент инерции прямоугольного сечения относительно центральной оси у, проходящей по стороне сечения вычисляется по формуле...
+ 
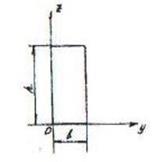
81. Осевой момент инерции прямоугольного сечения относительно центральной оси z, проходящей по стороне сечения вычисляется по формуле...
+ 
82. Центробежный момент инерции прямоугольного сечения относительно осей y и z, проходящих по сторонам сечения, вычисляется по формуле...
+ 
83. Положение центра тяжести сложного сечения устанавливается на основе понятия...
+ статического момента площади
84. Среди геометрических характеристик плоских сечний отрицательные значения может принимать...
+ центробежный момент инерции
85. Координаты центра тяжести сечения определяются по формулам...
+ 
; 
;
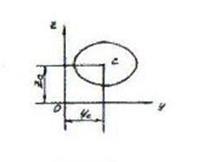
86. Координата 
центра тяжести составного сечения равна...
+ 
87. Координата центра тяжести составного сечения равна...
+ 
88. Координата 
центра тяжести составного сечения равна...
+ 
89. Для прямоугольного сечения главные оси инерции показаны на рисунке...
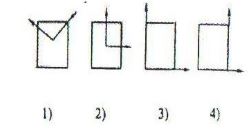
+ 2
90. Статический момент сечения относительно оси y вычисляется по формуле...
+ 
1.записать уравнение для определения прогиба балки при плоском изгибе: 
2. определить максимальное нормальное напряжение сигма мах при плоском поперечном
изгибе: 
3. какие граничные условия необходимо поставить для балки при плоском изгибе
4.какие граничные условия необходимо поставить для балки при плоском параллельном изгибе
5.подобрать необходимые размеры сечения балки
6. определить критическую силу по формуле Эйлера
7, подобрать необходимые размеры поперечных сечений балки 
8.определить лямбда предельную гибкость стержня 
9. как определяется жесткость балки при плоском поперечном изгибе
10. подсчитать величину обобщенной функции
11. приближенное дифференциальное уравнение изогнутой оси балки при плоском поперечном изгибе имеет вид 
12.какая из приведенных формул является формулой Ясенского
13. определить величину обобщенной функции 
14.которое из следующих выражений используется при расчете балок на прочность 
15. записать формулу для определения касательного напряжения формула журавского
16.определить максимальное нормальное напряжение при плоском поперечном изгибе
360? Не понятно))
17. определить касательное напряжение в точке 2
18. определить наименьшую гибкость стержня
92,3
19.определить величину критической силы
20. записать формулу для определения гибкости стержня
21. предельная гибкость стержня зависит только от
22. записать уравнение для обобщенного момента при плоском … бла бла
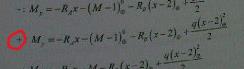
23. определить величину наибольшего по абсолютной величине прогиба для балки
24. определить критическую силу по формуле Эйлера
25.Признаком потери устойчивости сжатого стержня является
26.При сжатии упругого стержня показанного на рисунке … форма потери устойчивости стержня имеет вид
27. формула Эйлера для критической силы имеет вид
28. при изменении l и d величина критического напряжения будет изменятся
29.для определения критической нагрузки используется формула: ясинского
30. согласно эпюре М наиболее вероятным является вид упругой линии
31.в случае чистого плоского изгиба балки и ее …
32. к характеристике нулевой линии при плоском поперечном изгибе не относятся то что
33. полный расчет балки при плоско изгибе не требует выполнения
34. максимальный внутренний изгибающий момент имеет место в сечении
35.дифференциальное уравнение балки служит
36.согласно эпюре изгибающего момента М
37.в универсальных уравнениях изогнутой оси балки для определения начальных параметров необходимо удовлетворить граничные условия вида
38.уравнение 
служит для определения перемещений поперечных сечений бруса в случае: ПЛОСКОГО ИЗГИБА
39. Слой.. не меняющий своей длины при изгибе балки НЕЙТРАЛЬНЫЙ СЛОЙ
40. Установить правильное значение в формуле при вычислении напряжения в точке А заданного сечения 
41.как изменится численное значение критической силы по формуле Эйлера если оба конца стержня закрепить жесткими заделками
42. Чему равен угол поворота
43.чему равен прогиб на конце консоли
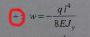
44. как изменится численное значение критической силы по формуле Эйлера для стержня если абсолютно жесткие заделки заменить на шарнирные крепления
45.чему равно нормальное напряжение в центре тяжести прямоугольного сечения балки
46. чему равно нормальное напряжение в т.А прямоугольного сечения балки при изгибе сигма=40
47. чему равно нормальное напряжение в т.А прямоугольного сечения балки при изгибе сигма=20
48.на каком участке указанной балки возникает чистый изгиб
49.Как изменится численно значение критического напряжения сигма по формуле Эйлера для стержня
50. на каком участке указанной балки возникает чистый изгиб
51. на каком участке балки возникает чистый изгиб
52. чему равно касательное напряжение а т.А прямоугольного сечения балки при изгибе =10мпа
53.Чему равно нормальное напряжение в т.В треугольного сечения балки
54. Отметить мах W максимальный по модулю прогиб при плоском поперечном изгибе
-Определить max |W|(максимальный по модулю прогиб)при плоском поперечном изгибе:
EJy=const
+ 
-Определить предельная гибкость стрежня и гибкость стержня
l=1м 
Е= 2*1011 Па R =2 см
+пред=91, гибкость=100
-Определить гибкость стержня если l=1м h=b=3 см
+163
-Вид нагружения бруса когда в поперечном сечении бруса определено действуют несколько внутренних усилии называется
+сложным сопротивлением
-Для определения нагружения при сложном сопротивлении используется
+принцип суперпозиции
-Пространственный изгиб вызывается
+моментами расположенными в различных плоскостях проходящих через ось балки
+Вид пространственного изгиба когда нагрузки лежат в одной плоскости не совпадающей ни с одной из главных плоскостей называется
+косым изгибом
-При пространственном изгибе нормальные напряжения определяются по формуле
+ 
-При косом изгибе нормальные напряжения определяют по формуле
+ 
-Геометрическое место точек сечения в которых нормальные напряжения равны нулю
+ нейтральная линия
-Если при действии нескольких изгибающих моментов Jy=Jz, то имеет место
+плоский изгиб
-Если при косом изгибе Jy не равен Jz, то нейтральная линия
+не перпендикулярна силовой линий
- Направление полного прогиба при косом изгибе
+ перпендикулярно нейтральной линии
- Положение силовой линий при косом изгибе определяется
+ 
- 
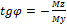
при косом изгибе справедлива для сечения в виде
+ прямоугольник
-Полный прогиб при неплоском изгибе определяется как
+ w=wz 
2 
-Внецентренное растяжение представляет собой частный случай
+ изгиба с растяжением
-При внецентренном растяжений
+ zN = 
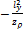yN=- 
- Данный вид нагружения представляет
+внецентренное растяжение
- …..=-1 – уравнение нулевой линий при
+ внецентренном растяжении
-Положение нулевой линии при внецентренном изгибе зависит от
+ положении полюса и геометрии сечения
-Ядром сечения называется область вокруг центра тяжести поперечного сечения
+если нагрузка расположена в области ядра то нормальные напряжения во всех точках поперечного сечения имеют один знак
-При повороте нейтральной линии вокруг фиксированной точки контура сечения
+ точка приложения силы перемещается вдоль некоторой прямой
-По формуле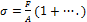 
определяется напряжение при
+ внецентренном растяжении
-При расчете на прочность при изгибе кручением используется
+определенная теория прочности
-Для бакли определить величину наибольших нормальных напряжений.
- Для бакли определить величину наибольших нормальных напряжений.
- Для бакли определить величину наибольших нормальных напряжений.
- Для бакли определить величину наибольших нормальных напряжений.
- Для бакли определить величину наибольших нормальных напряжений.
Для бакли определить величину наибольших нормальных напряжений.
-Произвольная сила и изгибающие моменты в опасном сечении балки соответственно равны
-Вид сложного кручения представляет собой
+изгиб с кручением
- В сечении А-А опасным являются точки
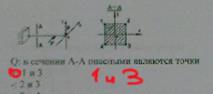
-Условие прочности стержня имеет вид
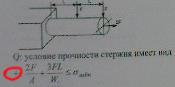
-Нормальное напряжение в точке С равно
-Вид сложного сопротивления представляет собой
+внецентренное растяжение
-Наиболее опасной является
+точка 3
-Нейтральная линия есть прямая
+2-2
-Опасным являются точки
- Вид сложного сопротивления представляет собой
-Допускаемая нагрузка из условия прочности имеет вид
- Вид сложного сопротивления представляет собой
-Из условия прочности
-Нейтральной линией является линия
-Наибольшее нормальное напряжение в опасном сечении равно
-Положение нейтральной линии в опасном сечении с горизонтальной Осью у
-Как расположены полное и нейтральная линия при внецентренном сжатии
+по разные стороны от центра тяжести
-Если полное при внецентренном сжатии лежит на одной из главных осей сечений то нейтральная линия
+ параллельна другой главной оси
-При внецентренном растяжении нейтральная линия
+может проходить через ц т при соответствующем положении полюса
-На положение нейтральной линии при внецентренном сжатии не влияет
+значение и знак внешней нагрузки
-Максимальные напряжения при внецентренном растяжении возникают в точках поперечного сечения
+наиболее удаленных от нейтральной линии
-При изгибе с кручением имеет место плоское напряженное состояние
-Условие прочности по третьей теории прочности при изгибе с кручением для круглых брусьев имеет вид
-Условие прочности по четвертой теории прочности при изгибе с кручением для круглых брусьев имеет вид
-Значение допускаемой нагрузки
-При косом изгибе для прямоугольного сеения
1)Определить max|Wy|(максимальный по модулю прогиб)при плоском поперечном сечении изгибе EJy=const
+ 
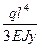
2)Определить 
(предельная гибкость стержня) и 
(гибкость стержня) при:l=1м, 
=1
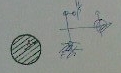
=240ПА Е=2*10^11 R=2см. + =91, =100
3)Определить (гибкость стержня) если l=1м,h=b=3см.
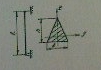+ 163
4)Положение силовой линии при косом изгибе определяется
+ 
5) 
при косом изгибе справедлива для сечения в виде:
+ прямоугольника
6)Полный прогиб при неплоском изгибе определяется как
+ W= 
7)Внецентровое растяжение представляет собой частный случай
+ изгиба напряжения
8)При внецентренное растяжение
+ 
9)Вид нагружения бруса,когда в поперечном сечении бруса одновременно действуют несколько внутренних усилий,называется
+ сложным сопротивлением
10)Для определения напряжений при сложном сопротивлении используется
+ принцип суперпозиции
11)Пространственный изгиб вызывается
+ моментами, расположенных в разных плоскостях проходящих через ось балки.
12)Вид пространственного изгиба кода нагрузки лежат в одной плоскости,не совпадающей ни с одной из главных плоскостей,называется
+ косым изгибом
13)При пространственном изгибе нормальные напряжения определяются по формуле
+ 
14)Данный вид нагружения представляет собой
+ внецентровое растяжение 
15) 
уравнение нулевой линии при:
+ Внецентровом растяжении
16) положение нулевой линии при внецентровом изгибе зависет от
+ положения полюса и гометрии сечения
17)Ядром сечения называется область вокруг центра тяжести поперечно сечения,которая обладает следующими свойствами%
+ если нагрузка расположена в области ядра,то нормальные напряжения во всех точках поперечного сечения имеют один знак
18)При повороте нейтральной линии вокруг фиксированной точки контура сечения
+ точка приложения силы перемещается вдоль некоторой прямой
19)По формуле 
определяется напряжение при
+ внецентренном растяжении
20)Как измениться численное значение критической силы по формуле Эйлера для стержня если абсолютно жесткие заделки заменить на шарнирные закрепления?
+ уменьшиться в 4 раза
21)Как измениться численное значение критической силы по формуле Эйлера,если оба конца стержня закрепить жесткими заделками?
+ увеличиться в 16 раз
22)Чему равен угол поворота на конце консоли от заданной нагрузки?EJy=const
+ 
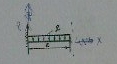23)Чему равен прогиб на конце консоли от заданной нагрузки?EJy=const
+ 
24)При расчете на прочность при изгибе с кручением используется
+Определенная теория прочности
25)Эквивалентные напряжения при изгибе с кручением по третьей теории прочности
+ 
26)Для балки определить величину наибольших нормальных напряжений.В расчетах принять сечение –прямоугольник с соотношением сторон h:b=2:1,P=20H,l=1м,b=1см.
+ 120 МПА
27)Для балки определить величину наибольших нормальных напряжений.В расчетах принять:сечение прямоугольник с соотношением сторон h:b=2:1,P=200H,L=1м,b=2cm,M=12
+ 150МПА
28)Для балки определить величину наибольших нормальных напряжений.В расчетах принять сечение: прямоугольник с соотнеошением сторон h:b=2:1,P=300H,L=1m,b=2.3cm,M=PL
+ 192 МПа
29) Для балки определить величину наибольших нормальных напряжений.В расчетах принять сечение: прямоугольник с соотнеошением сторон h:b=2:1,P=22H,L=1m,b=3cm,M=PL
+ 167 МПа
30) Для балки определить величину наибольших нормальных напряжений.В расчетах принять сечение: прямоугольник с соотнеошением сторон h:b=2:1,P=2кН,L=1m,b=1cm,q=p\2
+ 167 МПа
31) Для балки определить величину наибольших нормальных напряжений.В расчетах принять сечение: прямоугольник с соотнеошением сторон h:b=2:1,P=2kH,L=1m,b=3cm,M=pl
+ 150 МПа
32)Продольная сила и изгибающие моменты в опасном сечении балки соответственно равны:
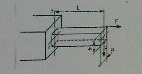+ N=F,M1=F1,M2=FL+2Ft
33)Чему равно нормальное напряжение в центре тяжести прямоугольного сечения балки при плоском поперечном изгибе,если в этом сечении adm=10МПа
=0
34)Чему равно нормальное напряжение в точки А прямоугольного сечения балки при плоском поперечном изгибе,если в этом сечении adm=40МПа
=20МПа
35)Чему равно нормальное напряжение в точке А прямоугольного сечения балки при изгибе,если в этом сечении нач=20МПа
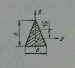
а=10МПа
36)На каком участке указанной балки возникает чистый изгиб
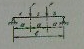+ на участке 2
37)Как измениться численное значение критического напряжения кр.по формуле Эйлера для стержня,если шарнирные крепления его концов заменить абсолютными жесткими заделками
+ увеличится в 4 раза
38) На каком участке указанной балки возникает чистый изгиб
+на участке 3
39)К характеристике нулевой линии при плоском поперечном изгибе не относитсься то что
+ Она представляет след силовой плоскости в поперечном сечении
40)Полный расчет балки при плоском изгибе не требует выполнения
+ условия продольной устойчивости
41)Максимальный внутренний изгибающий момент имеет место в сечениях
+ В
42)Дифференциальное уравнение изгиба балки служит
+ Для определения поперечных перемещений и углов поворота поперечных сечениях
43)Согласно эпюре изгибающего момента М наиболее вероятным является вид упругой линий(Изогнутой оси) балки:
+ 1
44)Вид сложного сопротивления представляет собой
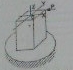+ изгиб с кручением
45) В сечениях А-А опасными являются точки
+ 1и 3
46)Условие прочности стержня имеет вид
47)На каком участке указанной балки возникает чистый изгиб
+ на участке 3
48)Чему равно касательное напряжение в точке А прямоугольного сечения балки при изгибе,если в этом сечении 
доп=10МПа
а=7.5 МПа
49) Чему равно нормальное напряжение в точке В треугольного сечения балки при изгибе если растягоивающее напряжение в точке А равно 60МПа
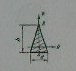
а=-30МПа
50)Определить max|Wz|(максимальный по модулю прогиб)при плоском поперечном изгибе EJy=const
+ 
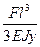
51) Записать уравнение для определения прогиба балки (EJy=const) при плоском изгибе:
Ra(x-a)3/6 + M(x-b)2/2 – q(x-b)4/24 + C1x+ C2
52) Определить Gmax (максимальное нормальное напряжение) при плоском поперечном изгибе:
6Fl/bh2
53) Какие граничные условия необходимо поставить для балки при плоском изгибе:
Wz(L)=0; Q(L)=0 
54) Какие граничные условия необходимо поставить для балки при плоском изгибе:
Wz(0)=0; Q(0)=0; 
55)Какие гранчные условия необходимо поставить для балки при плоском постоянном изгибе
Wz(L1)=0; Wz(L1+L2)=0 
56) Подобрать необходимые размеры сечения балки:
Корень из 3ех (см)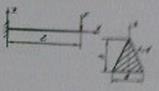 
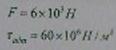
57) Определить критеческую силу по формуле Эйлера. Сечения сержня со стороной а.
Fкр=pi2a2E/4800
58) Подобрать необходимые размеры поперечных сечений балки:
0,079м
59) При косом изгибе нормальные напряжения определяют по формуле:
60) Геометрическое место точек сечения в которых нормальные напряжения равны нулю:
Нейтральная линия
61) При косом изгибе уравнение нейтральной линии имеет вид:
62)Если при действии нескольких изгибающих моментов Jy = Jz то имеет мечто:
Плоский изгиб
63)Если при косом изгибе Jy≠Jz то нейтральная лини:
