Нейтральная линия
61) При косом изгибе уравнение нейтральной линии имеет вид:
62)Если при действии нескольких изгибающих моментов Jy = Jz то имеет мечто:
Плоский изгиб
63)Если при косом изгибе Jy≠Jz то нейтральная лини:
Не перпендикулярна силовой
64)Направление полного прогиба при косом изгибе:
Перпендикулярна нейтральной линии
65) В универсальных уравнениях изогнутой оси балки для определения начальных параметров необходимо удовлетворить граничным условием вида:
Wz(a)=0; Wz(a+b)=0; 
66)Уравнение 
служит для определения перемещений поперечных сечений бруса в случае:
Плоского изгиба
67)Слой волокон, не меняющий своей длины при изгибе балки называется:
Нейтральным слоем
68 ) Установить правильное значение My, z, J по формуле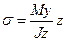 
при вычислении напряжения в точке А
69)При внецентренном растяжении нейтральная лини:
Может проходить через o.y. при соответствующем положении полюса.
70)На положение нейтральной линии при внецентренном сжатии не влияет:
Значение и знак внешней нагрузки
71) максимальные напряжение при внецентренном растяжении возникают в точках поперечного сечения:
Наиболее удаленных от нейтральной линии
72) При изгибе с кручением имеет место ……. Напряженное состояние.
Плоское
73) условие прочности по третьей теории прочности при изгибе с кручением для круглых брусьев имеет вид:
74) условие прочности по четвертой теории прочности при изгибе с кручением для круглых брусьев имеет вид:
75)нейтральной линией является линия
2-2 
76) наибольшее нормальное напряжение в опасном сечении равно:
9,5 МПа 
77)положение нейтральной линии в опасном сечении с горизонтальной Осью у определяется углом
α=61,6 
78) Как расположены полюс и нейтральная линия (N-N) при внецентренном сжатии:
По разные стороны от центра тяжести
79) если полюс при внецентренном сжатии лежит на одной из главных осей сечения, то нейтральная линия N-N
Параллельна другой главной оси
80) Приближенное дифференциальное уравнение изогнутой оси балки при плоском поперечном изгибе имеет вид:
81) какая из приведенных формул является формулой Ясинского для критических напряжений (a, b – const) λ – гибкость стержня
82) Определить велечину обобщенной функции: y=(x-1)+(x-13)2+(x-17)3+(x-9)4+(x-11)4+(x-12)5 при х = …
y=10
83) Которое из след. Выражений используется при расчете балок на прочность при плоском поперечном изгибе по максимальным нормальным напряжениям
84) Определить λпр – предельную гибкость стержня, Fкр – величину критической силы:
λкр=91 Fкр=430Н 
85)Как определяется жесткость балки при плоском поперечном изгибе
EJy
86) Вычислить велечину обобщенной функции y=x(x-2)2+(x-5)3+(x-5)4
y=8
87) Определите какая из формул является формулой для определения нормальных напряжений при плоском поперечном изгибе балок:
??????????????????????????
88)Определить величину наибольшего по абсолютной величине прогиба для балки при плоском поперечном изгибе,если E=2*10^11ПА,Jy=5000cm^4,L=3m,F=30kH
+2.7cm
89)Определить критическую силу по формуле Эйлера
+ 
90)Признаком потери устойчивости сжатого стержня является
+внезапная смена прямолинейной формы равновесия на криволинейную
91)При сжатии упругого стерженя,показанного на рисунке силой F>=Fкр форма потери устойчивости имеет вид
+2
92)Формула Эйлера для критической силы имеет вид
+ 
93)Значение допускаемой нагрузки(
adm=10МПа)равно
+1.6 кН
94)При косом изгибе для прямоугольного сечения (h*b)
+ 
95)Определить формулу для определения касательных напряжения при плоском поперечном изгибе(формулу Журавского)
+ 
96)Определить максимальное нормальное напряжение при плоском поперечном изгибе.Дано Му=20.8кН,h=12cm,h0=8cm,b=6cm,b0=4cm
+180МПа
97)Определить касательное напряжения в точке 2,если ширина сечения равна b=6cm.Дано Qл=80кн,h=12cm,h0=8cm,b=6cm,b0=4cm
+ 
=11,54МПа
98)Опоределить измененную гибкость стержня при которой ещё применяется формула Эйлера для критической силы,если предел пропорциональности 
=2200кг\см4,модуль упругости E=1.9*10^4кг\см2
+92.3
99)Определить величину критической силы для сжатой стойки квадратоного сечения стороной а.Оба конца шарниро закреплены
+ 
100)Допускаемая нагрузка из условии прочности имеет вид
+ 
101)Вид сложного сопротивления представляет собой
+косой изгиб
102)Из условия прочности 
F удовлетроряет неравенству
+ 
103)Записать формулу для определения гибкости стержня
+ 
104)Предельная гибкости стержня зависит только от
+материала из которого изготовлен стержень
105) Записать уравнение для обощенного момента при плоском поперечном изгибе для балки
+My=-RaX-(M-1)^0-R0(x-2)+q(x-2)^2\2
106)(
>= пред)при изменении l и d величина керического напряжения будет изменяться пропорционально отношению
+d\l
107)Для определения критической нагрузки за пределом пропорциональности используется формула
+Ясинского
108)Согласно Эпюре М наиболее веороятным является вид упругой (изогнутой оси) балки
+3
109)В случае чистого плоского изгиба балки и ее поперечных сечений из части внутренних силовых факторов отличных от нуля
+изгибающий момент-М
110)Опасными являются точки
+А и С
111)Вид сложного сопротивления представляет собой
+общий случай сложного сопротивления
112)Нормальное напряжение в точке С равно
+ 
113)Вид сложного сопротивления представляет собой
+изгиб с кручением
114)Наиболее опасным является
+точка 3
115)Нейтральная линия есть прямая
+2-2
Закон Гука справедлив до напряжения соответствующему:
+: пределу пропорциональности материала
Коэффициент Пуассона для известных конструкционных материалов находится в пределах:
+: 0 ν 0, 5
Какая связь существует между упругими константами – модулем сдвига G, модулем Юнга Е и коэффициентом Пуассона ν:
+: G=E/2(1+ν)
Способность твердого тела сопротивляться внешним нагрузкам не разрушаясь (способность сопротивляться разрушению) называется:
+: прочностью
Предел отношение равнодействующей Р внутренних сил, действующих на площадку А, к величине площади А, когда последняя стремится к нулю определяет величину вектора:
+: полного напряжения
К основным гипотезам сопротивления материалов не следует относить:
+: гипотезу об идеальной теплопроводности
Для определения внутренних силовых факторов в поперечных сечениях нагруженного бруса нужно:
+: составить уравнение равновесия для одной из частей
Чистый сдвиг является частным случаем:
+: плоского напряженного состояния
При расчёте на прочность, ограничиваются максимальные значения:
+: напряжений
Все известные теории прочности приводят к одинаковым результатам:
+: при растяжении стержней
Вектор полного напряжения на данной площадке р раскладывают на составляющие (на нормаль к площадке и на плоскость этой площадки) Эти составляющие называют:
+: нормальными и касательными напряжениями
Изменение положения в пространстве одного тела (или частицы тела) относительно другого тела в различные фиксированные моменты времени называются:
+: перемещением
Внутренние силовые факторы в поперечных сечениях бруса не зависит от:
+: размеры и формы сечения
Сколько внутренних силовых факторов возникает в поперечных сечениях стрежня в общем случае нагружения:
+: Шесть
Какая гипотеза положена в основу теории растяжения (сжатия) прямолинейных стержней:
+: гипотеза плоских сечения
Изотропным материалов не является:
+: древесина
Внутренние силовые факторы в сечениях нагруженных объектов определяются с помощью:
+: метода сечений
В основном объектами изучения сопротивления материалов является:
+: элемента в виде бруса конструкции из них
Условие прочности в энергетической теории прочности представляется неравенством:
+: корень ½ (….) <…
Из классификации напряженного состояния нужно исключить понятие:
+: общего напряженного состояния
К характеристики внутренних напряжений не относится утверждение о том, что они:
+: не связаны с деформациями
Расчёт на прочность и жёсткость в условиях сложного сопротивления (сложной деформации) производится на основе:
+: принципа суперпозиции
Первая теория прочности основана на ограничении:
+: наибольших растягивающих нормальных напряжений
В нагруженном твёрдом теле напряжения в общем случае не зависит от:
+: материала
Коэффициент Пуассона это упругая характеристика материала и:
+: представляет модуль отношения относительной и поперечной деформаций
Вторая теория прочности основана на ограничении:
+: наибольших литейных относительных деформаций
Третья теория прочности основана на ограничении:
+: наибольших касательных напряжений
Четвёртая теория прочности основана на ограничении:
+: удельной потенциальной энергии деформации
Изменение размеров или формы тела под действием внешних сил называется:
+: деформированным состоянием
Материал называется изотропным, если:
+: свойства образца выделенного из материала, не зависит от его угловой ориентации
Пластичностью называется свойство материала:
+: сохранять некоторую часть деформации после снятия нагрузки
Способность тела под нагрузкой сохранять заданную (первоначальную) форму равновесия называется:
+: устойчивостью
К характеристики главных площадок нельзя отнести:
+: число таких площадок в каждой точке нагруженного объекта может быть неограниченным.
Осевой момент инерции прямоугольного сечения относительно центральной оси zвычисляется по формуле:
+: J=hb3/12
Центробежный момент инерции прямоугольного сечения относительно оси yиzпоказанных на рисунке, вычисляется по формуле:
+: J=0
Осевой момент инерции прямоугольного сечения относительно оси y, проходящей по стороне сечения вычисляется по формуле:
+: J= bh3/3
Осевой момент инерции прямоугольного сечения относительно оси z, проходящей по стороне сечения вычисляется по формуле:
+: J=hb3/3
Центробежный момент инерции прямоугольного сечения относительно осей yиz, проходящих по сторонам сечения, вычисляется по формуле:
+: J=b2h2/4
Положение центра тяжести сложного сечения устанавливается на основе понятия:
+: статического момента площади
Среди геометрических характеристик плоских сечений отрицательные значения может принимать:
+: центробежный момент инерции
Координаты центра тяжести сечения определяются по формуле:
+: z=S1/A, y=S1/A
Удельная потенциальная энергия упругой деформации вычисляется по формуле:
+: u=..1E1+..2E2+..3E3 / 2
Первая классическая теория прочности имеет вид:
+:..1<..
Вторая классическая теория прочности имеет вид:
+:..1-v(..2-..3)<..
Третья классическая теория прочности имеет вид:
+:..1-..3<..
Четвёртая теория прочности имеет вид:
+: корень из ½ (…)<…
Касательное напряжение не:
+: вызывают изменение объёма нагруженного твёрдого тела
В случае объёмного напряженного состояния максимальные касательные напряжения в точках нагруженного объекта можно определить как:
+:..-.. / 2
Главная относительная линейная деформация это:
+: деформация в направлении главного напряжения
Обобщенный закон Гука это:
+: самый большой ответ
Действие угловых напряжений показано на рисунке:
+: 4
Формула для определения угла закручивания в произвольном сечении стержня с круглым сечением при ф=0, постоянном крутящем моменте Ти постоянной жесткостиGJpимеет вид:
+: ф(х)=Tx/GJр
Формула для определения угла закручивания стержня с круглым сечением, накапливаемого на отдельном участке при, постоянном крутящем моменте Ти постоянной жесткости имеет вид:
+: ф(х)= Tl/GJр
При кручении в поперечных сечениях вала из шести внутренних силовых факторов отличен от нуля:
+: крутящий момент Т
Формула для вычисления касательных напряжений, возникающих в поперечных сечениях стержня с круглым сечением при кручении имеет вид:
+: Тр/Ip
Модуль упругости материала является:
+: мерой жесткости материала
Предел текучести материала это:
+: напряжение, при достижении которого деформация увеличивается без увеличения напряжения
Предел упругости материала представляет:
+: максимальное напряжение, при превышении которого материал получает необратимую деформацию
В данном случае относительная продольная деформация в точках стержня определяется согласно формуле:
+:E(x)=-N(x)/EA
Осевой момент инерции сечения относительно оси у вычисляются по формуле:
+:Jy = интегралz2*dA
Полярный момент инерции сечения относительно точки О вычисляются по формуле:
+: Jp = интегралp2*dA
Центробежный момент инерции сечения относительно осей у и zвычисляется по формуле:
+: Jyz = интегралy*z*dA
Чугун и сталь – материалы:
+: изотропные
В сечении 1-1имеют место внутренние силовые факторы:
+: М и Qне равны 0 на чертеже есть данные 2в,в,в
В поперечном системе стержня, изображенного на рисунке действуют внутренние силовые факторы:
+: Mzи Qy
В сечении 1-1 имеет место внутренние силовые факторы:
+: М не равно 0, Q=0 на чертеже есть данные 2а,2а
Упругостью называется свойство материала:
+: восстанавливать свою форму и размеры после снятия нагрузки
В модели формы при расчётных прочностной надёжности вводят упрощения в геометрию элементов конструкций, приводя их к схеме…
+: стержня (бруса),пластинки, оболочки и массива (пространственного тела)
Предел отношения liml/t называется…
+: относительной линейной деформацией в точке
Компонент вектора полного напряжения р, действующего в некоторой точке сечения тела, определяемый проекцией вектора р на плоскость сечения называется:
+: касательным напряжением r
Какие основные задания решаются в курсе сопротивления материалов:
+: задача, прочности, жесткости, устойчивости
Жесткость называется:
+: способность тела воспринимать воздействия внешних сил без существенного изменения геометрических размеров
Главные напряжения связаны между собой следующим соотношением:
+:..1>..2>..3
Закон Гука справедлив до напряжения соответствующему …
пределу пропорциональности материала
Коэффициент Пуассона для известных конструкционных материалов находится в пределах:
+: 0 
ν 0, 5
Какая связь существует между упругими константами – модулем сдвига G, модулем Юнга Е и коэффициентом Пуассона ν?
+: G=E/2(1+ν)
Способность твердого тела сопротивляться внешним нагрузкам не разрушаясь (способность сопротивляться разрушению) называется…
Прочностью
Предел отношение равнодействующей Р внутренних сил, действующих на площадку А, к величине площади А, когда последняя стремится к нулю определяет величину вектора
Полного напряжения
К основным гипотезам сопротивления материалов не следует относить…
