Фактором называется измеряемая переменная величина, принимающая в некоторый момент времени определенное значение. Так же, как и параметр оптимизации, каждый фактор имеет область определения. Фактор считают заданным, если вместе с его названием указана область его определения.
Под областью определения понимается совокупность всех значений, которые в принципе может принимать данный фактор.
Совокупность значений фактора, которая используется в эксперименте, является подмножеством из множества значений, образующих область определения. Область определения может быть непрерывной и дискретной. Однако в основном, в задачах планирования эксперимента, используются дискретные области определения. Так, для факторов с непрерывной областью определения, таких, как температура, время, количество вещества и т.п., всегда выбираются дискретные множества уровней.
В практических задачах области определения факторов, как правило, ограничены. Ограничения могут носить принципиальный либо технический характер.
Графическое отображение области определения факторов
Для факторов существуют области определения. Это значит, что у каждого фактора есть минимальное и максимальное возможные значения, между которыми он может изменяться либо непрерывно, либо дискретно. Если факторы совместимы, то границы образуют на плоскости некоторый прямоугольник, внутри которого лежат точки, соответствующие состояниям «черного ящика». Пунктирными линиями на рисе обозначены границы областей определения каждою из факторов, а сплошными – границы их совместной области определения.
Матрица планирования.
План полного факторного эксперимента изображают в виде таблицы, столбцы которой отражают уровни факторов, а строки – номера опытов. Эти таблицы называют матрицами планирования эксперимента. Поскольку значения уровней факторов по модулю всегда равны единице, то обычно в МП записывают только знак уровня (т. е. «+» вместо «1» и «–» вместо «–1»).
Матрица планирования для двух факторов приведена табл. 1:
Таблица 1 Таблица 2
| № эксп. | x1 | x2 | y | № эксп. | x1 | x2 | x3 | y | |
| - | - | y1 | - | - | - | y1 | |||
| + | - | y2 | + | - | - | y2 | |||
| - | + | y3 | - | + | - | y3 | |||
| + | + | y4 | + | + | - | y4 | |||
| - | - | + | y5 | ||||||
| + | - | + | y6 | ||||||
| - | + | + | y7 | ||||||
| + | + | + | y8 |
Если для двух факторов все возможные комбинации уровней легко найти прямым перебором, то с ростом числа факторов возникает необходимость в некотором приеме построения матриц. Рассмотрим прием, основанный на правиле чередования знаков. В первом столбце знаки меняются поочередно, во втором столбце они чередуются через два, в третьем – через 4, в четвертом – через 8 и т. д. по степеням двойки. Так, для трехфакторного эксперимента (табл. 2).
Влияние факторов на функцию отклика может зависеть от уровня другого фактора, или от сочетания уровней нескольких факторов. Если априорно неизвестно, что такой зависимости между факторами нет, то строят развернутую матрицу планирования, учитывающую не только факторы, но и их взаимодействия. При этом знаки в столбцах для взаимодействий получают перемножением знаков взаимодействующих факторов. Для удобства расчета свободного члена a0 математической модели в матрицу вводят фиктивный фактор x0.
15. Свойства матрицы планирования эксперимента:
1) Симметричность относительно центра эксперимента. Это значит, что алгебраическая сумма элементов вектор-столбца для каждого фактора равна 0, т. е. 
, где j — номер фактора (j=1, 2,,.., k ), i — номер опыта (i=1, 2,..., N).
2) Условие нормировки — формулируется след образом: сумма квадратов элементов каждого столбца равна числу опытов, т. е. 
. Это следствие того, что значения факторов в матрице задаются в кодированном виде как +1 и -1.
3) Ортогональность сумма почленных произведений любых двух вектор-столбцов матрицы равна 0:
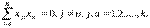
4) Рототабельность – точки в матрице планирования подбираются так, что точность предсказания значений параметра оптимизации одинакова на равных расстояниях от центра эксперимента и не зависит от направления.
Матрица, удовлетворяющая условиям симметричности, нормировки, ортогональности и рототабельности, называется оптимальной.
