Параболическая интерполяция.
Если интерполирующая функция - многочлен второго порядка 
, то интерполяция называется квадратичной. Иногда ее называют параболической на отрезке [ xi -1, xi +1], так как квадратный трехчлен - это парабола 
, где 
- неизвестные. Для их определения необходимо условие прохождения параболы через три точки: 
.
Графическая иллюстрация метода представлена на рис.1
Эти условия запишем в виде:
Решив систему, получим значения 
, а, следовательно, и уравнение параболы на участке [ xi -1, xi +1]. Уравнения парабол на разных отрезках [ xi -1, xi +1] разные.. 
Квадратичная интерполяция является локальной интерполяцией.
Интерполяционная формула Лагранжа.
Примером глобальной интерполяции является построение интерполяционного многочлена, единого для всего отрезка[ x 0, xn ], график которого проходит через все заданные в таблице точки. Это многочлен Лагранжа. Его уравнение имеет вид:
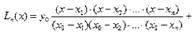
или
|
Где х - значение аргумента функции, расположенного в интервале [ x 0, xn ].
Необходимо отметить, что формула Лагранжа, в отличие от других интерполяционных формул, содержит явно yi(i = 
), что бывает иногда важно.
Интерполяционная схема Ейткина.
Наиболее известным из итерационных методов является метод Эйткена, в основе которого лежит многократное применение линейной интерполяции.
Схема Эйткена предлагает более удобную форму вычисления 
по формуле Лагранжа.
На первом этапе вычисляются многочлены 
,построенные на каждой паре соседних узлов:
, 
Затем на их основе вычисляются многочлены, построенные на тройках соседних узлов:
, 
и т.д., пока не получится один многочлен, построенный на всех узлах интерполяции:
Нетрудно убедиться, что 
.
Виды систем координат.
Декартовы прямоугольные системы координат
Декартовыми прямоугольными координатами точки P на плоскости называются взятые с определенным знаком расстояния этой точки до двух взаимно перпендикулярных прямых - осей координат или проекции радиус-вектора точки P на две взаимно перпендикулярные координатные оси.
Координаты x и y называются соответственно абсциссой и ординатой точки
Полярные системы координат
Полярными координатами точки P называются радиус-вектор ρ - расстояние от точки P до заданной точки O (полюса) и полярный угол φ - угол между прямой OP и заданной прямой, проходящей через полюс (полярной осью).
Координатные линии в полярных системах - окружности с центром в полюсе и лучи.
Формулы для перехода от полярных координат к декартовым
x=ρ*cos(φ), y=ρ*sin(φ)
Цилиндрические системы координат
Для цилиндрических координат координатными поверхностями являются плоскости, перпендикулярные к оси Oz (z=const), полуплоскости, ограниченные осью z (φ=const) и цилиндрические поверхности, осью которых является ось z (ρ=const). ρ и φ - полярные координаты проекции точки P на основную плоскость (обычно xOy), z - аппликата - расстояние от точки P до основной плоскости.
Формулы для перехода от цилиндрических координат к декартовым x=ρ*cos(φ), y=ρ*sin(φ), z=z
