1. В студенческом потоке 37 человек хорошо знают математику, а 25 человек – электронику, и 19 человек хорошо знают и математику и электронику. Если в потоке каждый из студентов знает хотя бы один из этих предметов, то сколько студентов в потоке?
2. Из 250 студентов 151 изучают немецкий язык, 136 – французский язык, 27 – итальянский, 63 – французский и немецкий, 7 – итальянский и французский, 11 – немецкий и итальянский, 4 – все три языка.
а) Сколько студентов изучают немецкий или французский язык?
б) Сколько студентов изучают только итальянский язык?
в) Сколько студентов изучают немецкий и французский язык, но не
итальянский?
г) Сколько студентов не изучают ни одного языка?
д) Сколько студентов изучают хотя бы два иностранных языка?
3. В отчете о количестве студентов, изучающих иностранные языки, сообщалось, что из 100 студентов все три языка изучают 5 человек, немецкий и английский – 10 человек, французский и английский – 8 человек, немецкий и французский – 20 человек, английский – 30, немецкий – 23, французский – 50. Инспектор, представивший этот отчет, был отстранен от работы. Почему?
4. Каждый из 500 студентов обязан посещать хотя бы один из трех спецкурсов: по математике, физике, астрономии. Три спецкурса посещают 10 студентов, по математике и астрономии –25 студентов, спецкурс только по физике – 80 студентов. Известно также, что спецкурс по математике посещают 345 студентов, по физике – 145, по астрономии – 100 студентов. Сколько студентов посещают спецкурс только по астрономии? Сколько студентов посещают два спецкурса?
5. Экзамен по математике содержал три задачи: по алгебре, геометрии и тригонометрии. Из 800 абитуриентов задачу по алгебре решили 250 человек; по алгебре или геометрии – 660 человек; по две задачи решили 400 человек, из них две задачи по алгебре и геометрии решили 150 человек, по алгебре и тригонометрии – 50 человек; ни один абитуриент не решил все задачи; 20 абитуриентов не решили ни одной задачи; только по тригонометрии задачи решили 120 человек. Сколько абитуриентов решили только одну задачу? Сколько абитуриентов решили задачи по тригонометрии?
6. На курсах иностранных языков учится 600 человек. Из них французский изучают 220 человек, английский – 270 человек. Слушатели, изучающие английский язык, не изучают немецкий язык; один французский язык изучают 100 человек, один немецкий язык изучают 180 человек. Сколько человек изучает по два иностранных языка? Сколько человек изучает один иностранный язык?
7. На кафедре иностранных языков работают 18 преподавателей. Из них 12 преподают английский язык, 11 – немецкий язык, 9 – французский язык. 5 преподавателей преподают английский и немецкий языки, 4 – английский и французский, 3 – немецкий и французский. Сколько преподавателей преподают все три языка? Сколько преподавателей преподают только два языка?
8. Группа студентов из 25 человек сдала экзаменационную сессию со следующими результатами: 2 человека получили только “отлично”; 3 человека получили отличные, хорошие и удовлетворительные оценки; 4 человека только “хорошо”; 3 человека только хорошие и удовлетворительные оценки. Число студентов, сдавших сессию только на “удовлетворительно”, равно числу студентов, сдавших сессию только на “хорошо” и “отлично”. Студентов, получивших только отличные и удовлетворительные оценки – нет. Удовлетворительные или хорошие оценки получили только 22 студента. Сколько студентов сдали сессию только на “удовлетворительно”?
9. Преподаватели кафедры Прикладной математики преподают на трех факультетах: механическом, технологическом, экономическом. На технологическом факультете работает 22 преподавателя, на механическом – 23 преподавателя, на механическом и экономическом –36 преподавателей.Только на технологическом факультете работают 10 преподавателей. 2 –на трех факультетах. 5 преподавателей работают только на механическом и экономическом факультетах. Число преподавателей, работающих только на механическом и технологическом факультетах, равно числу преподавателей, работающих на экономическом и технологическом факультетах. Сколько преподавателей работает на кафедре? Сколько преподавателей работает только на одном факультете?
10. Экзамен по математике содержал три задачи: по алгебре, геометрии и тригонометрии. Из 750 абитуриентов задачу по алгебре решили 400 абитуриентов, по геометрии – 480, по тригонометрии – 420. Задачи по алгебре или геометрии решили 630 абитуриентов; по геометрии или тригонометрии – 600 абитуриентов; по алгебре или тригонометрии – 620 абитуриентов. 100 абитуриентов не решили ни одной задачи. Сколько абитуриентов решили все задачи? Сколько абитуриентов решили только одну задачу?
Декартово произведение множеств. Соответствия. Бинарные отношения и их свойства
Примеры
1. Перечислить и указать на координатной плоскости все элементы декартова произведения множеств А={-2, 1, 3} и В={-1, 0, 2, 5}.
Решение: А´В={(-2,-1), (-2,0), (-2,2), (-2,5), (1,-1), (1,0), (1,2), (1,5), (3,-1), (3,0), (3,2), (3,5)}.
|
2. 
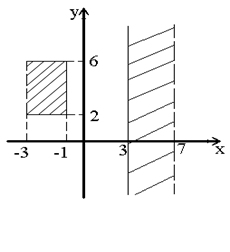Записать с помощью декартова произведения некоторых множеств фигуры, изображенные на рисунке:
Решение:
1) А´В, где А=(-3, -1], В=[2,6];
2) С´D, где С=[3, 7), D=(-¥, +¥).
3. Выяснить, какими свойствами обладает бинарное отношение h - «отношение больше» на множестве N.
Решение: Для любых натуральных чисел х hу, если х>у.
1) х>х – неверно для всех хÎN, т.е. данное отношение не является рефлексивным;
2) для всякой пары натуральных чисел из х>у не следует у>х, т.е. БО не является симметричным;
3) для любых х,уÎN выполняется одно из неравенств: х>у или у>х, т.е. отношение антисимметрично;
4) если х>у, а у>z, то справедливо х>z, т.е. БО транзитивно.
Задачи для самостоятельной работы
1. Записать множества А и В, если известно, что А´В={(3;1), (-3;4),
(0; 2), (1;3), (0;1), (5;7), (0;0), (5;5)}. Найти АÇВ, В\А. Изобразить на координатной прямой элементы множества В´А. Сколько элементов содержится в каждом из рассмотренных множеств?
2. На каком множестве задано БОg ={(2;3), (3;5), (5;7)}. Что можно сказать о его свойствах?
3. Выберите некоторое множество, задайте на нем БО, постройте для этого отношения ориентированный граф, по графу определите свойства БО.
4. 
Определить свойства следующих бинарных отношений:
1) r - «родство по крови»;
2) s - «быть знакомым»;
3) отношение «=» - равенства на множестве R (а также ¹, ³, <).
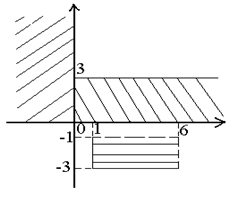
5. Записать с помощью декартова произведения множества точек координатной плоскости, указанные на рис. 20.
6. Постройте граф отношения, обладающего указанными ниже свойствами:
а) рефлексивность и транзитивность;
б) антисимметричность;
в) рефлексивность, симметричность и транзитивность.
7. Какие отношения эквивалентности можно задать на множестве N (R)? Какими еще свойствами они обладают? Изобразить на координатной плоскости прямое произведение N´R.
