Наиболее распространенными характеристиками совокупности являются:
1) среднее арифметическое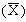 
2) среднее квадратическое (или стандартное) отклонение 
;
3) стандартная ошибка среднего арифметического 
;
4) коэффициент вариации (V).
1. Средним арифметическим называется частное от деления суммы всех значений вариант рассматриваемой совокупности на их число (n):
Среднее арифметическое обладает следующими свойствами:
а) измеряется в тех же единицах, что и основные варианты;
б) если каждое число совокупности уменьшить (увеличить) на одно и то же число, то ее среднее уменьшится (увеличится) на это же число;
в) если каждое число совокупности увеличить (уменьшить) в несколько раз, то ее среднее увеличится (уменьшится) в такое же число раз;
г) сумма отклонений статистических данных совокупности от их точного среднего всегда равна нулю:
(2)
2. Среднее квадратическое (или стандартное) отклонение 
.
Основной мерой статистического измерения изменчивости признака у членов совокупности служит среднее квадратическое отклонение (сигма) или, как часто ее называют, стандартное отклонение. Теория вариационной статистики показала, что для характеристики любой генеральной совокупности, имеющей нормальный тип распределения достаточно знать два параметра: среднюю арифметическую и среднее квадратическое отклонение. Эти параметры заранее не известны и их оценивают с помощью выборочной средней арифметической и выборочного стандартного отклонения, которые вычисляются при обработке случайной выборки.
В основе среднего квадратического отклонения лежит сопоставление каждой варианты 
со средней арифметической данной совокупности. Так как в совокупности всегда будут варианты как меньше, так и больше, чем она, то сумма отклонений 
), имеющих знак " - ", будет погашаться суммой отклонений, имеющих знак 
Отклонение вариант от своей средней арифметической выражает изменчивость признака. Если бы изменчивость признака у членов совокупности отсутствовала, тогда разность 
Но т.к.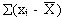 
всегда равна нулю, то для измерения изменчивости берут отклонение в квадрате, т.е. 
Если просуммировать квадраты отклонений, то эта сумма не будет равна нулю. А чтобы получить коэффициент, способный измерить изменчивость, берут среднее отклонение из выражения:
Величина 
называется девиатой (или взвешенной дисперсией), вариансой (или средним квадратом). Тогда среднее квадратическое отклонение имеет следующую формулу:
Свойства среднего квадратического (стандартного) отклонения:
1. Стандартное отклонение всегда измеряется в тех же единицах измерения, что и основные варианты.
2. Чем больше , тем больше изменчивость признака.
3. В вариационных рядах с нормальным распределением частот 99,7% всех членов совокупности находящихся в границах от 
, которые отстоят от средней арифметической на величину от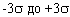 
. За пределами 
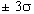находятся только 0,3% всех членов совокупности.
4. При вычислении стандартное отклонение определяют с точностью на один десятичный знак больше, чем точность, которую применяют для вычисления средней арифметической для того же ряда.
3. Стандартная ошибка средней арифметической или ошибка репрезентативности характеризует колебания средней. При этом необходимо отметить, что чем больше объем выборки, тем меньше разброс средних величин.
Стандартная ошибка средней вычисляется по формуле:
(5)
В современной научной литературе средняя арифметическая представляется вместе с ошибкой репрезентативности:
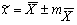. (6)
4. Коэффициент вариации (V). Изложенные выше характеристики совокупности (средняя арифметическая и среднее квадратическое отклонение) имеют один недостаток: они дают показатель изменчивости признака в именованных величинах, а не в относительных. Поэтому сопоставление (или сравнение) разноименных признаков по этим параметрам невозможно.
В этом случае удобно пользоваться коэффициентом изменчивости признака, который выражается в относительных величинах, а именно в процентах, и вычисляется по формуле:
, (7)
Чем больше V, тем более изменчив признак. Значения коэффициента вариации, невыходящие за пределы 10%, принято считать нормальными.
Если V>20%, то выборка некомпактна по заданному признаку.
Пример.
Определить основные статистические показатели результатов прыжка в длину группы спортсменов, если данные выборки таковы:
xi, см ~ 185, 171, 190, 170, 190, 178, 188, 174, 193, 178, 176, 180, 175, 176, 180, 192 (n=16).
Решение:
1. Для вычисления основных статистических показателей составим рабочую таблицу следующего вида:
|
| 
|
|
| 
| 
|
| 
| 
|
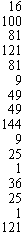
2. Для определения среднего арифметического используем формулу:
3. Для вычисления среднего квадратического отклонения определяем разности и заносим во 2 столбец. Находим квадраты этих разностей, записываем их в 3-ий столбец и рассчитываем 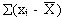Тогда:
4. Определить стандартную ошибку среднего арифметического, используя формулу:
5. Определим ошибку репрезентативности по формуле:
6. Определим коэффициент вариации по формуле:
Выводы: 1) среднее значение высоты прыжка составляет 181 см;
2) по показателю высоты прыжка группа компактна, т.к. стандартное отклонение составляет ± 7, 6 см, а коэффициент вариации — 4, 2 % (менее 10%).
