Программно найти самую левую на интервале [–2, 2] (с точностью 0,1) точку, в которой значение функции принимает отрицательное значение, и самую правую точку на том же интервале, в которой значение функции принимает положительное значение.
Пример выполнения задания 1
Вычислить значение выражения
 (1)
(1)
В переменной x хранятся входные данные, в переменной y — результат вычисления выражения.
Для вычисления выражения сначала необходимо вычислить cos(x), затем cos(2 x), и т. д., в последнюю очередь — cos(99 x).
Выражение (1) можно записать в виде последовательности однотипных рекуррентных выражений
 ;
;  ;
;  ;….;
;….;
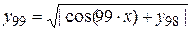
В общем, виде можно записать
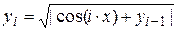 , где
, где  ;
; 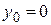 .
.
В связи с этим организуем цикл For с изменением счетчика от 1 до 99 с шагом 1.
Пример реализации программы
Private Sub Command1_Click()
Dim x As Double ' для хранения исходных данных
x = 0.01
Dim i As Byte ' счетчик цикла
Dim y As Double ' результат вычислений
y = 0
For i = 1 To 99
y = Sqr(Abs(Sin(i * x) + y))
Next i
Print y
End Sub
Пример выполнения задания 2
Вычисление значения функции, заданной графически, целесообразно оформить в виде функции f, аргументом которой является значение оси абсцисс.
Пример реализации программы
Function f(x As Double) As Double
Const R = 2
Select Case x
Case Is < – R
f = x + R
Case -R To R
f = Sqr(R ^ 2 – x ^ 2)
Case Is > R
f = 2
End Select
End Function
Private Sub Command1_Click()
Dim x As Double ‘ значение аргумента функции
Dim y As Double ‘ результат
Dim found As Boolean ‘ признак нахождения отрицат. значения функции
For x = –3 To 3 Step 0.2
y = f(x)
Print Round(x, 2), Round(y, 5) ‘вывод значения x, округленного до двух
‘знаков после десятичной точки и y — округленного до пяти знаков
Next x
found = False
For x = –2 To 2 Step 0.1
y=f(x)
If y < 0 Then
found = True
Print "Самая левая точка с отриц. значением функции ", Round (x, 1), y
Exit For
End If
Next x
If Not found Then Print "Нет точки с отрицательным значением функции"
End Sub
Контрольные вопросы
1. Оператор цикла For и его разновидности.
2. Понятие рекуррентной формулы.
3. Логический тип. Операции над величинами логического типа.
4. Функция округления.
Лабораторная работа 4
ОПЕРАТОРЫ ЦИКЛА С ПРЕД- И ПОСТУСЛОВИЕМ
Цель работы: Изучить операторы цикла c пред- и постусловием.
Краткие теоретические сведения
Цикл с условием Do … Loop в отличие от цикла с параметром For используется в тех случаях, когда число выполнения тела цикла заранее не известно, но определено условие выхода из цикла.
В зависимости от местоположения условия относительно тела цикла различают два варианта конструкции Do… Loop:
- цикл с предусловием:
Do While|Until < условие >
< операторы >
[Exit Do]
[< операторы >]
Loop
- цикл с постусловием:
Do
< операторы >
[Exit Do]
[< операторы >]
Loop While | Until < условие >
Графические способы изображения циклов с ключевым словом While приведены на рис. 5.
Аргумент условие конструкции является логическим выражением. Если оно равно True, то тело цикла Do … Loop While выполнится, если равно False, то происходит выход из цикла и управление передается конструкции следующей за Loop.






