При проектировании триангуляции существенную роль играет предвычисление точностей отдельных ее элементов и их оценка.
Под оценкой точности понимают подсчет ожидаемых средних квадратических ошибок различных элементов проектируемых и фактически полученных ошибок для построенных геодезических сетей.
Оценка точности триангуляции выполняется по весам соответствующих элементов триангуляции. Под весом в общем случае подразумевается величина, обратно пропорциональная квадрату средней квадратической ошибки, т.е.
, (8)
где С – постоянная величина.
Для оценки точности триангуляции рекомендуется использовать формулу средней квадратической ожидаемой ошибки логарифма связующей стороны ряда, удаленной от выходной стороны на n треугольников:
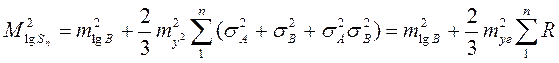(9)
где σ2А и σ2В - перемены логарифмов синусов связующих углов А и В при изменении их на одну секунду,
- средняя квадратическая ошибка измерения угла.
Величину 
называют ошибками геометрической связи треугольников.
Ошибка логарифма стороны, как весовое среднее из двух определений, без учета ошибок выходных сторон, определяется формулой:
(10)
где: МRI – ошибка слабой стороны, вычисленная от базиса В1;
МRII – ошибка слабой стороны, вычисленная от базиса В2.
Для перевода величины, выраженной в единицах логарифмов, в значения натуральных чисел надо величину МlgSR разделить на 0,43429 - модуль десятичных логарифмов или умножить на 2,3. Полученное значение выражают в относительной мере, т. е. определяют относительную ошибку 
.
Относительная ошибка искомой стороны будет:
, (11)
где М=lge=0,43429 или 1/М=2,3.
Среднюю квадратическую ожидаемую ошибку определения дирекционного угла связующей стороны с номером n можно вычислить по формуле:
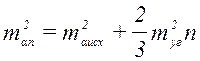(12)
где mα исх – ошибка дирекционного угла исходной стороны;
n – число связующих сторон.
Рассмотрим оценку точности запроектированной сети на рисунке 3.
На основе выше указанных требований запроектирована сеть триангуляции 4 класса, состоящая из шести треугольников. Наименьший угол между направлениями 4 класса равен 380. Все пункты располагаются на господствующих высотах местности для обеспечения видимости. Основные характеристики ряда: величины углов, величины R для каждого треугольника представлены в таблице 4. Величина R выбирается по двум связующим углам в треугольнике из приложения А.
Таблица 4
| № фигуры | Вид фигуры | Связующие углы | R |
| Исходная сторона b1 | |||
| треугольник -//-//- -//-//- | 68; 74 67; 68 65; 66 | 1,3 2,2 2,3 | |
| Исходная сторона b2 | |||
| треугольник -//-//- -//-//- | 48; 85 64; 75 38; 90 | 3,8 7,2 |
b1
I I II
680
670
740
III
650
680
IV
850 660
V
480 750
VI
380
640
VII
900 b2
VIII
Рисунок 3
Суммарная средняя квадратическая ожидаемая ошибка геометрической связи определения длины стороны IV – V, без учета ошибки выходной стороны b1, при mуг=2'' по формуле (9), будет
или 
Относительно стороны b2 получим
или 
Ошибка логарифма стороны IV – V, как весовое среднее из двух определений, без учета ошибок выходных сторон по формуле (10) будет равна
или
единицы шестого знака логарифма.
Для перевода величины, выраженной в единицах логарифмов, в значения натуральных чисел величину 
делим на 0,43429 – модуль десятичных логарифмов. Тогда mS IV-V =7,94 единицы шестого знака после запятой натуральных чисел или mS IV-V =0,00000794
Ожидаемая относительная ошибка слабой стороны будет
Вывод: Запроектированная сеть триангуляции 4 класса удовлетворяет требованиям инструкции.
