Рыночное равновесие меняется под воздействием неценовых факторов, к внерыночным из них относятся введение потоварных налогов и субсидий со стороны государства. В случае такого вмешательства в рыночное ценообразование происходит отклонение цен от их равновесных величин, а также изменение рыночных излишков сторон в зависимости от эластичности спроса и предложения.
Характер смещения кривых зависит не только от величины налога (субсидии), но и от способа взимания налога или предоставления субсидии. Так, налог (субсидия) могут быть как фиксированными (сумма на единицу товара), так и пропорциональными (по отношению к цене товара).
Если функции спроса и предложения заданы в виде QD = a – b∙P и QS = c + d∙P, то введение потоварных налогов и субсидий изменит эти функции следующим образом:
QD = a – b∙(P + T) = a – b∙(1 + t)∙P – введение потоварного налога на покупателей (потребителей) в сумме T (по ставке t);
QD = a – b∙(P – F) = a – b∙(1 – f)∙P – введение потоварной субсидии покупателям (потребителям) в сумме F (по ставке f);
QS = c + d∙(P – T) = c + d∙(1 – t)∙P – введение потоварного налога на продавцов (производителей) в сумме T (по ставке t);
QS = c + d∙(P + F) = c + d∙(1 + f)∙P – введение потоварной субсидии продавцам (производителям) в сумме F (по ставке f).
При прочих равных условиях налогообложение покупателей приводит к снижению и равновесной цены, и равновесного объёма, а их субсидирование – к увеличению и равновесной цены, и равновесного объёма.
При прочих равных условиях налогообложение продавцов приводит к увеличению равновесной цены и снижению равновесного объёма, а их субсидирование – к снижению равновесной цены и увеличению равновесного объёма.
Сумма налоговой нагрузки (TΣ) определяется по формуле:
|
TΣ = (PD – PS)∙Q1,
где PD – цена спроса при равновесном объёме Q1;
PS – цена предложения при равновесном объёме Q1;
Q1 – равновесный объём после налогообложения.
Несмотря на то, что плательщиком налога (получателем субсидии) могут быть определена одна из сторон, экономического распределение налоговой нагрузки (выгоды от субсидии) имеет место в отношении обеих сторон.
Если спрос неэластичный относительно предложения, бóльшую часть налоговой нагрузки будут нести покупатели, а меньшую – продавцы (и наоборот).
Части налоговой нарузки, приходящиеся на покупателей (TD) и продавцов (TS), могут быть определены как графически (см. пример 1 для задания 2), так и аналитически.
|
где PD – цена спроса при равновесном объёме Q1;
P0 – равновесная цена до налогообложения;
PS – цена предложения при равновесном объёме Q1;
Q1 – равновесный объём после налогообложения.
Чистые потери рыночных излишков сторон после налогообложения (DWL) определяются по формуле:
|
DWL = (PD – PS)∙(Q0 – Q1)/2,
где PD – цена спроса при равновесном объёме Q1;
PS – цена предложения при равновесном объёме Q1;
Q0 – равновесный объём до налогообложения;
Q1 – равновесный объём после налогообложения.
Выгода от предоставления субсидии покупателям (BD) и продавцам (BS) определяется как графически (см. пример 2 для задания 2), так и аналитически:
|
где P0 – равновесная цена до налогообложения;
PD – цена спроса при равновесном объёме Q1;
Q1 – равновесный объём после субсидирования;
PS – цена предложения при равновесном объёме Q1.
Графически площади прямоугольников, которые соответствуют долям выгоды от субсидии покупателям и продавцам, «меняются местами» в сравнении с соответствующими долями налоговой нагрузки, так как в случае налогообложения PD > PS при равновесном объёме, а в случае субсидирования, наоборот, PS > PD при равновесном объёме.
Распределение выгод от субсидии, как и распределение налогового бремени, определяется относительной эластичностью спроса и предложения. Если спрос неэластичный относительно предложения, бóльшую часть выгоду от субсидии будут получать покупатели, а меньшую – продавцы (и наоборот).
Примеры решения типовых задач
Задание 1
Применение методов Слуцкого и Хикса основано на следующих расчётах. Пусть I = 18, PX = 9, PY = 3, ΔI = +9, ΔРХ = -3. Выполнение заданий Б и В представлено на рис. 1 (в отличие от условия задания их выполнение показано последовательно, т. е. после ΔI следует ΔРХ).
|
|
|
|
|

Рисунок 1 – Применение метода Слуцкого для расчёта эффектов замены и дохода
Начальная бюджетная линия B1 при I = 18 имеет крайние точки:
Хmax = I/PX = 18/9 = 2, Ymax = I/PY = 18/3 = 6.
Координаты точки Е1: X = 1, Y = 3 (результат решения системы уравнений (4) задачи максимизации полезности).
Новая бюджетная линия B2 при I = 27 (ΔI = +9) имеет крайние точки:
Хmax = 27/9 = 3, Ymax = 27/3 = 9 (соотношение цен не изменилось).
Координаты точки Е2: X = 1,5, Y = 4,5 (результат решения системы уравнений задачи максимизации полезности).
Новая бюджетная линия B3 при РХ = 6 (ΔРХ = -3) имеет крайние точки:
Хmax = 27/6 = 4,5, Ymax = 27/3 = 9 (соотношение цен изменилось).
Координаты точки Е3: X = 2,25, Y = 4,5 (результат решения системы уравнений задачи максимизации полезности).
Общий эффект изменения потребления товара Х (переход от Е2 к Е3):
2,25 – 1,5 = 0,75 ед.
Он делится на эффект замены и эффект дохода, которые определяются по методу Слуцкого и методу Хикса, приводящим к разным результатам.
Определим эффект замены по Слуцкому – при условии сохранения структуры набора товаров (Е2), то есть по методу эквивалентов (восстановление исходной покупательной способности). Для этого нужно построить условную бюджетную линию (отмечена крупным пунктиром) через точку Е2 при PХ = 6, PY = 3:
I’ = 6∙1,5 + 3∙4,5 = 22,5.
Этот доход позволяет приобрести набор товаров Е2 при указанном снижении цены товара Х. Крайние точки этой бюджетной линии: Хmax = 3,75, Ymax = 7,5.
Разность исходного дохода и условного дохода представляет собой эквивалентную вариацию дохода (EV): 27 – 22,5 = 4,5. Это означает, что бюджет потребителя можно снизить на эту величину для сохранения структуры набора товаров.
Решаем систему уравнений для нахождения координат условной точки Е’, позволяющей графически выделить эффекты замены и дохода:




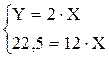


Это – координаты точки E’.
Эффект замены – это переход от точки Е2 к точке E’, эффект дохода – переход от точки E’ к точке Е3:
- эффект замены – 1,875 – 1,5 = 0,375 ед.
- эффект дохода – 2,25 – 1,875 = 0,375 ед.
Одинаковые величины эффектов для товара Х связаны с «симметричностью» функции полезности.
Другой способ определения эффект замены – по Хиксу – при условии сохранения исходной величины полезности, то есть по методу компенсаций (восстановление исходного уровня полезности, т. е. благосостояния). Для этого нужно построить условную бюджетную линию (отмечена крупным пунктиром на рис. 2) по касательной к кривой безразличия U2 при ценах PХ = 6, PY = 3:
Уровень полезности в точке Е2 равен:
 .
.
Определяем величину дохода для этой полезности при ценах PХ = 6, PY = 3:
 => M’ ≈ 22.
=> M’ ≈ 22.
Этот доход позволяет приобрести другой набор товаров (не Е2) при указанном снижении цены товара Х и сохранении полезности U2. Крайние точки этой бюджетной линии: Хmax = 22/6 ≈ 3,7, Ymax = 22/3 ≈ 7,3.
Разность исходного дохода и условного дохода представляет собой компенсирующую вариацию дохода (EV): 27 – 22 = 5. Это означает, что бюджет потребителя можно снизить на эту величину для сохранения исходной величины полезности.
|
|
|
|
|

Рисунок 2 – Применение метода Хикса для определения эффектов замены и дохода
Далее решаем систему уравнений:

Находим Х и Y (координаты точки E’) и выделяем эффекты замены и дохода аналогично графику выше. Величины этих эффектов будут не равны соответствующим эффектам по Слуцкому.
Пример построения графиков некомпенсированного спроса (по Маршаллу) и компенсированного спроса (по Хиксу) приведен на рис. 3рисунке 2ния эффектов замены и доходая:, так и ть определены аналитически.
абьотаетагрузки будут нести покупатели, а меньшую. Точка А – исходное равновесие, точка В – новое равновесие после увеличения цены товара Х, точка С – новое равновесие после построение компенсирующей – пунктирной – бюджетной линии по Хиксу.
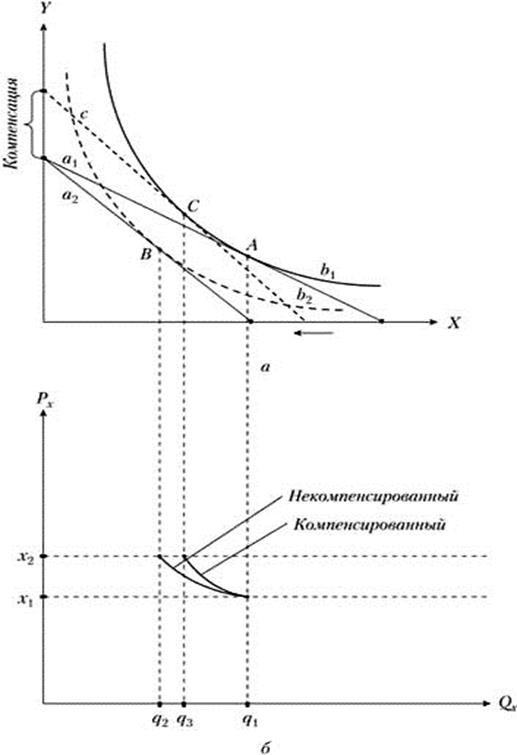
Рисунок 3 – Построение графиков некомпенсированного (маршаллианского)
и компенсированного (хиксианского) спросарисунке 2ния эффектов замены и доходая:, так и ть определены аналитически.
абьотаетагрузки будут нести покупатели, а меньшую
Задание 2
Пример 1
Определим особенности применения потоварного налога на продавца. Пусть функция спроса на товар QD = 7 – P, Функция предложения товара QS = -5 + 2∙Р, где QD и QS – объёмы спроса и объём предложения в млн. шт. в год, Р – цена в руб. На товар введен налог, уплачиваемый продавцом в размере 1,5 руб. за единицу.
1. Определяем равновесную цену и равновесный объём продаж
При равновесии QD = QS: 7 – Р = -5 + 2∙Р
РE = 4 руб. (равновесная цена)
QD = 7 – 4 = 3, QS = -5 + 2∙4 = 3,
QE1 = 3 млн. шт. (равновесный объём).
2. Определяем параметры нового равновесия после введения налога
При введении налога на продавца равновесные цены покупателя РD и продавца РS составят:
РD = РS – 1,5.
Фунции спроса и предложения, соответственно, имеют вид:
QD = 7 – Р и QS = -5+2∙(Р – 1,5)
Следовательно, 7 – Р = -5 + 2∙(Р – 1,5)
Отсюда РD = 5 руб., РS = 3,5 руб., QE2 = 2 млн. шт.
Таким образом, при налогообложении кривая предложения сдвигается влево на величину налога по вертикали (если он задана в абсолютном, а не в относительном выражении). Если он задана относительно, угол наклона кривой предложения изменяется и данное правило не работает.
3. Определяем излишки продавцов и покупателей до и после введения налога, величину налогового бремени, величину чистых общественных потерь от налогообложения.
Для ответа на эти вопросы воспользуемся графиком:

|
Рисунок 4 – Изменение рыночного равновесия при налогообложении продавцов
До введения налога излишек продавцов – это площадь ΔСРеВ, а излишек покупателей – это площадь ΔАРеВ. Таким образом:
- излишек продавцов: (4 – 2,5)∙3/2 = 2,25 млн. руб.
- излишек покупателей: (7 – 4)∙3/2 = 4,5 млн. руб.
После введения налога излишек продавцов– это площадь ΔСРSМ, а излишек покупателей – это площадь ΔАРDL. Таким образом:
- излишек продавцов: (3,5 – 2,5)∙2/2 = 1 млн. руб.
- излишек покупателей: (7 – 5)∙2/2 = 2 млн. руб.
Сумма налогового бремени определяется площадью прямоугольника РDLМРS, что составляет (PD – PS)∙QE2 = (5 – 3,5)∙2 = 3 млн. руб.
Налоговое бремя распределяется следующим образом:
- на покупателей: (PD – PE)∙QE2 = (5 – 4)∙2 = 2 млн. руб.
- на продавцов: (PE – PS)∙QE2 = (4 – 3,5)∙2 = 1 млн. руб.
Распределение зависит от угла наклона функций спроса и предложения.
Чистые общественные потери от введения налога – это площадь ΔLBM:
(PD – PS)∙(QE1 – QE2)/2 = (5 – 3,5)∙(3 – 2)/2 = 0,75 млн. руб.
Пример 2
Определим особенностиприменения потоварной субсидии на продавца. Пусть функция спроса имеет вид: QD =500 – P, функция предложения: QS = 2∙P – 100.Производителям товара представляется субсидия в размере 75 руб. за единицу товара.
1. Определяем равновесную цену и равновесный объём продаж:
500 – Р = 2∙Р – 100
РE = 200 руб., QE =300 шт. – параметры начального равновесия в точке E0.
2. Определяем параметры нового равновесия после субсидирования, общую величину субсидии и её распределение.
1-й способ – корректировка уравнения предложения:
500 – P = -100 + 2∙(P + 75)
РE = 150 руб., QE =350 шт. – параметры нового равновесия в точке E1.

Рисунок 5 – Изменение рыночного равновесия при субсидировании продавцов
Таким образом, при субсидировании кривая предложения сдвигается вправо на величину субсидии по вертикали (если она задана в абсолютном, а не в относительном выражении). Если она задана относительно, угол наклона кривой предложения изменяется и данное правило не работает.
2-й способ – корректировка уравнения спроса, который наглядно позволяет представить «разрыв» между ценами предложения и спроса при субсидировании продавца:
500 – PD = -100 + 2∙PS
500 – (PS – 75) = -100 + 2∙PS
РS = 225 руб., QE =350 шт., PD= 225 – 75 = 150 руб.
Общая сумма субсидии равна: 350∙75 = 26250 руб.
Распределение величины субсидии:
- на покупателя: (200 – 150)∙350 = 17500 руб.
- на продавца: (225 – 200)∙350 = 8750 руб.
Всего: 17500 + 8750 = 26250 руб.
Рекомендуемая дитература: [1] c.9-80, [2] c.111-265, [3] c.69-111
Вопросы для самоконтроля
1. Потребительский выбор и принципы рационального поведения. Свойства предпочтений (выпуклость, монотонность, локальная ненасыщаемость, гомотетичность)
2. Функция полезности как отражение предпочтений. Бюджетное ограничение. Множитель Лагранжа. Теорема Эджуорта
3. Эффекты дохода и замещения (по Слуцкому и Хиксу): графическая и аналитическая интерпретация. Теорема полезности Хикса
4. Первоначальная наделенность благами. Учет первоначальной наделенности благами
5. Бюджетное ограничение, включающее предварительный набор
6. Уравнение Слуцкого. Уравнение Слуцкого с учетом первоначального запаса
7. Задача восстановления предпочтений (integrability problem). Восстановление предпочтений по функции расходов
8. Измерение изменений в благосостоянии потребителя: компенсирующая вариация, эквивалентная вариация и потребительский излишек
9. Излишек потребителя. Анализ потребительского излишка по Маршаллу и Хиксу
10. Проблема агрегирования спроса. Потребительский спрос: индивидуальный и рыночный. Внешние эффекты в потреблении. Дополнения М. Алле
11. Проблемы теории ожидаемой полезности: парадокс Алле, эффекты контекста или рамочные эффекты, точка отсчета
12. Свойства функций спроса и косвенной функции полезности. Тождество Роя
13. Соотношения между спросом, косвенной функцией полезности и функцией потребительских расходов
14. Свойства функций спроса и функции расходов. Лемма Шепарда
15. Агрегированная функция спроса по группе потребителей и по группе благ
16. Выявленные предпочтения. Слабая аксиома о выявленных предпочтениях
17. Сильная аксиома о выявленных предпочтениях
18. Временные предпочтения. Предельная норма временного замещения. Межвременный выбор
19. Спрос потребителя в неопределенности. Функция ожидаемой полезности
20. Способы описания технологий: производственное множество, производственная функция и множество необходимых факторов производства.
21. Типы производственных функций: возможность выбора технологии. Свойства производственных множеств
22. Математические свойства производственных функций, их экономическая интерпретация
23. Задача максимизация прибыли и свойства функции прибыли
24. Задача минимизация издержек и свойства функции издержек
25. Максимизация и оптимизация прибыли. Изоклинали и изопрофиты
26. Уравнение Слуцкого в теории производства. Восстановление производственной функции исходя из спроса на факторы производства. Агрегирование в производстве
27. Влияние изменения цены продукции и цен ресурсов на объем спроса на ресурсы
28. Воздействие налогов, субсидий, внешнего рынка на рыночное равновесие
29. Теория неопределенности в экономике
30. Теория экономического риска Ф. Найта
31. Отношение субъекта к риску (антипатия, нейтральность, предпочтение)
32. Премия за риск. Безрисковый эквивалент лотереи
33. Измерение антипатии к риску, коэффициент Эрроу-Пратта: абсолютный и относительный
34. Инвестирование в рисковые активы. Теорема Самуэльсона о диверсификации
35. Модель Марковица. Множество эффективных портфелей
36. Оптимальные контракты для рискофоба и рисконейтрала при ненаблюдаемых усилиях.
37. Универсальные методы предупреждения и снижения риска.
38. Внешние эффекты. Внешние эффекты в производстве и потреблении
39. Внешние эффекты, создаваемые общественными благами
40. Равновесие в условиях внешних эффектов. Интернализация внешних эффектов.
41. Общественные блага: неделимость и неисключаемость
42. Оптимальный объем производства общественных благ
43. Особенности индивидуального и рыночного спроса на общественные блага
44. Стимулирование достоверности информации о спросе на общественное благо
45. Общественный выбор по Дж. Бьюкенену. Теорема невозможности К. Эрроу
46. Функция общественного благосостояния
47. Модели «линейного» города (Хотеллинг) и «кругового» города (Сэлоп).
48. Рынки с ассиметричной информацией
49. Влияние ассиметричной информации на эффективность рыночного равновесия
50. Проблемы риска безответственности контрагента и неблагоприятного отбора
51. Модель информационного взаимодействия «заказчик-исполнитель»
52. Стимулирующие контракты и эффективность
53. Влияние ассиметрии информации на отдельные рынки
54. Модели морального риска на рынке страхования и неблагоприятного отбора
Задания к работе
Задание 1. Моделирование поведения потребителя
Поведение потребителя исследуется на основе двухпродуктовой модели выбора товаров X и Y. Функция полезности имеет вид: U = (X∙Y)α.
А. Равновесие потребителя (рис. 1):
1. Вывести косвенную функцию полезности и рассчитать величину общей полезности, вывести уравнение кривой безразличия U1.
2. Построить бюджетную линию В1 на основе двух её крайних точек.
3. Определить графически и математически точку равновесия Е1.
4. Определить величину предельной нормы замещения (MRS) в точке E1.
Б. Изменение равновесия потребителя при изменении дохода (рис. 2):
1. Построить кривую безразличия U1 и бюджетную линию В1.
2. Рассчитать величину общей полезности после изменения дохода, вывести уравнение кривой безразличия U2.
3. Построить бюджетную линию В2 на основе двух её крайних точек.
4. Определить графически и математически точку нового равновесия Е2.
5. Определить величину предельной нормы замещения (MRS) в точке E2.
6. Построить линию «доход – потребление» (ICC).
7. На основе рис. 2 построить график линий Энгеля (рис. 2а) и определить характер товаров X и Y (полноценные или неполноценные).
В. Изменение равновесия при изменении цены товара Х (рис. 3):
1. Построить кривую безразличия U1 и бюджетную линию В1.
2. Рассчитать величину общей полезности после изменения цены товара, вывести уравнение кривой безразличия U3.
3. Построить бюджетную линию В3 на основе двух её крайних точек.
4. Определить графически и математически точку нового равновесия Е3.
5. Определить величину предельной нормы замещения (MRS) в точке E3.
6. Построить линию «цена – потребление» (PCC).
7. Построить эквивалентную бюджетную линию по методу Слуцкого и рассчитать величину эквивалентной вариации дохода (EV).
8. Рассчитать количественно и показать графически величины эффекта замены, эффекта дохода и общего эффекта по Слуцкому.
9. Построить компенсирующую бюджетную линию по методу Хикса (рис. 3а) и рассчитать величину компенсирующей вариации дохода (СV).
10. Рассчитать количественно и показать графически величины эффекта замены, эффекта дохода и общего эффекта по Хиксу.
11. На основе линии РСС построить функцию индивидуального спроса на товар Х (спрос Маршалла), на основе компенсирующей вариации дохода построить функцию компенсированного спроса на товар Х (спрос Хикса) (рис. 3б).
Задание 2. Влияние налогов и дотаций на рыночное равновесие
Рыночный спрос представлен графиком индивидуального спроса на товар X (некомпенсированный спрос Маршалла, полученный в Задании 1 в п.В.11). График предложения товара Х построен из начала координат и пересекает линию спроса в точке первоначального равновесия потребителя Х(Е1).
Необходимая точность вычислений – до сотых (цена), до десятых (объём).
А. Рыночное равновесие (рис. 1):
1. Вывести функции спроса и предложения товара Х.
2. Построить график рыночного равновесия.
3. Определить величину прямой эластичности спроса и предложения в точке равновесия Е1.
Б. Влияние потоварного налога на спрос (рис. 2):
1. Определить изменение параметров рыночного равновесия при налогообложении покупателей в размере 20% от первоначальной равновесной цены.
2. Определить величину прямой эластичности спроса и предложения в точке нового равновесия Е2.
3. Определить изменение излишков продавцов и покупателей.
В. Влияние потоварной субсидии на спрос (рис. 3):
1. Определить изменение параметров рыночного равновесия при субсидировании покупателей в размере 20% от первоначальной равновесной цены.
2. Определить величину прямой эластичности спроса и предложения в точке нового равновесия Е3.
3. Определить изменение излишков продавцов и покупателей.
4. Найти распределение величины субсидирования между продавцами и покупателями.
В. Влияние потоварного налога на предложение (рис. 3):
1. Определить изменение параметров рыночного равновесия при налогообложении продавцов в размере 20% от первоначальной равновесной цены.
2. Определить изменение излишков продавцов и покупателей.
3. Найти распределение налоговой нагрузки между продавцами и покупателями.
4. Найти величину чистых общественных потерь от налогообложения.
Г. Влияние потоварного субсидирования на предложение (рис. 4):
1. Определить изменение параметров рыночного равновесия при субсидировании продавцов в размере 20% от первоначальной равновесной цены.
2. Определить изменение излишков продавцов и покупателей.
3. Найти распределение величины субсидирования между продавцами и покупателями.
Примечание: в отличие от задания 1, части Б-Д задания 2 можно выполнять в любом порядке.
Таблица выбора варианта заданий
Вариант выбирается по сумме трех последних цифр зачетной книжки.
Таблица 1 – Исходные данные по вариантам
| Вариант | Параметр α функции полезности | Доход (І) | Цена товара X (PX) | Цена товара Y (РY) | Изменение дохода (ΔІ) | Изменение цены товара X (ΔРХ) |
| 0,5 | +20 | + 10 | ||||
| -40 | +20 | |||||
| -20 | -10 | |||||
| 0,5 | +40 | +30 | ||||
| -40 | +30 | |||||
| +40 | +10 | |||||
| 0,5 | -80 | +60 | ||||
| -160 | +40 | |||||
| -30 | +20 | |||||
| 0,5 | -60 | +30 | ||||
| -60 | +40 | |||||
| +60 | +30 | |||||
| 0,5 | -60 | -10 | ||||
| +60 | -10 | |||||
| -60 | +10 | |||||
| 0,5 | +60 | -10 | ||||
| +40 | +10 | |||||
| -40 | +30 | |||||
| 0,5 | -100 | +40 | ||||
| +100 | +10 | |||||
| +70 | -10 | |||||
| 0,5 | +70 | -50 | ||||
| +70 | -50 | |||||
| -70 | +50 | |||||
| 0,5 | -60 | +20 | ||||
| +40 | -2,5 | |||||
| -130 | +20 | |||||
| 0,5 | +130 | -25 |
Образец оформления титульного листа






