I. Основные теоретические положения о теплообмене
при пленочной конденсации
При работе паровых энергетических и холодильных установок, в аппаратах кондиционирования воздуха и системах терморегулирования космических кораблей и т.п. постоянный уровень температуры для отвода или подвода теплоты часто достигается при конденсации паров рабочего тела – воды, фреонов, металлических, органических и других теплоносителей. Процесс конденсации занимает также важное место в химико-технологических производствах, например, в нефтехимии.
Движущей силой рассматриваемого процесса является разность парциальных давлений паров конденсирующейся жидкости над теплообменной поверхностью и на достаточном удалении от нее. Последнее достигается охлаждением упомянутой поверхности до температуры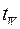 
более низкой, чем температура насыщения паров 
, находящихся в объеме теплообменного аппарата, называемого конденсатором. Заметим сразу, что теплообменные поверхности в конденсаторах составляются из размещенных внутри цилиндрического кожуха труб или пластинчатых каналов, внутри которых движется охлаждающая среда – воздух, вода и т.д.
При отсутствии жировых или масляных пятен конденсация паров на большинстве технических поверхностей происходит в каждой точке и называется пленочной. Процесс пленочной конденсации представляется как диффузия молекул паров из парового пространства к стекающей по охлаждаемой поверхности пленке конденсата с последующей отдачей теплоты фазового превращения через толщу пленки конденсата к охлаждаемой стенке.
При отсутствии в паровом объеме конденсатора примесей неконденсирующихся газов сопротивление диффузии паров к стекающей пленке конденсата пренебрежимо мало и термическое сопротивление процессу конденсации практически определяется теплофизическими свойствами и характером течения пленки (ламинарным, переходным или турбулентным), а также взаимодействием ее с поступающим в конденсатор паром, скорость которого может быть весьма значительной.
Задача об определении интенсивности теплообмена при пленочной конденсации была впервые решена В. Нуссельтом в 1916 г. Он рассматривал процесс конденсации неподвижного пара на вертикальной охлаждаемой пластине шириной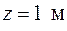 
(рис. 16.1) в упрощающих предпосылках о том, что пленка конденсата движется ламинарно, безынерционно и безградиентно.
Тогда процесс течения пленки таков, что гравитационная сила, действующая на выделенную часть пленки высотой dy уравновешивается силой трения ее о стенку, т.е.
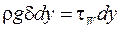, (16.1)
где ρ – плотность жидкости; g – ускорение свободного падения; δ – толщина плёнки;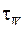 
- касательное напряжение трения на стенке.
 
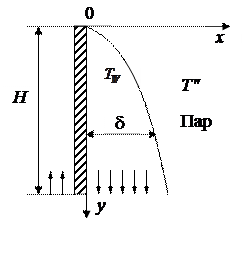Рис. 16.1. Схема процесса конденса-ции пара на вертикальной пластине
| Приращение dm массы стекающей жидкости на высоте пластины определяет движение пленки конденсата и обуслов-лено конденсацией пара на каждом выделенном элементе dy:
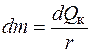 , (16.2)
где 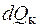 - количество теплоты, выделенное при конденсации; r – теплота фазового превращения.
|
С другой стороны, величина dm может быть определена дифференцированием выражения для массы конденсата m, проходящей через сечение, отстоящее на расстояние y от верхнего края пластины:
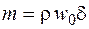. (16.3)
Неизвестная средняя скорость движения жидкости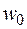 
в рассматриваемом сечении легко вычисляется при совместном рассмотрении системы уравнений, состоящей из динамического уравнения (16.1) и приводимых ниже уравнения (16.4) параболической формы профиля скоростей для ламинарного течения и уравнения (16.5) закона Ньютона для касательного напряжения трения :
, (
)
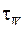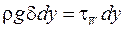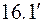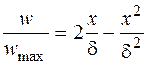, (16.4)
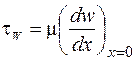. (16.5)
В самом деле, вычисляя 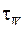через (16.1) как 
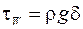и через (16.5) путем предварительного определения на стенке градиента скорости пленки 
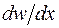дифференцированием уравнения профиля скоростей (16.4) в точке x = 0 как 
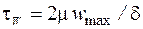, получаем тождество:
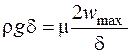или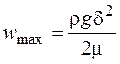 
. (16.6)
В уравнениях (16.4) и (16.5) дополнительно обозначены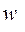 
– скорость жидкости в точке, отстоящей в рассматриваемом сечении на расстоянии x от стенки; 
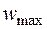- максимальное значение скорости в том же сечении; 
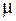– динамическая вязкость жидкости.
При параболическом профиле скоростей средняя скорость жидкости 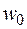составляет 2/3 от ее максимального значения
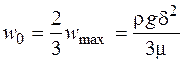(16.7)
и масса конденсата m, проходящего через рассматриваемое сечение, определяется как
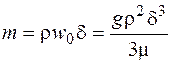, (16.8)
тогда приращение массы конденсата dm на высоте пластины dy равно:
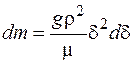. (16.9)
