При кипении воды в большом объеме

 

I. Основные теоретические положения о теплообмене

при пузырьковом кипении в большом объеме

 

Процесс кипения жидкости распространен в технике: он применяется для производства пара на предприятиях тепло- и электроэнергетики (ТЭЦ, ТЭС, ГРЭС, АЭС и др.), имеет место в холодильных установках при подводе теплоты на постоянном температурном уровне, в химико-технологических процессах разделения многокомпонентных жидкостей и др.

Кипение жидкости характеризуется большими значениями коэффициента теплообмена и практически никогда не лимитирует температурные условия работы теплообменной поверхности.

Различают две формы образования паровой фазы из жидкой:

1. Жидкость соприкасается с поверхностью, имеющей температуру более высокую, чем температура парообразования (кипения) . Такая поверхность является источником возмущения, приводящим к появлению второй фазы, так как процесс парообразования начинается на такой обогреваемой поверхности в существенно неравновесной форме.

2. Температура жидкости остается постоянной, но происходит резкий сброс давления, приводящий к внезапному бурному процессу неравновесного парообразования во всем объеме жидкости. Такой процесс типа взрыва очень опасен в системах с большим объемом жидкости при резком увеличении расхода пара.

Мы будем рассматривать только процесс парообразования на обогреваемой поверхности, который также подразделяется на два вида:

а) температура массы жидкости доведена до состояния насыщения , т.е. нормальное парообразование;

б) жидкость во всем объеме имеет температуру меньшую, чем температура насыщения, а поверхность теплообмена перегрета выше температуры парообразования, т.е. теплообмен при кипении происходит при недогретой жидкости. В иностранной литературе такую жидкость называют переохлажденной по отношению к состоянию насыщения при давлении в сосуде.

Изучим нормальную форму кипения и привлечем к рассмотрению термодинамические методы анализа фаз в момент возникновения новой (паровой) фазы в дисперсной форме (в форме пузырьков) у перегретой поверхности.

Известно, что в течение всего процесса кипения поддерживаются постоянными и находятся в соответствии друг с другом внешнее давление p и температура жидкости на достаточном удалении от теплообменной поверхности. В этих условиях сопряжения зародившегося пузырька пара и внешней среды в качестве характеристической функции нужно выбрать свободную энтальпию

 

, (15.1)

 

где F – свободная энергия; p – давление; V – сумма объемов всех фаз – жидкой , парообразной и разделяющего их поверхностного слоя в 2-3 молекулы толщиной , равная

 

.

 

Из-за малости объема им пренебрегаем. Заметим, кстати, что увеличение объема пара происходит за счет уменьшения объема жидкости .

В дифференциальном виде формула (15.1) запишется как

 

 

или

 

 

Применение индексов связано с тем, что ниоткуда не следует их идентичность во всех фазах. Термодинамический анализ поверхностной фазы показывает, что имеет место равенство

 

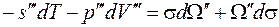, (15.2)

 

где s – коэффициент поверхностного натяжения, равный чаще всего – поверхность раздела фаз, определяемая объемом новой фазы (пара), а не жидкости.

Используя условия сопряжения p = const и T = const, получаем

 

.

 

Дифференциал свободной энтальпии d Ф в этом случае определится как

 

. (15.3)

 

В состоянии равновесия характеристическая функция – свободная энтальпия – имеет минимальное значение Ф_min и дифференциал этого экстремального значения равен нулю (d Ф_min=0):

 

. (15.4)

 

Преобразуем (15.4) к виду

 

, ()

 

в котором величины и независимы друг от друга и не равны нулю, следовательно, в () равны нулю коэффициенты при и , т.е. давление в жидкой фазе равно внешнему

 

или (15.5)

 

и

 

или . (15.6)

 

Отношение зависит от формы паровой фазы и чем сложнее форма, тем больше поверхность паровой фазы при одном и том же объеме . Минимальную поверхность при данном объеме имеет шар и для него верно соотношение:

 

. (15.7)

 

Тогда на основании (15.6) и (15.7) получаем, что давление в сферическом паровом пузырьке радиуса R равно

 

. (15.8)

 

Уравнение (15.8) другим путем получено математически Гауссом и на основании физических соображений Лапласом.

Итак, мы пришли к необычному соотношению – внутри пузырька и в окружающей среде температура одна и та же , а на самом деле это физически невозможно из-за наличия поверхностного натяжения, так как при не очень больших размерах пузырьков R давление жидкости не равно давлению пара и разница между ними согласно (15.8) достигает значительной величины.

Последнее возможно лишь в случае, если новая фаза (пар) образуется из жидкости с температурой большей на , чем температура насыщения , соответствующая внешнему давлению p. Давление пара такой жидкости больше внешнего давления p на величину , предотвращающую раздавливание пузырька силами поверхностного натяжения.

В слое парообразования жидкость должна быть перегрета еще на величину с тем, чтобы повысить давление в пузырьке на величину

 

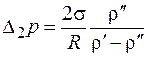(15.9)

 

( и - соответственно плотности жидкости и пара), так как поверхность пузырька вогнутая, а над вогнутой поверхностью давление ниже, чем над плоской на . Формула (15.9) была установлена Томсоном-Кельвином.

Итак, суммируя все вышеуказанное, получаем, что жидкость в слое образования пузырьков пара радиусом R должна быть перегрета по отношению к температуре насыщения на величину , и тогда давление пара в пузырьке становиться достаточным как для “сдерживания” раздавливающих сил поверхностного натяжения, так и для компенсации эффекта уменьшения давления над вогнутой поверхностью по сравнению с внешним давлением.

При этом пар в пузырьке находится при температуре, равной температуре насыщения меньшей, чем температура окружающей его жидкости , так как тепло должно переходить от жидкости к пару и необходим температурный напор (гипотеза Бошняковича).

Величину перегрева , необходимого для равновесного существования пузырька радиусом R, вычислим по уравнению Клапейрона-Клаузиуса, хотя оно и выведено для равновесных фазовых превращений над плоской поверхностью раздела жидкости и пара

 

, (15.10)

 

где r – теплота фазового превращения, Дж/кг; - термодина-мическая температура насыщения, К; и - удельные объемы пара и жидкости, м³/кг.

Переходя от дифференциалов к конечным разностям, получаем

 

, ()

 

где

 

. (15.11)

 

Для большинства технических жидкостей величина перегрева жидкости в слое пузырькового парообразования достигает °. Типичное распределение температуры над теплообменной поверхностью при пузырьковом кипении приведено на рис. 15.1.

Для каждой степени перегрева существует свой радиус пузырька, которому отвечает его равновесие с жидкостью, он называется критическим радиусом пузырька . Самозарождение пузырька невозможно, так как при 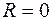из (15.11) получается, что , тогда на основании () имеем . Обязательно нужен начальный зародыш с конечным радиусом кривизны и жизнестойкость пузырька при заданном перегреве зависит от его радиуса: необходимо, чтобы радиус R зародыша был больше . Основными реальными центрами парообразования являются геометрические неровности поверхности нагрева, шероховатости, щели, бугорки, около которых образуются несмачиваемые впадины. Число зародышей становится тем больше, чем больше величина перегрева жидкости или разность температур стенки 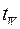и насыщения жидкости , которую также принято называть перегревом жидкости и использовать в качестве движущей силы
(в качестве температурного напора) при расчете интенсивности теплообмена при кипении.

 

 

Рис. 15.1. Типичное распределение температуры в жидкости

над теплообменной поверхностью

 

Равновесия между пузырьком и окружающей его жидкостью в действительности не имеется: пузырек растет, в него идет непрерывный процесс испарения жидкости и постепенно увеличивается подъемная сила пузырька, равная

 

. (15.12)

В момент, когда величина подъемной силы сравнивается с силой поверхностного натяжения, равной

 

, (15.13)

 

и определяется отрывной радиус пузырька с точностью до постоянного сомножителя:

 

. (15.14)

 

Отбрасывая в правой части формулы (15.14) цифровые значения, получаем формулу для определения характерного размера при кипении жидкости в виде

 

(15.15)

 

Оторвавшись от поверхности и поднявшись вверх, пузырек попадает в область жидкости с температурой насыщения . При подъеме пузырек быстро растет: он получает 10-20 % пара у поверхности и 80-90 % при подъеме вверх.

По механизму явления различаются две стадии процесса парообразования.

Первая стадия характеризуется малыми температурными напорами (для воды при атмосферном давлении ); имеется мало центров парообразования, частота отрыва пузырьков мала. Это усиленная поднимающимися пузырьками форма свободной конвекции жидкости над нагретой поверхностью (участок 0A на рис. 15.2).

Вторая стадия процесса кипения характеризуется большими температурными напорами (для воды при атмосферном давлении ) и соответствует области развитого пузырькового кипения (участок AB на рис. 15.2): отделение пузырьков становится более частым (через сотые доли секунды), в процессе участвует все большее число центров парообразования, жидкость буквально фонтанирует при выбросе пузырька и замещает его на пластине. Эффект турбулизации жидкости в пристеночной области делает весьма интенсивным теплообмен: коэффициент теплоотдачи (и плотность теплового потока) при кипении резко возрастает ( до 35·10⁸ Вт/(м²K)).

 

Рис. 15.2. График зависимости a от D t при кипении воды

в большом объеме

 

Экспериментальные данные при кипении в большом объеме при неизменном давлении показывают, что имеется связь между интенсивностью теплообмена и плотностью теплового потока в виде

 

, (15.16)

 

где k – постоянная, учитывающая теплофизические свойства кипящей жидкости и т.п.

Для первой стадии кипения установлено, что n = 0,26, а для второй – n =0,7. Заметим, что формулу (15.16) можно привести к виду, удобному для выявления влияния величины перегрева D t на интенсивность теплообмена при кипении жидкости на обогреваемой поверхности, учитывая, что . Тогда имеем последовательно , и

. ()

 

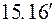Нетрудно видеть, что для второй стадии кипения, когда , рост коэффициента теплоотдачи с увеличением перегрева D t колоссален, так как он возрастает быстрее, чем по квадратичной зависимости:

 

. ().

 

При достижении некоторого значения плотности теплового потока, называемого критическим , число образующихся пузырьков столь велико, что они не успевают отводиться наверх и сливаются в сплошную паровую пелену, отделяющую жидкость от теплообменной поверхности (точка C на рис. 15.2). Такая форма процесса кипения называется пленочной, так как тепловой поток передается при этом механизмом теплопроводности от стенки через пелену перегретого пара к жидкости. Термическое сопротивление парового слоя очень велико (коэффициенты теплопроводности паров и газов весьма малы), коэффициент теплоотдачи резко уменьшается и обогреваемые стенки перегреваются. Пленочная форма кипения весьма опасна для теплообменных аппаратов, работающих под давлением.

Переход к пленочному кипению по линии ВС показан на рис.15.2 схематически. В действительности же этот переход протекает более сложно, т.к. существует переходный режим кипения, когда в одних и тех же местах на обогреваемой поверхности во времени чередуются развитое пузырьковое и пленочное кипение.

Реальные процессы перехода В ₁ С ₁ и В ₂ С ₂ отличаются способами увеличения количества подведенного тепла. В первом из них рост осуществляется при увеличении температуры греющей среды, например, при конденсации пара другой жидкости, имеющей более высокую температуру изменения агрегатного состояния, чем кипящей жидкости. В процессе же В ₂ С ₂ рост обеспечивается при электрическом и радиационном (лучистом) обогреве или в процессе распада ядерного топлива.

Отметим, что линия С ₃ В ₃ соответствует возврату от пленочного к пузырьковому кипению.

В заключение приведем также критериальную расчетную формулу для определения интенсивности теплообмена при пузырьковом кипении, предложенную академиком

 

(15.17)

где 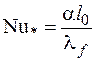- число Нуссельта; - критерий Рейнольдса при кипении, в котором фигурирует скорость парообразования и характерный размер и
Pr – коэффициент теплопроводности и критерий Прандтля для кипящей жидкости; - критерий, учитывающий влияние давления на теплообмен при кипении.

 

 

II. Описание опытной установки

Принципиальная схема опытной установки для изучения теплообмена при кипении жидкости в большом объеме приведена на рис. 15.3.

В сосуд 1 наливается до определенного уровня вода, медное днище сосуда 2 диаметром является теплообменной поверхностью, обогрев которой осуществляется электронагре-вателем 3. Мощность теплового потока регулируется автотрансформатором 4 и измеряется ваттметром 5. Процесс кипения визуально наблюдается в смотровые окна 6, уровень воды в сосуде контролируется по указателю уровня 7. Парогенератор снабжен сепаратором пара 8 и трубкой 9 возврата конденсата из конденсатора (на схеме не показан), поддерживающего давление в сосуде 1 на уровне атмосферного.

Температура поверхности измеряется тремя медно-константановыми термопарами 10, 11, 12, зачеканенными в днище 2, а температура кипящей воды - термопарой 13. Холодные концы термопар помещены в сосуд Дьюара 14 с тающим льдом, поддерживающий температуру 0°C. Показания термопар измеряются потенциометром 16, который сообщается с любой из них через переключатель 15.

 

 

Рис. 15.3. Принципиальная схема опытной установки для изучения