Количество энергии интегрального излучения Q, исходящего с поверхности излучающего тела в единицу времени, называется потоком излучения. Поток излучения тела, испускаемого единицей поверхности по всем направлениям полупространства (полусферы) называется плотностью полусферического излучения (Е вт/м2)
(7.4)
Поток излучения, исходящий со всей поверхности тела, равен
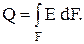(7.5)
Наиболее простыми и строгими законами описывается излучение абсолютно черного тела. Мы будем отмечать индексом «0» все параметры, относящиеся к абсолютно черному телу. Эти законы с соответствующими поправками используются для получения расчетных формул лучистого теплообмена между реальными телами.
Если обозначить через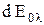 
– ту часть плотности излучения абсолютно черного тела, которая приходится на интервал длин волн от l до l+dl, то закон Планка для спектральной интенсивности излучения можно записать в виде
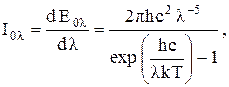(7.6)
где h=6,6252×10-34 дж×с – постоянная Планка;
k=1,38044×10-23 дж/0К – постоянная Больцмана;
с – скорость света;
l – длина волны;
Т – абсолютная температура черного тела. Зависимость спектральной интенсивности излучения абсолютно черного тела от длины волны при фиксированной температуре имеет максимум, отвечающий длине волны
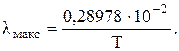(7.7)
Таким образом, максимум спектральной интенсивности излучения абсо-лютно черного тела с увеличением температуры перемещается в сторону более коротких длин волн. Это соотношение называют еще законом смещения Вина.
Абсолютно черное тело имеет сплошной спектр излучения, т. е. излучает все длины волн от l=0 до l=¥. Реальные тела имеют сплошной (диэлектрики) или линейчатый спектр излучения (газы, пары, некоторые металлы). На рис 7.1 сопоставлены зависимости I=f(l) для абсолютно черного и реального тел со сплошным и линейчатым (заштрихованные полосы) спектром. Обозначим e=I/I0, если e имеет одинаковое значение для всех длин волн, то тело называют серым. Величина e называется степенью черноты тела.
Плотность интегрального полусферического излучения абсолютно черного тела получим, проинтегрировав соотношение (7.6)
|
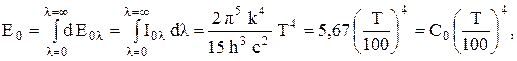(7.8)
где C0=5,67 вт/(м2×К4) – коэффициент излучения абсолютно черного тела.
Так как многие реальные тела имеют степень черноты e @ const, то плотность интегрального полусферического излучения серого тела равна
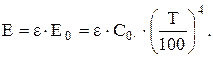(7.9)
Соотношение (7.8) называют законом Стефана-Больцмана, из которого следует, что плотность интегрального полусферического излучения абсолютно черного тела прямо пропорциональна четвертой степени его абсолютной температуры. Для реальных серых тел используют закон «четвертой степени» соотношение (7.9), где степень черноты e<1. Наибольшие отклонения от этого закона наблюдаются у газов и металлов. У металлов эта «степень» больше, а у газов – меньше четырех. Однако для расчетной оценки лучистых потоков используется соотношение (7.9), а несоответствие этой формулы действительной зависимости излучательной способности тела от температуры учитывается выбором соответствующей степени черноты.
Степень черноты e зависит от природы тела, температуры, степени шероховатости поверхности, а для металлов – еще от степени окисления поверхности. Степень черноты диэлектриков при комнатной температуре в большинстве случаев больше 0,8 и уменьшается с повышением температуры. У металлов степень черноты значительно ниже, чем у диэлектриков, и увеличивается с ростом температуры. Так, при комнатной температуре чистые стальные и чугунные поверхности имеют e=0,05¸0,45, а при высоких температурах e=0,7¸0,8.
Для тел, находящихся в тепловом равновесии (при одинаковой температуре), излучательная и поглощательная способности однозначно связаны. Рассмотрим, например, тепловое равновесие двух параллельных пластин, расположенных настолько близко друг к другу, что излучение каждой из них обязательно попадает на другую. Пусть одна из пластин – произвольное тело с излучательной и поглощательной способностями Е1 и А1. Вторая пластина абсолютно черное тело (А0=1). При тепловом равновесии количество излученной и поглощенной телом энергии одинаково. Первая стенка на каждый м2 поглощает Е0А1 вт, а ее излучение и отражение полностью поглощается абсолютно черной стенкой. Из условия теплового равновесия стенки следует
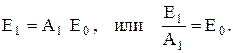(7.10)
Соотношение (7.10) справедливо не только для рассмотренной, но и для любой другой стенки, находящейся при той же температуре
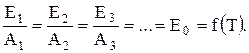(7.11)
Из этого выражения, которое называют законом Кирхгофа, следует, что отношение излучательной способности тела к его поглощательной способности одинаково для всех тел, находящихся при одной и той же температуре, и равно излучательной способности абсолютно черного тела при той же температуре. Таким образом, чем больше тело поглощает энергии, тем больше оно излучает, и для конкретной температуры абсолютно черное тело будет иметь наибольшую излучательную способность.
Диатермичные тела не поглощают лучистую энергию, следовательно, в соответствии с законом Кирхгофа они не могут излучать лучистую энергию. Если в уравнении (7.11) излучательную способность выразить через степень черноты по закону Стефана-Больцмана, то это уравнение будет иметь вид
(7.12)
Закон Кирхгофа справедлив и для монохроматического излучения. Если поглощательную способность монохроматического излучения обозначить через Аl, то для определенной длины волны имеем
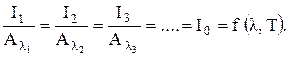(7.13)
Плотность интегрального полусферического излучения тела Е определяет излучение по всем направлениям полусферы. Излучательная способность тела по определенному направлению, составляющему с нормалью угол j, в единице телесного угла, характеризуется величиной Еj. При j=0, Еj.=En – интенсивность (яркость) излучения, вт/(ср×м2).
Закон Ламберта определяет зависимость излучаемой телом энергии в единицу времени от направления.
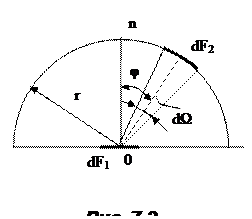
Если за единицу времени количество лучистой энергии передаваемое, как показано на рис. 7.2, элементарной площадкой поверхности тела dF1 на площадку dF2, расположенную на расстоянии r под углом j к нормали, обозначить через dQj, то по закону Ламберта
|
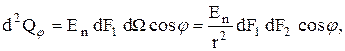(7.14)
где 
– пространственный угол, под которым площадка dF2 видна из точки О.
Пользуясь законом Ламберта, можно установить связь интенсивности (яркости) излучения или излучательной способности в направлении нормали с общей излучательной способностью тела
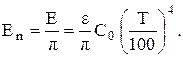(7.15)
Закон Ламберта точно удовлетворяется для абсолютно черных тел. Для реальных тел при j>600 действительные потоки лучистой энергии от шероховатых поверхностей несколько меньше, а от полированных металлических поверхностей несколько больше, чем рассчитанные по закону Ламберта.
При прохождении излучения через вещество происходит поглощение энергии излучения. Если элементарный поток монохроматического излучения входит в однородную и изотропную среду, имея интенсивность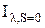 
, то на расстоянии S по направлению луча его интенсивность будет равна
(7.16)
а поглощательная способность среды на пути S составит
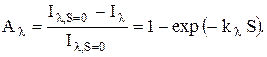(7.17)
Уравнения (7.16) и (7.17) выражают закон Бугера. Здесь kl – коэффициент поглощения (ослабления) вещества для лучей данной длины волны. Этот коэффициент зависит от физических свойств среды, ее температуры и длины волны. Для большинства твердых тел этот коэффициент большой, поэтому поглощение происходит в очень тонком слое. Газы обладают значительно большей «прозрачностью» для теплового излучения, поэтому поглощение энергии теплового излучение происходит в объеме газового тела.
