При соприкосновении пара с твердой стенкой, температура которой ниже температуры насыщения, происходит конденсация. Различают пленочную и капельную конденсации пара. Пленочная конденсация пара имеет место, когда жидкость смачивает твердую стенку, а капельная конденсация, когда не смачи-вает. Наиболее часто в технических устройствах встречается пленочная конден-сация пара. При конденсации выделившаяся скрытая теплота парообразования передается поверхности охлаждения. При пленочной конденсации пар отделен от стенки слоем конденсата, который оказывает термическое сопротивление тепловому потоку. Течение этой пленки по поверхности охлаждения может иметь ламинарный и турбулентный характер. При капельной конденсации возможен непосредственный контакт пара со стенкой, и поэтому теплообмен протекает во много раз более интенсивно, чем при пленочной конденсации.
Сначала рассмотрим теплоотдачу при конденсации насыщенного пара и ламинарном течении пленки конденсата. В этом случае плотность теплового потока можно записать двояко: по формуле теплопроводности и по закону теплоотдачи Ньютона-Рихмана
(6.10)
где d – средняя толщина пленки конденсата;
l – коэффициент теплопроводности конденсата;
a – средний коэффициент теплоотдачи.
Следовательно, для коэффициента теплоотдачи имеем
(6.11)
Из этой формулы видно, что уменьшение толщины пленки конденсата интенсифицирует теплообмен. Например, установка на вертикальной трубе конденсатоотводных колпачков через каждые 10 см приводит к увеличению коэффициента теплоотдачи в 2¸3 раза.
Расчетные формулы для определения коэффициента теплоотдачи при ламинарном движении пленки конденсата могут быть получены теоретическим и экспериментальным путем. Теоретическое решение задачи основано на определении толщины пленки конденсата в соотношении (6.11) из условия равновесия сил трения, тяжести, поверхностного натяжения и инерции для элементарного объема конденсата. Результаты опытного изучения теплоотдачи при конденсации для труб удовлетворительно согласуются с теоретическими решениями и обобщены уравнением подобия
(6.12)
в котором 
– число Галилея; 
– число Кутателадзе.
Для горизонтальных труб с=0,72; n=0,27; для вертикальных труб с=1,15 и n=0,85 при 
и с=0,068; n=0,33 при (Ga×Pr×K)ж>1015.
В качестве определяющей в этих формулах принята средняя температура пленки конденсата, на что указывает индекс «ж». В качестве определяющего размера для вертикальных труб выбирается высота, а для горизонтальных труб – диаметр.
Режим течения пленки конденсата можно оценить по числу Рейнольдса, выраженному через среднюю скорость жидкости wср и среднюю толщину пленки d. Еще У. Григуль обнаружил, что при Red >300 фактические коэффициенты теплоотдачи больше расчетных. В настоящее время полагают, что переход в турбулентный режим при течении пленки конденсата происходит при критическом значении Reкр = 400. При стационарном режиме теплообмена теплота конденсации равна теплу, переданному в стенку. Поэтому для поверхности высотой х и шириной 1 м можно записать баланс тепла в виде
Если подставить значение d из этого соотношения в выражение для числа Рейнольдса, то получим
(6.13)
Как видно, искомый коэффициент теплоотдачи входит в число Рейнольдса, поэтому в уравнениях подобия (критериальных уравнениях) это число является определяемым. Хорошо совпадает, например, с опытными данными для осредненной теплоотдаче при пленочной конденсации неподвижного пара на вертикальной поверхности при ламинарном течении пленки конденсата уравнение Нуссельта с учетом зависимости физических свойств конденсата от температуры
(6.14)
где
индекс «н» обозначает, что в безразмерные величины входят физические свойства конденсата, выбранные по температуре насыщения.
При расчете средней теплоотдачи турбулентного течения конденсата нужно учесть, что в верхней части стенки на ламинарном участке уже образовался определенный слой конденсата. Учитывая это, и полагая Reкр=400 и Zкр=2300, формула для расчета среднего коэффициента теплоотдачи при конденсации чистого неподвижного пара на вертикальной поверхности и смешанном течении пленки конденсата принимает следующий вид
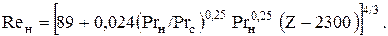(6.15)
Если по граничным условиям второго рода на стенке задана плотность теплового потока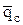 
,то, учитывая, что 
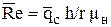, формулу (6.15) удобнее применять в следующем преобразованном виде
(6.16)
Определяющей является температура насыщения (исключая Prc, который рассчитывают по температуре стенки), определяющим размером – высота стенки h. Все физические параметры берутся для конденсата. Если давление пара велико, то плотность пара соизмерима с плотностью конденсата. Поэтому в приведенных выше уравнениях подобия число Галилея Ga нужно заменить числом Архимеда 
Наклон поверхности по отношению к вертикали уменьшает скорость течения пленки конденсата и уменьшает коэффициент теплоотдачи. Если угол поверхности с вертикалью составляет jо, то коэффициент теплоотдачи наклонной поверхности можно определить по формуле
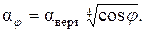(6.17)
Влияние перегрева пара на коэффициент теплоотдачи при конденсации невелико. В выше приведенных формулах для расчета теплоотдачи в условиях конденсации перегретого пара вместо теплоты испарения r надо подставлять r+Di, где Di – теплота перегрева пара.
Вынужденное движение пара оказывает влияние на коэффициент теплоотдачи при пленочной конденсации. Движение пара вдоль вертикальной поверхности вниз вследствие трения на границе с конденсатом ускоряет движение пленки. Толщина ее уменьшается, и коэффициент теплоотдачи увеличивается. Если направление движения пара противоположно направлению течения конденсата, то скорость пленки уменьшится. При этом возрастет ее толщина и уменьшится коэффициент теплоотдачи. Однако при больших скоростях пара возможно не только торможение пленки конденсата, но и срыв ее с поверхности. При таких срывах пленки коэффициент теплоотдачи возрастает.
При ламинарном течении пленки конденсата и вынужденном течении пара в трубе локальный коэффициент теплоотдачи равен
(6.18)
где aох – коэффициент теплоотдачи для неподвижного пара;
где 
средняя в сечении х скорость пара; et – поправка, учитывающая зависимость физических свойств конденсата от температуры (смотри формулу (6.14)). Числа Reпd изменялись в опытах от 1,8×103 до 17×103, этому соответствовала скорость пара от 3,6 до 33,5 м/с. Температурный напор изменялся от 8 до 60 0С. При y<35 расчет можно вести по формулам для неподвижного пара. Физические параметры пара и конденсата, что соответственно обозначено индексами «п» и «ж», выбирались по температуре насыщения.
При турбулентном течении конденсата среднее значение коэффициента теплоотдачи для режима неполной конденсации пара из пароводяной смеси определяется формулой
(6.19)
где x1=(Gп/Gсм)вх и x2=(Gп/Gсм)вых массовые расходные паросодержания во входном и выходном сечении рассматриваемого участка трубы. Для стальных труб с=0,024, для латунных с=0,026, для медных с=0,032. В формуле (6.19) для чисел подобия имеем
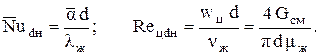
Все физические параметры выбираются по температуре насыщения. Индексы «ж» и «п» обозначают, что данная величина является физическим параметром соответственно жидкости и пара. При конденсации движущегося пара в трубе значение критического числа Рейнольдса может быть принято примерно равным 200.
Коэффициент теплоотдачи при конденсации движущегося пара, обтекающего горизонтальную трубу (течение пара сверху вниз), может быть рассчитан для ламинарного течения конденсата по формуле
(6.20)
где 
средний коэффициент теплоотдачи при конденсации неподвижного пара;
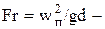число Фруда;
wп – скорость набегающего на трубу пара;
d – наружный диаметр трубы;
g – ускорение свободного падения;
число Кутателадзе;
DТ=Тн-Тс – температурный напор;
r, m – плотность и коэффициент динамической вязкости; 
Конденсационные аппараты, как правило, имеют не одну трубу, а пучок труб. Трубы в пучке обычно размещаются в шахматном или коридорном порядке. Процессы конденсации на наружной поверхности одиночной горизонтальной трубы, а также труб, собранных в пучок, различны. Это различие обусловлено двумя факторами: уменьшением скорости пара при его движении в пучке из-за частичной конденсации и утолщение пленки конденсата за счет последовательного стекания конденсата с трубы на трубу. Уменьшение скорости пара по мере его продвижения через пучок приводит к уменьшению теплоотдачи при возрастании номера ряда. Конденсат стекает с трубы отдельными каплями или струйками. Капли, попадая на ниже расположенную трубу, с одной стороны, временно утолщают пленку в месте падения, растекаясь затем по поверхности, с другой – возмущают течение пленки, что может привести к турбулентному течению. Для первого ряда пучка горизонтальных труб, обтекаемых сверху вниз чистым водяным паром (без примеси газов), средний коэффициент теплоотдачи 
вычисляется по уравнению
(6.21)
где 
– коэффициент теплоотдачи для неподвижного пара;
wп – скорость пара в узком сечении горизонтального ряда труб.
Определяющей является температура насыщения. Индексы «ж» и «п» соответственно относятся к жидкости и пару. Это уравнение справедливо при значениях давления р=4,6¸103 кПа; температурном напоре DТ=0,5¸150С и 400< 
<6000.
Средний коэффициент теплоотдачи для всего пучка горизонтальных труб, имеющего одинаковое сечение по высоте, приближенно равен
(6.22)
где 
– относительный коэффициент теплоотдачи для первого ряда, вычисляемый по уравнению (6.21);
n – число рядов труб по высоте шахматного пучка;
D=(Gвх-Gвых) / Gвх – степень конденсации пара;
Gвх и Gвых – массовые расходы пара на входе и выходе из пучка.
Как указывалось выше, капельная конденсация имеет место, если конденсат не смачивает поверхность теплообмена. По мере роста капли непрерывно сливаются, освобождая какую-то часть поверхности стенки. Многократное слияние и непрерывно идущий процесс конденсации увеличивают капли до отрывного диаметра, при котором они скатываются под действием силы тяжести. Строго говоря, капельная конденсация пара является нестационарным процессом. Ее можно рассматривать стационарной в том смысле, что осредненные по времени характеристики процесса не изменяются. При первичном соприкосновении пара с поверхностью стенки образуется адсорбционный слой жидкой полимолекулярной пленки. Она находится в силовом электрическом поле молекул твердой стенки. Поэтому ее свойства отличны от свойств этой же жидкости вдали от границы раздела фаз в объеме. Такую пленку жидкости, толщиной в доли микрометра, называют тонкой. Она находится под избыточным давлением П, которое называют расклинивающим. Расклинивающее давление обратно пропорционально примерно кубу толщины пленки П~d-3. Для не смачиваемых поверхностей расклинивающее давление отрицательно. Поэтому поверхности тонкой пленки притягиваются друг к другу и тем больше, чем тоньше пленка. Локальное утонение пленки, например, на выступах шероховатости стенки приводит к увеличению расклинивающего давления в этом месте по сравнению с соседними участками. В результате жидкость перемещается на эти участки, где и образуются первичные капли, размеры которых больше эффективного радиуса действия межмолекулярных сил. Равновесное давление насыщенного пара над выпуклой поверхностью раздела фаз больше, чем над плоской поверхностью. Конденсация пара на поверхности сферической капли с радиусом R, взвешенной в паре, возможна при условии, что R>Rк, где Rк – критический (минимально возможный) радиус кривизны поверхности раздела фаз. Разность давлений в тонком сферическом слое конденсата и в паре с учетом выше изложенного может быть описана уравнением
(6.23)
где s – коэффициент поверхностного натяжения на границе жидкость – пар.
При этом критическое переохлаждение пара DТк=ТS–Тс в случае сферических пленок описывается уравнением
(6.24)
Первое слагаемое в правой части учитывает капиллярные эффекты первого рода (поверхностное натяжение), а второе – капиллярные эффекты второго рода (расклинивающее давление). Если существующее переохлаждение пара DТ больше расчетного критического переохлаждения DТк, то конденсация термодинамически возможна. Для толстых пленок R>Rк расклинивающее давление П®0 и уравнения (6.23) и (6.24) при П=0 переходят в известные уравнения Лапласа и Томсона. В общем случае на поверхности стенки в каждый момент существует множество капель, радиус которых изменяется от критического Rк до отрывного R0. Спектр размеров капель может быть описан дифференциальной функцией распределения капель по размерам j(R)=dn/dR, где dn – число капель с радиусом от R до R+dR, приходящиеся на единицу поверхности стенки. Так как процесс капельной конденсации квазистационарный, то j(R)=const. Приращение объема капли в единицу времени за счет конденсации пара определяется уравнением
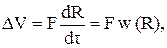(6.25)
где F – поверхность капли;
w(R) – функция скорости роста капли. При этом выделяется теплота фазового перехода.
Каплю на поверхности стенки будем считать полусферой. Для капель с радиусами от R до R+dR выделенная теплота фазового перехода, отнесенная к единице поверхности стенки и к единице времени, равна
(6.26)
Если проинтегрировать это соотношение, то для средней плотности теплового потока получим
(6.27)
где qco – теплота, выделившаяся при образовании первичных капель, которой в силу ее малости пренебрегают.
Таким образом, для теоретического расчета плотности теплового потока на стенке qc или коэффициента теплоотдачи a= qc / DТ при капельной конденсации необходимо знать функции роста капель w(R) и распределения по размерам j(R). Скорость роста полусферической капли, когда основным термическим сопротивлением является термическое сопротивление теплопроводности капли, определяется приближенным уравнением
(6.28)
Кроме описанного теоретического подхода, для определения коэффициента теплоотдачи широко используется непосредственный эксперимент. Однако, как это было показано в главе 5, посвященной подобию процессов теплообмена, теоретическое описание позволяет выбрать масштабы приведения уравнений к безразмерному виду и получить систему чисел подобия. Так, описанная выше теория капельной конденсации позволяет выбрать в качестве линейного размера критический радиус капли из соотношения (6.24) при П = 0, а из формулы (6.28) условную скорость роста конденсированной фазы 
при отводе теплоты фазового перехода теплопроводностью.
Средний коэффициент теплоотдачи при капельной конденсации неподвижного пара можно определить из опытных уравнений подобия
при 
(6.29)
при 
(6.30)
где
В этих формулах физические свойства конденсата выбираются по температуре насыщения TS. В формулы температура подставляется в градусах Кельвина. Число подобия Пк можно трактовать как отношение термокапиллярных сил к силам вязкости. Его можно представить в виде
где 
– температурный коэффициент поверхностного натяжения;
– число Лапласа.
Теплоотдача при капельной конденсации пара начинает зависеть от скорости пара уже при сравнительно небольшой ее величине при малых температурных напорах DТ~1¸2 0К. При значительных температурных напорах средний коэффициент теплоотдачи движущегося пара мало отличается от среднего коэффициента теплоотдачи неподвижного пара. Опытные данные для коэффициента теплоотдачи при движении пара обобщены в виде следующего уравнения подобия
(6.31)
где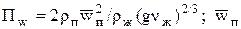 
– средняя скорость пара на расчетном участке; – средний коэффициент теплоотдачи для неподвижного пара. Опытные данные получены при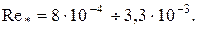 
Если пар содержит примеси неконденсирующихся газов, то эти газы скапливаются около поверхности охлаждения и резко уменьшают интенсивность теплообмена. Так, 2 % содержания воздуха в паре приводит к уменьшению коэффициента теплоотдачи в три раза.
Теплообмен излучением
Основные понятия и определения
В любом теле при температуре большей, чем 0оК некоторая доля внутренней тепловой энергии трансформируется в энергию электромагнитного поля, которое, покидая тело, распространяется в окружающем его пространстве. Это электромагнитное излучение, попадая на другие тела, частично поглощается, вновь трансформируясь при этом во внутреннюю тепловую энергию. Механизм этой трансформации станет понятным, если учесть, что внутренняя тепловая энергия представляет собой кинетическую энергию хаотического движения микрочастиц тела. Но скорость любой микрочастицы хаотически изменяется во времени. Микрочастицы имеют положительные и отрицательные электрические заряды. Из физики известно, что ускоренное (замедленное) движение электрических зарядов приводит к поглощению (излучению) электромагнитных волн. Помимо волновых свойств, электромагнитное излучение обладает также корпускулярными свойствами. Лучистая энергия испускается и поглощается телами не непрерывно, а отдельными дискретными порциями – квантами света или фотонами. Таким образом, электромагнитное излучение и поглощение имеет двойственный характер, так как обладает свойствами непрерывности поля электромагнитных волн и свойствами дискретности, типичными для фотонов. Синтезом обоих свойств является представление, согласно которому энергия и импульсы сосредоточиваются в фотонах, а вероятность нахождения их в том или ином месте пространства – в волнах. Электромагнитное излучение характеризуется длиной волны l или частотой колебаний n=с/l, где с=2,9979×108 м/с – скорость света в вакууме. Все виды электромагнитного излучения имеют одинаковую природу и различаются лишь длиной волны. Большинство твердых и жидких тел имеют сплошной (непрерывный) спектр излучения, т.е. излучают энергию всех длин волн от 0 до ¥. К твердым телам, имеющим непрерывный спектр излучения, можно отнести непроводники и полупроводники электричества, металлы с окисленной шероховатой поверхностью. Газы, пары и металлы с полированной поверхностью имеют прерывистый (селективный) спектр излучения. Излучение всех тел зависит от температуры. С увеличением температуры тела его энергия излучения увеличивается, так как увеличивается внутренняя тепловая энергия тела. Важно отметить, что, если в систему входят разные тела и температуры их одинаковы, то тела в этой системе будут находиться в тепловом равновесии. Каждое из этих тел будет излучать, и поглощать электромагнитную энергию, но результирующий перенос этой энергии между телами будет равен нулю. Когда температуры тел не одинаковы, то результирующий перенос электромагнитной энергии уже не равен нулю и направлен от тел с большей температурой к телам с меньшей температурой. В процессах теплообмена излучением зависимость его от разности температур тел значительно больше, чем в процессах теплопроводности и конвекции. Поэтому при очень больших перепадах температур между телами, даже разделенных вакуумом, основным видом переноса теплоты может быть теплообмен излучением. Процесс превращения внутренней тепловой энергии в лучистую энергию происходит во всем объеме тела. Но лучистая энергия частиц, расположенных далеко от поверхности тела, часто поглощается самим телом, а в окружающую среду попадает только энергия, испускаемая тонким поверхностным слоем. Твердые и жидкие тела, как правило, имеют значительные излучательную и поглощательную способности. У них в процессах лучистого теплообмена участвуют лишь тонкие поверхностные слои: у непроводников электричества они составляют около 1 мм, для проводников электричества 1мкм. Полупрозрачные тела (плавленый кварц, стекло и т. п.), а также газы и пары характеризуются объемным излучением, в котором участвуют все частицы объема тела.
Если из общего количества лучистой энергии Q, падающего на тело за единицу времени, поглощается QA, отражается QR и проходит сквозь тело QD, то
(7.1)
Отношение QA/Q=A называется поглощательной способностью, отношение QR/Q=R – отражательной способностью, а отношение QD/Q=D – пропускательной способностью:
A+R+D=1. (7.2)
Тело, поглощающее всю падающую на него энергию, называется абсолютно черным. Для такого тела А=1 и R=D=0. Абсолютно черных тел в природе нет и поэтому для реальных тел А<1. Способность тела поглощать лучистую энергию зависит от природы тела, состояния его поверхности и температур источника излучения и самого тела. При температурах, близких к комнатной, поглощательная способность большинства неметаллических материалов больше 0,8, но она может значительно уменьшаться с увеличением температуры. Чистые металлические поверхности поглощают значительно меньше лучистой энергии, но с увеличение температуры их поглощательная способность увеличивается примерно пропорционально 
температуры в градусах Кельвина излучающей и поглощающей поверхностей). Окисление металлической поверхности приводит к увеличению ее поглощательной способности. При умеренных температурах источника излучения цвет поверхности не определяет ее поглощательную способность. В этих условиях белые тела так же хорошо поглощают лучистую энергию, как и темные. Так, например, снег имеет А=0,985.
Тела, отражающие всю падающую на них энергию, называются абсолютно белыми. В этом случае R=1 и A=D=0. Если при отражении угол падения излучения равен углу отражения, то такие тела называют зеркальными. Для реальных тел R<1. Большинство твердых тел не пропускают лучистую энергию и для них A+R=1. Для них все факторы, увеличивающие поглощательную способность, одновременно уменьшают отражательную способность поверхности.
Тела, пропускающие всю падающую на них лучистую энергию, называются диатермичными. Для них D=1 и R=A=0. Наибольшей пропускной способностью обладают газы. Например, значительный слой воздуха можно считать диатермичным.
Излучение называется монохроматическим, если оно отвечает определенной частоте колебаний или длине волны (точнее, узкому интервалу длин волн). Излучение, отвечающее длинам волн от 0 до ¥, называется интегральным. Для монохроматического излучения из уравнения (7.2) имеем
(7.3)
Для одного и того же тела при различных длинах волн величины Al, Rl и Dl могут иметь отличные значения. Так, обычное стекло хорошо пропускает световые лучи (l=0,4¸0,8 мк), но не пропускает ультрафиолетовые и инфракрасные лучи.
