Завдання на розрахунково-графічну роботу

ЧОРНОМОРСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ

Імені Петра Могили

ПРОЕКТУВАННЯ ТА АНАЛІЗ

АКТИВНОГО ЕЛЕКТРИЧНОГО ФІЛЬТРА

Методичні вказівки до виконання

розрахунково-графічного завдання

з дисципліни «Методи і засоби реєстрації та відновлення інформації»

для студентів спеціальності

6.090900 "Медичні прилади і системи"

Миколаїв - 2009

ВСТУП

Передача і обробка цифрових сигналів електрозв'язку, сигналів радіо і телебачення і так далі вимагають створення електронних ланцюгів, які в певній смузі частот володіли б наперед заданими властивостями амплітудно-частотних і фазо-частотних характеристик (АЧХ і ФЧХ). Методи проектування і аналізу таких пристроїв відносяться до традиційних методів теорії ланцюгів.

Розрахунково-графічне завдання присвячене поглибленому вивченню цих методів на прикладі проектування активного електричного фільтру.

Електричним фільтром називається електричний ланцюг, призначений для виділення коливань в певному діапазоні частот. Діапазон частот, що пропускається фільтром називається смугою прозорості (пропускання) або СП. Область частот, в якій всі частоти пригнічуються із заданим ослабінням, називається смугою затримання або СЗ.

Відповідно до діапазону частот, що пропускаються фільтром, вони діляться на наступні типи (fзр - частота зрізу АЧХ):

ФНЧ - фільтри нижніх частот - ПП від 0 до fзр;

ФВЧ - фільтри верхніх частот - ПП від fзр до Г;

СФ - смугові фільтри - СП від fзр1 до fзр2;

ЗФ - фільтр, що загороджує, - СЗ від fзр1 до fзр2;

ФФ - фазові фільтри - СП від 0 до Г і заданої корекції фази.

Залежно від вхідних в них компонентів фільтри підрозділяють на:

реактивні або LC-фільтри;

резистивно-ємкісні або RC-фільтри;

активні або ARC-фільтри.

У роботі студент повинен спроектувати ARC-фільтр на основі ідеального операційного підсилювача (ОП). Тип фільтру визначається розташуванням нулів і полюсів, по ним же обчислюються параметри елементів.

Проектована схема і вигляд вхідного сигналу задаються відповідно до номеру варіанту. Теоретичні передумови і методи синтезу і аналізу вибіркових ланцюгів на основі ОП наводяться в [1, 2, 3, 4].

ПРОЕКТУВАННЯ ARC-ФІЛЬТРА

Розглянемо загальні принципи реалізації передавальної функції другого порядку

(1)

за допомогою ОП, охопленого зворотним зв'язком (ЗЗ). Пасивна частина схеми є багатополюсником, що складається з резистивних і ємкісних елементів (рис.1)

Рис.1 Электронна схема на основі ОП з ЗЗ

Складемо рівняння пасивного триполюсника у Y-формі.

(2)

За умови ідеального ОП його вхідний ланцюг (затиски 3-3’) не споживає струму, тобто I ₃ = 0. Враховуючи, що U ₂ = - K ₀ U ₃, з третього рівняння системи (2) отримаємо

. (3)

При K ® ¥ передавальна функція ланцюга визначається лише параметрами RC-кола:

. (4)

Передбачимо, що RC-багатополюсник має структуру, що показана на рис.2 б і складається з п'яти пасивних компонентів (R- і C-елементів)

Скористаємося властивостями ідеального ОУ: різниця потенціалів між його вхідними затисками дорівнює нулю, тобто U ₃ = 0 (см.рис.2). Це означає, що потенціал затиску 3 дорівнює нулю. Складемо рівняння вузлів 4 і 3:

а) б)

Рис.2. Пасивний триполюсник (а) і його 5-елементна конфігурація (б)

Вирішуючи друге рівняння цієї системи відносно вихідної напруги U ₂, тобто , і, підставляючи результат в перше рівняння, після не складних перетворень отримаємо вираження для коефіцієнта передачі по напрузі:

(5)

де

Задаючи як провідність Y _i провідність ємності pC _i або провідність опору 1/ R _i, можна скласти необхідний вигляд передавальної функції K _U(p).

1.1 НЧ-фільтр другого порядку. Його передавальна функція має вигляд:

(6)

Аби права частина рівняння (5) відповідала дробу (6), слід вибрати як ємкості елементи Y2 і Y5, останні представити опорами. Тоді передавальна функція може бути виражена через параметри елементів (RC) -схеми (рис.3):

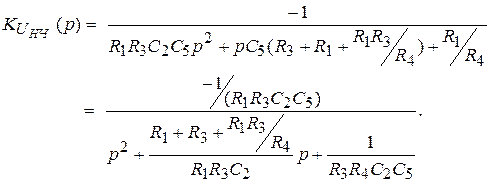(7)

Таким чином, із зіставлення функцій (6) і (7) виводиться система з трьох рівнянь для визначення параметрів елементів пасивного триполюсника:

(8)

Оскільки невідомих параметрів п'ять, то два з них можуть задаватися довільно. Зазвичай вибирається якась ємкість, наприклад C₂ = C₀ з нормального ряду параметрів і постійна часу t₀ = R₁C₂, т.е. R₁ = t₀ / C₀. Параметри останніх елементів знаходяться підстановкою C₂ та R₁ у систему (8) з подальшим її рішенням:

(9)

Рис. 3. Активний НЧ-фільтр другого порядку

1.2. СФ другого порядку. Передавальна функція смугового фільтру

(10)

Також може бути реалізована за допомогою пасивного трехполюсника в конфігурації, зрисованої на рис.2,б. Якщо вибрати провідність Y₁ и Y₅ ємнісними, тобто Y₁ = pC₁, Y₅ = pC₅, а останні елементи резистивними, то передавальна функція може бути представлена через параметри елементів (рис.4):

(11)

Як і в попередньому пункті, задаючись C₁ = C₀, b = С₁ /С₅, С₅ = С₁ /b, вирішуємо систему трьох рівнянь для визначення параметрів інших елементів:

(12)

(13)

Рис. 4. Активний СФ другого порядку

1.3. ВЧ-фільтр другого порядку має передавальну функцію

(14)

яка так само може бути реалізована на ОП з триполюсником у вигляді однорідних R і C-елементів. Чисельник дробу (14), рівний результату множення Y₁Y₃, задає ємнісний характер елементів Y₁ = pC₁ и Y₃ = pC₃. Для здобуття в знаменнику дробу доданку з другою мірою від p(див. вираз (5)) необхідно задати ще один ємнісний елемент, а саме Y₄ = pC₄. Останні елементи мають бути резистивними (рис.5.): Y₂ = 1/R₂, Y₅ = 1/R₅.

Рис. 5. Активний ФВЧ другого порядку

Коефіцієнт передачі по напрузі, виражений через параметри елементів, має вигляд:

(15)

Зіставивши вирази (14) і (15), можна отримати систему, за допомогою якої визначаються параметри елементів схеми ФВЧ:

(16)

Задаючись додатковими умовами С₁ = С₀ и t = C₄R₅ до системи (16) отримаємо наступний обчислювальний алгоритм:

(17)

АНАЛІЗ АКТИВНИХ ФІЛЬТРІВ

У завданні є пункт дослідження частотних характеристик активного фільтру, побудованого на основі ОУ. Розглянемо деякі аспекти такого аналізу, що проводиться з використанням обчислювальної техніки.

2.1. Схема заміщення реального ОП приведена на рис.6.

Рис.6. Схема заміщення ОП з однією частотою загасання

Вона відображує кінцеві вхідні R_В_х_– и R_В_х₊ і вихідне R_В_их опори і коефіцієнт посилення K₀, а також обмеженість частотного діапазону ОП. Ці параметри приведені в довідниках [7,8]. Внутрішній RC-коло моделює поступове зменшення коефіцієнта посилення K_U(jw) із зростанням частоти w згідно із законом

(18)

по якому можна визначити параметри цього RC-кола. При відомих значеннях коефіцієнта посилення на нульовій частоті K₀ та f_ЕУ – частоті одиничного посилення - постійна часу RC -кола

. (19)

Вибір значення параметрів R і C визначається лише тим, аби їх результат множення дорівнював t_RC.

Заміна ідеального ОП схемою заміщення, змальованою на рис.6, дає можливість провести дослідження реального вибіркового ланцюга при роботі на задане навантаження Z_H (рис.7).

2.2. Метод вузлових потенціалів є найбільш відповідним в нашому випадку методом формування рівнянь електричної рівноваги ланцюга. Для спрощення розрахунків слід замінити джерела напруги на еквівалентні джерела струму.

Рис.7. Эквівалентна схема ARC-кола

Система має п'ять рівнянь - по числу незалежних вузлів схеми:

Вузли
	Y_E + Y₁		-Y₁
2	0	Y₄+Y₅+Y_H+Y_В_их	-Y₄	-Y₅	-K₀Y_В_их
	-Y₁	-Y₄	Y₁+Y₂+Y₃+Y₄	-Y₃
		-Y₅	-Y₃	Y₃+Y₅+Y_ВХ-
				-1/R	1/ R+jwC

* (20)

Всі потенціали вузлів збігаються з напругою вузлів, це враховано в цій системі.

Розрахунок вихідної напруги U₂ на опір навантаження при рішенні системи (20) може бути виконаний, наприклад, за допомогою математичного пакету MATHCAD або систем моделювання DESIGNLAB(PSpice), Electronic Work Banch, MICROCAP. Для здобуття частотних залежностей необхідно циклічно вирішувати систему (20) з кроком D w у певному діапазоні частот, наприклад, при аналізі частотних характеристик НЧ-фільтру від 0 до w_В.

2.3. Часові характеристики (імпульсна q(t) і перехідна h(t)) знаходяться безпосередньо по коефіцієнту передачі K_U(p), точніше по його нуль-смуговому представленню. Передбачимо, що обчислені полюси , визначувані як коріння полінома знаменника дробу (1):

где (21)

Якщо позначити реальну і уявну складові полінома чисельника при підстановці в нього полюса p₁ у вигляді:

(22)

то при підстановці комплексно зв'язаного полюса p₂ = p₁^* значення полінома чисельника так само буде комплексно зв'язаним:

(23)

Для простих полюсів зворотне перетворення Лапласа від K_U(p) знаходиться досить просто (наслідок вживання вирахувань):

(24)

де N - повна кількість полюсів.

З врахуванням позначень (22) і (23) імпульсна характеристика досліджуваної схеми набере вигляду:

(25)

2.4. Нуль-полюсне зображення вхідної дії, заданої у вигляді кусочно-ламаної залежності (рис.8,а) легко отримати по його похідній (рис.8,б). Прямокутний імпульс амплітудою U₀ /t₁ визначений на інтервалі (0, t₁) має зображення

(у формулі приведено позначення гіперболічного синуса sh(x) = (e^x –e^-^x)/2)

Рис. 8. Кусочно-ламана залежність (а) і її похідна (б).

Аналогічно другий прямокутний імпульс R₂(t) має зображення

Зображення дії є сума зображень імпульсів R₁(p) та R₂(p), ділена на p (оскільки функція e(t) є інтеграл від її похідної de(t) /dt):

(26)

Комплексно-значна функція E(p) не має полюса в нулі (p = 0), оскільки вираження в квадратних дужках при p® 0 так само прагне до нуля, тобто

lim E(p) = S < ¥,

p® 0 (27)

де S – площа під кусочно-ламаною залежністю e(t).

ЗАВДАННЯ НА РОЗРАХУНКОВО-ГРАФІЧНУ РОБОТУ

3.1 Вибрати по табл.1 варіант розташування нулів і полюсів ланцюга (по останній цифрі номера в заліковій книжці).

Таблица 1

Остання цифра номера	Полюси p ₁= p ₂^*	Нулі p ₀₁, p ₀₂	Коеффіцієнт Н
	- 3000 ± 2000 j	-	-10 ⁸
	- 3000 ± 3000 j	-	-2×10 ⁸
	- 4000 ± 6000 j	-	-10 ⁸
	- 5000 ± 6000 j	-	-10 ⁹
	- 5000 ± 6000 j	p ₀₁ = p ₀₂ = 0	-1
	- 6000 ± 8000 j	p ₀₁ = p ₀₂ = 0	-2
	- 10000 ± 8000 j	p ₀₁ = p ₀₂ = 0	-1
	- 8000 ± 8000 j	p ₀₁ = p ₀₂ = 0	-5
	- 1200 ± 3000 j	p ₀₁ = 0	-10 000
	- 1800 ± 5000 j	p ₀₁ = 0	-15 000

3.2 Визначити вигляд коефіцієнта передачі по напрузі K _U(p) і тип вибіркового ланцюга (формули 6, 8 або 12).

3.3. Записати комплексну частотну характеристику ланцюга K (jw) і відповідні їй амплітудно-частотну K (w) і фазо-частотную j (w) характеристики.

3.4. Розрахувати і побудувати графіки K (w), j (w) і годографа K (j (w))у діапазоні частот від 0 до 10 f _П, де f _П = Im (p ₁)/(2p). Знайти граничні частоти за умов:

K (f _ГР) = K (0)/ Ö2 (ФНЧ),

K (f _ГР) = K (¥)/Ö2 (ФВЧ),

K (f_{ГР 1,2}) = K _MAX/Ö2 (СФ).

3.5. Спроектувати на основі ідеального ОП принципову схему вибіркового ланцюга і розрахувати її параметри. Використовувати приклади схем, зрисовані на рис.3, рис.4, рис.5. При негативних значеннях параметрів елементів узяти схему з Додатка 2.

3.6. Скласти по методу вузлових потенціалів систему рівнянь електричного балансу ланцюга з реальним ОП. Обчислити частотні залежності А- параметрів (модуль і фазу) вибіркового ланцюга в діапазоні від 0 до f _В. Параметри реального ОУ узяти з Додатка 1 відповідно до номера варіанту.

3.7. Визначити імпульсну h(t) і перехідну g(t) характеристики ланцюга на основі ідеального ОП. Розрахувати і побудувати графіки цих залежностей. Визначити час встановлення процесу t _У з умови h (t _У) = 0.9 h (t ® ¥) чи h (t _У) = 0.1 h _МАКС.

3.8. Методом інтеграла накладення з врахуванням знайдених часових характеристик визначити відгук на виході ланцюга для заданої дії (див. рис. 8а), параметри якої узяти з табл. 2. Побудувати графіки дії і відгуку на одному рисунку в однаковому масштабі.

Таблиця 2

Передостання цифра номеру	U _MAX, В	t ₁	t ₂	t ₃
			0.75t	t
		0.25t	0.5t	t
	0.5	0.25t	0.75t	t
	1.5	0.1t	0.8t	t
	2.5	0.5t	0.5t	t
		0.2t	0.7t	t

Тут величина .

3.9. Скласти нуль-полюсне представлення дії і відгуку, записавши зображення по Лапласу від вхідної дії і визначивши по ньому зображення відгуку.

3.10. Знайти спектральну щільність відгуку і побудувати залежності її модуля і фази від частоти в діапазоні від 0 до f _В.

3.11. Визначити оригінала від зображення відгуку по зворотному перетворенню Лапласа і порівняти його з результатами п.3.8.

3.12. Розрахувати і побудувати енергетичні спектри дії і відгуку на одному графіку. Тут же побудувати графік нормованого квадрата модуля коефіцієнта передачі аналізованого ланцюга.