МЕТОДИЧНІ ВКАЗІВКИ
до лабораторних робіт
з дисципліни “Метрологія”
для студентів спеціальності 6.050801
"Мікроелектроніка і напівпровідникові прилади"
денної й заочної форм навчання
Методичні вказівки до лабораторних робіт з дисципліни “Метрологія” для студентів спеціальності 6.050801 "Мікроелектроніка і напівпровідникові прилади" денної й заочної форм навчання /Укл.: А.В. Бабіч.- Запоріжжя: ЗНТУ.-2013.- с.
Укладач: А.В. Бабіч, доц., канд.фіз.-матем.наук
Рецензент: Г.В.Сніжной, доц., канд.фіз.-матем.наук
Відповідальний за випуск: Г.В.Сніжной, доц., канд.фіз.-матем.наук
Затверджено
На засіданні кафедри
Мікроелектроніка і
напівпровідникові прилади”
Протокол №
Від 2013 р.
ЗМІСТ
| 1 Лабораторна робота №1 “Первинна обробка експериментальних даних. Визначення похибок” | |
| 2 Лабораторна робота №2 “Зондовіметоди вимірювання електропровідності напівпровідникових матеріалів” | |
1 ЛАБОРАТОРНА РОБОТА №1 “ПЕРВИННА ОБРОБКА ЕКСПЕРИМЕНТАЛЬНИХ ДАНИХ. ВИЗНАЧЕННЯ ПОХИБОК”
Мета роботи: ознайомитисяз теорією похибок;навчитися обробляти дані експерименту.
Вступ
Внаслідок неточності вимірювальних приладів, неповноти наших знань, труднощів урахування всіх побічних явищ при вимірюванні, неминуче виникають похибки. Тому задача вимірювань полягає не в пошуку "істинного" значення вимірюваної величини, а у встановленні інтервалу значень, усередині якого знаходиться вимірювана величина. Теорія погрішностей показує, як варто вести вимірювання й їх обробку, щоб величина цього інтервалу була найменшою.
Вимірювання можуть бути прямими і непрямими. Прямі – це такі, при яких вимірювана величина порівнюється безпосередньо з деяким еталоном. Непрямі вимірювання характерні тим, що такого прямого порівняння вимірюваної величини з еталоном провести неможливо. Тому використовуються зв'язки вимірюваної величини з іншими, котрі можна вимірювати прямим шляхом.
1.1 Загальні відомості з теорії похибок
1.1.1 Класифікація похибок
Похибки можна розділити на промахи, систематичні і випадкові похибки.
Промахи - очевидно помилкові вимірювання: невірно узятий відлік, невірні записи результату, неправильне включення приладу і т.п.
Систематичні похибки - похибки, зумовлені однією і тією ж причиною, які залишаються постійними або закономірно змінюються під час повторних вимірювань однієї і тієї ж величини. Причиною появи таких погрішностей є: неправильне градуювання, наближена розрахункова формула чи метод, неправильне вимірювання і т.п. Їх можна врахувати, якщо не можна усунути.
Випадковими називають похибки, викликані дуже великим числом причин, врахувати які неможливо, тому що вони незалежно один від одного впливають на кожне вимірювання. Обмежена точність і чутливість приладів, що контролюють умови вимірювання, недосконалість наших органів почуттів, зовнішні умови, що змінюються, і т.п. - усе це приводить до появи випадкових погрішностей. Їх можна звести до мінімуму, але їх неможливо позбутися. Випадкові похибки можна оцінити, використовуючи так звану теорію помилок, яка є одним з розділів теорії ймовірності.
Похибки можна виразити у вигляді абсолютної величини (абсолютна похибка) і відносної величини. Перша показує величину інтервалу значень, у якому може знаходитися вимірювана величина, і тому є розмірною величиною, друга - показує частку цього інтервалу щодо вимірюваної величини. Відносну похибка часто виражають у відсотках.
1.1.2 Основи теорії похибок (погрішностей)
Якщо зроблено досить багато незалежних вимірювань деякої величини в умовах, що виключають промахи і систематичні похибки, а1, а2, а3,…, аn,…, ai, то “істинним” значенням вимірюваної величини вважається найбільш часто повторюване значення, або, як говорять, найбільш імовірне значення а, воно дорівнює середньому арифметичному з багатьох вимірювань
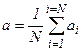, (1.1)
де N – число значень ai, отриманих з вимірювань. Абсолютні помилки окремих вимірювань a-a1=a1, a-a2=a2,…,a-ai=ai визначають абсолютну похибку величини a:
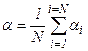. (1.2)
Остаточний результат вимірювання може бути записаний так: а ± a.
Абсолютна похибка має подвійний знак (±a) через те, що похибки рівної абсолютної величини і протилежних знаків рівноймовірнісні. Оскільки абсолютна похибка визначає інтервал, у якому знаходиться значення вимірюваної величини, то, як правило, воно містить одну значущу цифру, що, у свою чергу, визначає останню значущу цифру найбільш імовірної величини a. Наприклад, (22,4±0,5) см.
Погрішність прямих вимірювань обчислюється по формулі
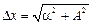, (1.3)
де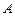 
— абсолютна погрішність засобу вимірювання (звичне це число рівне половині ціни розподілу вимірювального приладу або половині найменшого розряду індикатора).
У випадку, коли в результаті вимірювань отримано ряд однакових значень вимірюваної величини чи обчислена похибка менше тієї, що дасть прилад, то в якості середньої абсолютної похибки вибирається власна похибка приладу, зумовлена його класом точності чи рівна половині ціни найменшого поділку шкали приладу. Це ж правило стосується випадку, коли здійснюється тільки одне вимірювання.
У деяких окремих випадках середня похибка вимірюваної величини може бути менше похибки приладу. Наприклад, у тому випадку, якщо величина регулярно повторюється: коливання маятника, ціна поділу і т.д. При кількаразовому вимірюванні періоду коливання маятника Т =(2,0±0,2) сек. Однак, якщо вимірюється 100 коливань тим же секундоміром, то 100 Т =(200,0 ± 0,2) сек, або Т =(2,000 ± 0,002) сек.
1.1.3 Похибки непрямих вимірювань
Нижче наводяться теореми (без доказів), що дозволяють обчислити похибки побічно вимірюваних величин.
1 Абсолютна похибка суми дорівнює сумі абсолютних погрішностей доданків. Так, якщо X=а+b, де а і b - величини, які можна виміряти прямим методом з погрішністю ± ∆a і ± ∆b, то ∆Х=∆а+∆b, оскільки ∆а і ∆b мають подвійний знак, то при підсумовуванні ∆а і ∆b їхні знаки підбираються так, щоб ∆ Х було максимальним.
2 Абсолютна похибка різниці дорівнює сумі абсолютних погрішностей зменшуваного і від'ємника.
Нехай X=а-b, тоді ∆Х=∆а+∆b. Правило вибору знаків ∆а і ∆b те ж, що й у випадку 1. Слід зазначити, що це правило застосовне до усіх випадків обчислення погрішностей побічно вимірюваних величин.
3 Знайдемо абсолютну похибку добутку Х=аb. Нехай а±∆а, b±∆b, тоді ∆Х=а∆b+b∆а.
Абсолютна похибка дробу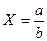 
(при а ± ∆ а і b ± ∆ b) дорівнює
.
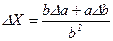З цих часткових теорем можна зробити висновок, що середні абсолютні похибки побічно вимірюваних величин знаходяться за правилами диференціювання формул, що зв'язують ці величини з тими, котрі вимірюють прямим шляхом. Необхідно тільки знак замінити знаком ∆ і вибрати знаки абсолютних погрішностей прямим шляхом вимірюваних величин так, щоб похибка непрямого вимірювання була максимальною. Слід зазначити, що після диференціювання вихідних залежностей і одержання формул погрішностей варто відкинути члени, утримуючі величини другого і більше порядку малості (тобто члени, утримуючі добутки ∆а∆b).
Відносна похибка непрямих вимірювань дорівнює
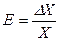. (1.4)
Однак, з іншого боку,
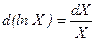або 
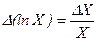. (1.5)
Отже, відносну похибку можна знайти логарифмуванням вихідного виразу і його наступного диференціювання із заміною знака a на знак ∆ і відповідним вибором знаків при абсолютних погрішностях прямих вимірювань.
По відносній похибці можна, надалі, знайти абсолютну похибку будь-якої складної залежності за допомогою простих формальних операцій. Наприклад, нехай
, 
,
,
.
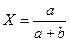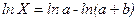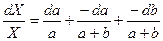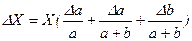Як бачимо, методом диференціального логарифма для знаходження абсолютних погрішностей користуватися зручніше і простіше, ніж методом простого диференціювання.
1.2 Елементи сучасної теорії погрішностей
При описі багатьох фізичних явищ неможливо прогнозувати точне поводження окремих фізичних подій. Однак їх можна описати, скориставшись поняттями "середнє поводження" чи "ймовірність".
Теорія ймовірностей основана на припущенні, що частота появи окремого результату в процесі експерименту наближається до кінцевої межі. Ймовірність Р(А) деякого результату А дорівнює частоті його появи
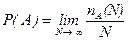, (1.6)
де N - загальне число дослідів чи спостережень; n(N) - число появ A під час цих дослідів.
У фізиці часто ймовірність можна визначити трохи інакше:
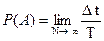, (1.7)
де ∆t - час спостереження результату A; Т - повний час експерименту.
Результат А (випадкова величина, тобто для її появи неможливо знайти причину чи причин занадто багато і їх вплив важко врахувати) може мати як дискретне значення, так і приймати нескінченно багато близьких значень (неперервний спектр). В останньому випадку характерна особливість: імовірність окремої події, що полягає в тому, що виникає саме результат А (певне значення) дорівнює нулю (близька до нуля). Тому можна говорити лише про ймовірність того, що випадкова величина може знаходитися в інтервалі ∆Х значень від Х до X+∆Х. Ймовірність d(X) того, що випадкова величина приймає значення від Х до X+dХ, залежить від самого Х, (тобто є деякою функцією f(X)) і від величини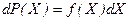 
.
Сукупність усіх значень ймовірностей даної величини утворює розподіл даної випадкової величини f(Х). Ця функція розподілу ймовірності показує, як розподіляється ймовірність на d в залежності від Х:
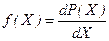, (1.8)
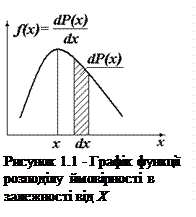і часто називається густиною ймовірності (рис.1.1). Звичайно f(X) виражається у вигляді графіка, з якого можна судити про величину dP(X) (площа заштрихованої ділянки).
Значення випадкової величини, що відповідає максимуму f(X), називається найімовірнішим.
В теорії ймовірностей і її додатків важливу роль відіграє диференціальний закон розподілу густини ймовірності випадкової величини, що має вигляд:
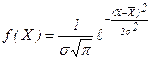
для дискретного ряду величин, де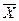 
- середнє значення чи математичне очікування
,
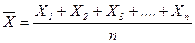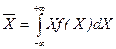- для випадкової величини, неперервно розподіленої (Х змінюється неперервно);
σ 2 - дисперсія випадкової величини.
Якщо
,
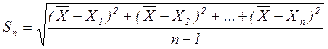тоді
.
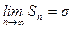Це середнє квадратичне відхилення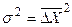 
називається дисперсією випадкової величини. Дисперсія визначає гостроту кривої f(Х). Форма кривих Гаусса (нормальний закон розподілу) представлена на рис.1.2 (для різних значень дисперсії).
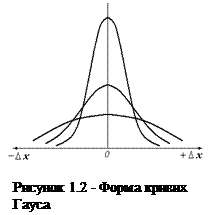При вимірюваннях фізичних величин у тих випадках, коли основну роль відіграють випадкові помилки, всі оцінки точності вимірювання можна зробити тільки з деякою ймовірністю. Для того, щоб виявити випадкову помилку вимірювань, їх необхідно повторити кілька разів. Якщо кожне вимірювання дає результати, трохи відмінні від інших, випадкова помилка відіграє істотну роль. За найбільш імовірне значення вимірюваної величини варто прийняти її середнє арифметичне значення за умови, що при великому числі вимірювань помилки однакової величини, але різного знака - рівноймовірнісні. Якщо помилки можуть приймати неперервний ряд значень і частота появ помилок зменшується зі збільшенням помилки при рівноточних (з однаковою старанністю проведених) вимірюваннях, то крива розподілу випадкових погрішностей описується кривою Гауса (нормальний закон розподілу випадкових величин):
,
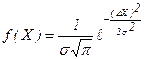де ∆X - величина випадкової похибки, ймовірність якої оцінюється f(X)=Y.
Отже, для характеристики похибки необхідно знати величину похибки ∆Х (∆Х називають довірчим інтервалом) і величину ймовірності того, що результат вимірювань характеризується даною погрішністю ∆Х (довірча імовірність або коефіцієнт надійності a). Вказівка однієї похибки без коефіцієнта надійності не має сенсу.
Для одержання чисельних результатів застосовуються таблиці нормального розподілу густини ймовірності, але щоб ними скористатися, необхідно нормувати f(X)
,
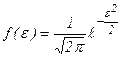де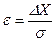 
- довірчий інтервал, виражений у частках середньої квадратичної помилки.
Нормована функція нормального розподілу імовірності
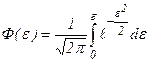
є функцією Лапласа (інтеграл ймовірностей). Так, наприклад, середній квадратичній помилці відповідає довірча імовірність 0,68 (=1), подвоєній середній квадратичній помилці (2 s) - довірча імовірність 0,95 (або 95 %) і т.д.
Часто, указуючи для оцінки похибки величину σ, не дають значення довірчої ймовірності, вважаючи її відомою величиною (68%).
Припустимо, вимірювана величина Z є сумою (чи різницею) Х і У, результати вимірювання яких незалежні,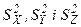 
- їхні дисперсії, тоді
.
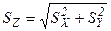Отже, для знаходження сумарної помилки потрібно складати не самі помилки, а їхні квадрати (SZ - середня квадратична помилка суми).
Нехай Х1, Х2, Х3..., Хn - результати окремих вимірювань, причому кожне з них характеризується однією і тією же дисперсією S. Середнє з них
.
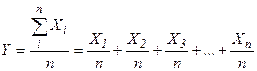Дисперсія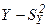 
,
.
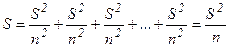Отже,
.
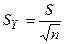Тоді середня квадратична похибка SY середнього арифметичного Y дорівнює середній квадратичній похибці окремого результату, поділеній на корінь квадратний з числа вимірювань. Тобто, збільшуючи кількість вимірювань, можна значно зменшити похибку, не покращуючи точність (зменшення S чи σ, що визначається методикою вимірювань). Нормальний закон розподілу випадкових погрішностей добре виконується при досить великій кількості вимірювань (кілька сотень) і дозволяє оцінити його параметри: σ2 для заданого ∆Х, чи ∆Х по заданому σ2.
Якщо ж число вимірювань невелике (менше двадцяти), то ці задачі можна вирішити, скориставшись іншим законом розподілу ймовірностей випадкових величин - розподілом Стьюдента:
,
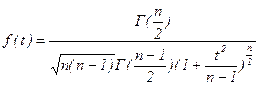де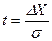 
;
∆X - абсолютна похибка результату серій вимірювання;
σ - середньоквадратична похибка результату тієї ж серії вимірювань;
Г(n) – гама функція.
При n →¥ (n →20) цей розподіл переходить у розподіл Гауса.
При малій серії вимірювань для розрахунку ∆Х при заданій надійності a використовують коефіцієнт Стьюдента ta, що залежить від кількості вимірювань n і величини a:
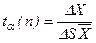, (1.9)
де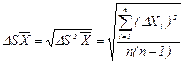 
- середньоквадратична похибка результату серій вимірювань.
Задаючи надійність, тобто припускаючи a рівним певній величині, за числом вимірювань n знаходимо в таблиці значення коефіцієнта Стьюдента. Визначивши ∆S 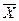, знаходимо ∆X:
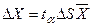. (1.10)
Результат можна записати у вигляді
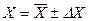. (1.11)
На закінчення пропонується зразковий порядок операцій для оцінки похибки прямих вимірювань.
1 Обчислюється середнє значення з n вимірювань:
.
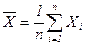2 Знаходяться похибки окремих вимірювань: 
.
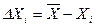3 Обчислюються квадрати погрішностей окремих вимірювань (∆Xi)2.
4 Якщо є вимірювання, що відрізняються різко за своїм значенням від інших, перевірити чи не є вони промахами.
5 Знаходять середню квадратичну похибку серії вимірювань
.
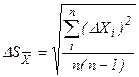6 Задається коефіцієнт надійності a.
7 Визначається коефіцієнт Стьюдента ta(n) для даного n і a за таблицею.
8 Знаходять межі довірчого інтервалу (похибка результату вимірювань)
.
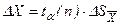9 Записується остаточний результат: .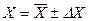
10 Визначається відносна похибка серії вимірювань - величина, що характеризує точність вимірювань
.
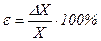1.3 Порядок виконання роботи
1. Отримати від викладача 3 екземпляри резисторів.
2. Ознайомитися з роботою мультиметра у режимі вимірювання опору. Навести значення абсолютних похибок.
3. Провести вимірювання опорів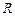 
резисторів. Вимірювання повторити 10 разів.
4. Ознайомитися з процесом вимірювання лінійних розмірів за допомогою штангенциркуля і мікрометра. Навести значення абсолютних похибок цих приладів.
5. Провести вимірювання геометричних параметрів резисторів: довжини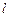 
, діаметру 
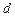. Вимірювання повторити 10 разів.
6. Визначити абсолютні і відносні похибки прямих вимірювань опору, довжини і діаметру резистора.
7. Навести формули для визначення похибки опосередкованих вимірювань наступних величин: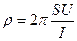 
, 
, 
, 
, 
, 
.
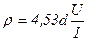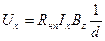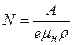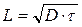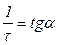8. Визначити похибку вимірювання питомого опору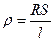 
1.4 Зміст звіту
Звіт повинен містити:
- короткі відомості з теорії похибок, визначення похибки прямих і опосередкованих вимірювань;
- таблицю проведених вимірювань величин 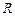, 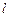і ;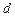
- обчислити похибки вимірювань, результати занести до таблиці;
- висновки.
1.5 Контрольні запитання
1. В чому полягає причини наявності похибок вимірювання?
2. Що таке промахи, систематичні і випадкові похибки.
3. Як знайти абсолютну похибку окремих вимірювань за великої і малої серії вимірювань?
4. Чому дорівнює абсолютна погрішність вимірювальних приладів?
5. Чому дорівнює погрішність прямих вимірювань?
6. Чому дорівнює погрішність опосередкованих вимірювань?
7. У чому полягає суть математичної обробки результатів досліду?
8. Що таке лінеаризація графіка?
Перелік рекомендованої літератури
1 Зельдович Я.Б., Мишкин Л.Д. Элементы прикладної математики. М.: "Наука", 1965.
2 Кортнев А.В., Рублев Б.В., Куценко А.Н. Практикум по физике.- М.: "Высш. школа", 1963.
3 Руководство к лабораторным занятиям по фізике /Под ред. Л.Л.Гольдина.- М.: "Наука", 1964.
4 Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и студентов ВУЗов.- М., 1959.
5 Демидович Б.П., Марон И.А. Основы вычислительной математики.- М., I960.
2 ЛАБОРАТОРНА РОБОТА №2 “ПЕРВИННА ОБРОБКА ЕКСПЕРИМЕНТАЛЬНИХ ДАНИХ. МАТЕМАТИЧНА ОБРОБКА РЕЗУЛЬТАТІВ ДОСЛІДУ”
Мета роботи:навчитися представляти результати експерименту у вигляді таблиць і графіків; підбір математичних формул.
2.1 Загальні відомості
Часто в результаті досліду зв'язок між деякими величинами виявляється у вигляді таблиці, у якій для кожного значення Х, при якому проводилось вимірювання (умови досліду), поставлене відповідне значення Y, знайдене шляхом вимірювань. Задані так функції можуть далі, наприклад, диференціюватися, інтегруватися, можуть знадобитися значення функції при проміжних, не вписаних у таблицю, значеннях незалежної змінної (задачі інтерполяції) чи при значеннях незалежної змінної, що знаходяться за межами таблиці (задача екстраполяції).
Для вирішення цих задач зручніше скористатися математичною залежністю між Х і Y, заданою у вигляді формули. Формулу, підібрану за експериментальними даними, називають емпіричною формулою. Формула тим ліпша, чим більше теоретичних уявлень вкладено в неї. Спочатку задаються видом формули, потім, скориставшись результатами сталих величин, що входять у формулу.
Перед тим, як приступити до підбора формули, необхідно нанести дослідні дані на графік, після чого на око, від руки провести через отримані точки найбільш правдоподібну криву. При цьому відразу виявляються ті дані, в яких можна підозрювати великі помилки. Дуже важливо при проведенні кривої, крім експериментальних точок, використовувати загальні розуміння про те, як повинна поводитися крива при значеннях аргументу, близьких до нуля, при дуже великих значеннях аргументу, поблизу початку координат, біля координатних осей (чи торкається їх, чи перетинає їх і т.п.).
Коли попередня робота проведена й обрано вид формули, можна визначити сталі коефіцієнти. Це роблять за допомогою методу найменших квадратів [1,2,5], однак він приводить до досить громіздких обчислень, особливо коли шукані параметри входять не лінійно. Тому в практичній роботі найчастіше більш ефективними виявляються графічні методи підбору формул.
Пряма лінія займає надзвичайний стан у графічному методі і надійно проводиться за даними точкам. Рівняння прямої лінії має вигляд:
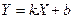, (1.12)
де числа k і b мають простий геометричний зміст: b - величина відрізка, що відтинається на осі Y, k - тангенс кута нахилу прямої до осі Х. Отже, побудувавши графік, ми визначимо b і k.
Велика перевага графічного методу зв'язана з його наочністю. Якщо експериментальні точки лягають на пряму, за винятком окремих точок, що випали, то ці точки наочно і можуть бути перевірені особливо ретельно. Якщо експериментальні точки не лежать на прямій, то це також видно з графіка. У цьому випадку залежність між Х і Y більш складна, ніж .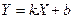
Як же підібрати константи, що входять у формулу, якщо вона має більш складний вид, ніж пряма?
Загальна ідея графічного методу полягає в тому, що треба ввести нові змінні так, щоб у цих змінних залежність, що нас цікавить, ставала лінійною. Тому метод іноді називають методом лінеаризації графіка чи просто методом вирівнювання.
Наприклад, часто зустрічається залежність виду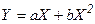 
.
Розділивши всі члени на Х:
,
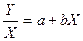і поклавши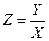 
, одержуємо лінійну залежність Z від Х. Або нехай 
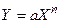. Логарифмуючи праву і ліву частини 
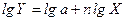, і ввівши нові змінні Z=lg і t=lg одержимо 
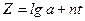. З графіка Z(t) легко знайдемо a і n.
Нехай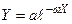 
. Логарифмуючи, одержимо 
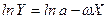, і вибираючи Z=ln, одержимо в координатах Z і Х пряму 
.
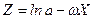В усіх цих прикладах ми після вибору виду формули вводили змінні так, щоб залежність між цими новими змінними була лінійною. Однак, якщо в нових змінних експериментальні точки не лягають на пряму, те це значить, що вид формули обраний невдало і для опису експериментальних даних треба підібрати формулу іншого виду.
Якщо немає теоретичних засад для підбора формули, звичайно вибирають функціональну залежність з числа найбільш простих, порівнюючи їхні графіки з графіками заданої функції. Через те, що подібність графіків визначена грубо, на око, потрібно, вибравши формулу, перш ніж визначати значення параметрів, перевірити можливість її застосування методом вирівнювання. Вказівки для вирівнювання найпростіших формул дані в [4].
Якщо емпіричну формулу відшукати не вдається, то часто бувають корисні операції безпосереднього графічного інтегрування, диференціювання, графічний розв`язок рівнянь та ін.
На закінчення необхідно відзначити, що при дослідженні багатьох технічних і наукових питань у даний час широке застосовується моделювання різних об'єктів чи явищ. У залежності від характеру дослідження моделювання може бути фізичним або математичним.
У випадку фізичного моделювання дослідження проводиться на моделі, фізично однорідної з об'єктом - оригіналом, що відрізняється від нього тільки кількісно. Таке моделювання дає можливість розширити відомості про явища, що відбуваються в оригіналі.
У випадку математичного моделювання дослідження виконується на моделі, що відтворює фізично інше явище, описуване, однак, такими ж рівняннями, як і явище в оригіналі. У цьому випадку моделюється не конкретний фізичний процес, а певна математична залежність. Цей вид моделювання є основою для створення різних обчислювальних пристроїв.
2.2 Порядок виконання роботи
1. Отримати у викладача вихідні дані.
2. Перенести дані у Excel.
3. Побудувати графік залежності.
4. Провести лінію тренда.
5. Лінеаризувати графік, знайти коефіцієнти a і b.
3 ЛАБОРАТОРНА РОБОТА №3 “РОБОТА З ОСЦИЛОГРАФОМ”
Мета роботи:навчитися працювати з осцилографом, провести вимірювання параметрів сигналу.
3.1 Загальні відомості
Осцилограф - прилад, який показує форму напруги в часі. Також він дозволяє вимірювати ряд параметрів сигналу, такі як напруга, струм, частота, кут зсуву фаз. Але головна користь від осцилографа - можливість спостереження форми сигналу. У багатьох випадках саме форма сигналу дозволяє визначити, що саме відбувається в ланцюзі. На рис. 3.1 показаний приклад подібної ситуації.
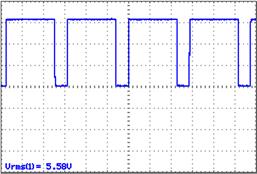
Рисунок 3.1 - Осцилограма складного сигналу
У цьому випадку напруга містить як постійну, так і змінну складові, причому форма змінної складової далека від синусоїдальної. На такому сигналі вольтметри дають велику похибку: стрілочний вольтметр змінного струму показав напругу 2,2 вольт, а цифровий - взагалі 1,99 вольт. Вольтметр постійного струму показав 4,8 вольт. Правильне діюче значення напруги показав осцилограф - 5,58 вольт (цифрові осцилографи вимірюють напругу і дозволяють зберігати результати в комп'ютерному форматі). Крім того, осциллограма дозволяє побачити деякі властивості сигналу:
- сигнал має імпульсний характер;
- сигнал не приймає негативних значень (виміряно з відкритим входом осцилографа);
- сигнал дуже швидко змінюється від нуля до значення 6,4 вольта і назад до нуля (чутливість каналу вертикального відхилення 2 В/под);
- тривалість імпульсів більш ніж у три рази перевищує тривалість пауз.
3.1.1 Принцип дії осцилографа
«Серцем» приладу є електронно-променева трубка (ЕПТ), рис. 3.2.
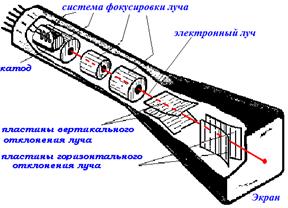
Рисунок 3.2 – Будова електронно-променевої трубки з електростатичним керуванням
ЕПТ є електронною лампою, і, як і всі лампи, вона «заповнена» вакуумом. Катод випромінює електрони, а система фокусування формує з них тонкий промінь. Цей електронний промінь потрапляє на екран, покритий люмінофором, який під впливом електронного бомбардування світиться, і в центрі екрану виникає точка, яка світиться. Дві пари пластин ЕПТ відхиляють електронний промінь у двох взаємно перпендикулярних напрямках, які можна розглядати як координатні осі. Тому для спостереження на екрані ЕПТ досліджуваної напруги необхідно, щоб промінь відхилявся по горизонтальній осі пропорційно часу, а по вертикальній осі - пропорційно досліджуваній напрузі.
На пластини горизонтального відхилення променя (розташовані вертикально) подається напруга розгортки. Вона має пилкоподібну форму: поступово лінійно наростає і швидко спадає. Негативна напруга відхиляє промінь вліво, а позитивна - вправо (якщо дивитися з боку екрану). В результаті промінь рухається по екрану зліва направо з певною постійною швидкістю, після чого дуже швидко повертається до лівої межі екрану і повторює свій рух. Відстань, яку проходить промінь уздовж горизонтальної осі, пропорційна часу. Цей процес називають розгорткою, а горизонтальну лінію, яку промінь прокреслює по екрану, називають лінією розгортки (іноді при вимірюваннях її називають нульовою лінією). Вона відіграє роль осі часу t графіка. Частоту повторення пилкоподібних імпульсів називають частотою розгортки, але її для вимірювань не використовують. Для вимірювань потрібно знати швидкість розгортки, про яку буде сказано нижче.
Якщо при цьому на пластини вертикального відхилення (розташовані горизонтально) подати досліджувану напругу, то промінь почне відхилятися і по вертикалі: при додатній напрузі вгору, а при від’ємній - униз. Рух по вертикалі і по горизонталі відбувається одночасно і в результаті досліджуваний сигнал «розгортається» в часі. Отримане зображення називають осцилограмою.
Насправді крім лінійної існує ще кругова і спіральна розгортки, а також фігури Ліссажу, коли один із сигналів є розгорткою для другого. Але це вже зовсім інша історія...
Важливим моментом є співвідношення частот розгортки і сигналу. Якщо ці частоти в точності рівні, то на екрані відображається рівно один період досліджуваного сигналу. Якщо частота сигналу вдвічі більше частоти розгортки, то ми побачимо два періоди, якщо втричі - то три. Якщо частота сигналу вдвічі менше частоти розгортки, то ми побачимо тільки половину періоду сигналу. Частоту (швидкість) розгортки можна регулювати в широких межах. Але зображення буде стабільним тільки в тому випадку, якщо частоти розгортки і сигналу точно збігаються. При найменшій розбіжності частот, кожний початок руху променя по екрану буде відповідати новій точці функції вхідного сигналу, і її графік щоразу буде малюватися в новому положенні. При невеликій розбіжності частот (частки герца) це буде виглядати як графік, який «пливе» ліворуч або праворуч. При розбіжності частот у кілька герц і більше, осцилограма стає такою, яку неможливо прочитати (рис. 3.3).
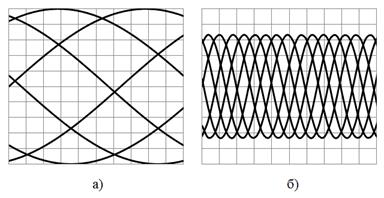
Рисунок 3.3 - Осцилограма за відсутності синхронізації
Домогтися абсолютно точного збігу частот (особливо в десятки-сотні кілогерц) практично неможливо. Тому розгорткою в осцилографі управляє спеціальна схема синхронізації. Вона затримує початок руху променя по екрану так, щоб промінь починав рухатися в той момент, коли вхідна напруга досягла певного значення. У цьому разі промінь починає рух (і рисування осцилограми) щоразу з однієї і тієї самої точки графіка вхідного сигналу. У результаті кожен наступний рух променя рисує картинку в одному і тому самому положенні, навіть якщо частоти сигналу і розгортки помітно не збігаються. Зображення виходить стабільним і стійким. Напруга сигналу, при якій відбувається синхронізація (рівень синхронізації), задається органами управління осцилографа. Візуально зміна цієї напруги викликає зсув початку зображуваного графіка відносно початку періоду сигналу, рис. 3.4.
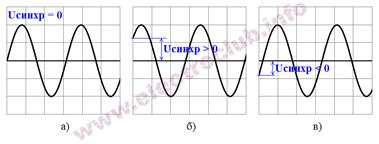
Рисунок 3.4 - Осцилограми при різних рівнях синхронізації
Для спостереження кількох сигналів одночасно випускають багатопроменеві і багатоканальні осцилографи. Звичайно кількість каналів дорівнює двом (інакше виходить дуже складно і дорого). ЕПТ двопроменевих осцилографів працює одночасно з двома променями на загальному екрані, які дозволяють спостерігати два сигнали абсолютно незалежно. Але такі прилади складні і дорогі. Тому більш поширені двоканальні осцилографи. Їх ЕПТ звичайна, але вони мають два окремі входи і два незалежних підсилювача вертикального відхилення, які обслуговують вхідні сигнали. Крім того, вони мають вбудований високошвидкісний комутатор, який дуже швидко перемикає ЕПТ (пластини вертикального відхилення) від одного каналу до іншого. Зображення сигналів при цьому не є безперервними лініями, а складаються з безлічі штрихів. Але на екрані штрихи зливаються, і в результаті виходить два графіка вхідних сигналів. Лише при спостереженні високочастотних сигналів і невдалій частоті розгортки зображення може стати пунктирним.
Підключення осцилографа
Оскільки напруга вимірюється між двома точками, то вхід осцилографа має дві клеми. Причому вони не рівнозначні. Одна клема, так звана «фаза», підключена до входу підсилювача вертикального відхилення променя. Друга клема - «земля» або «корпус». Вона називається так тому, що електрично з'єднана з корпусом приладу (це загальна точка всіх його електронних схем). Осцилограф показує напругу фази по відношенню до землі.
Дуже важливо знати, який з вхідних провідників є фазою. Для визначення який з провідників є фазою, а який корпусом, треба при нікуди не підключеному осцилографі взятися рукою за контакт одного з вхідних провідників, при цьому іншою рукою ні до чого не торкатися. Якщо цей провідник - корпус, то на екрані буде тільки лише горизонтальна лінія розгортки. Якщо цей провідник - фаза, то на екрані виникнуть досить значні завади, які представляють собою сильно спотворену синусоїду частотою 50 Гц.
Визначивши фазу і корпус вхідного кабелю, можна підключати осцилограф до досліджуваного ланцюга. Якщо в ньому немає чітко вираженого загального проводу, то корпус підключається до будь-якої з точок, напругу між якими потрібно дослідити. Якщо в ланцюзі є загальний провід - точка, яку умовно приймають за нульовий потенціал, поєднана з корпусом пристрою або реально заземлена, то корпус осцилографа краще підключати до цієї точки. Невиконання цього правила може призвести до значних похибок вимірювань (іноді настільки великих, що вимірюванням і зовсім не можна довіряти).
За своєю суттю осцилограф є вольтметром, який показує графік напруги. Проте з його допомогою можна спостерігати і форму струму. Для цього послідовно з досліджуваним ланцюгом включають резистор R с (тут індекс «с» означає струмовий), рис. 3.5. Опір резистора R с вибирають набагато меншим, ніж опір ланцюга, тоді резистор не впливає на його роботу і його включення не призводить до змін режиму роботи ланцюга. На резисторі за законом Ома виникає напруга:
.
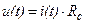Цю напругу і вимірюють осцилографом. А знаючи величину R с, можна перевести напругу, яку показує осцилограф, у струм.
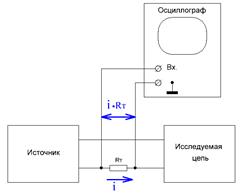
Рисунок 3.5 – Вимірювання струму осцилографом
Двоканальний (і двопроменевий) осцилограф може показувати осцилограми двох сигналів одночасно. Для цього у нього є два входи (канали), які зазвичай позначаються I і II. Слід пам'ятати, що одна з вхідних клем кожного каналу з'єднана з корпусом осцилографа, отже, клеми «корпус» обох каналів з'єднані між собою. Тому ці клеми повинні підключатися до однієї і тієї самої точки ланцюга, інакше в ланцюзі виникне замикання.
Можливість спостерігати не будь-які дві напруги, а тільки ті, які мають спільну точку, є недоліком, але невеликим - в електроніці один з полюсів джерела живлення завжди є загальним проводом, і всі напруги вимірюються відносно нього.
Використовуючи двоканальний осцилограф можна одночасно спостерігати і напругу, і струм в ланцюзі і, отже, вимірювати зсув фаз між струмом і напругою. Схему підключення осцилографа в цьому випадку показано на рис. 3.6.
Канал І вимірює напругу, а канал II вимірює струм. Таке включення найбільш оптимальне, оскільки напруга, яка падає на резисторі R с і подається в канал II, у 30... 100 разів менше, ніж у каналі І, отже, воно більше піддається завадам і синхронізація від низької напруги не така добра. Крім того, конструкція більшості осцилографів трохи «несиметрична» - синхронізація від сигналу каналу І зазвичай більш якісна і стабільна. Отже, підключення каналу І до напруги забезпечує більш стабільне зображення осцилограми.
Помилка підключення на рис. 3.6, б полягає в тому, що клеми корпусу обох входів не з'єднані одній точці. В результаті резистор R с виявляється замкнутий накоротко через корпус осцилографа. Найнеприємніше, що при цьому напруга на резисторі R с не дорівнює нулю - через те, що опір проводів вхідних кабелів (через які цей резистор замикається) не нульовий. Тому при такому підключенні можна не помітити цю помилку (адже осцилограф щось показує), а результат вимірювання струму при цьому буде невірним.
Включення, показане на рис. 3.6, в невдале в тому, що канал І осцилографа вимірює не напругу в досліджуваному ланцюзі, а суму напруг в ланцюзі і на резисторі R с (напруга вимірюється не на навантаженні, а на джерелі). Напруга на R с хоч і невелика за величиною, але все одно вносить похибки у вимірювання напруги.
Підключення осцилографа, показане на рис.11а, не тільки забезпечує найбільшу точність вимірювань, але й дозволяє в ряді випадків використовувати резистор R с з досить великим опором. Це важливо при вимірюванні малих струмів: якщо і струм в ланцюзі і опір R с малі, то напруга, яка виникає на R с, може бути настільки маленькою, що чутливості осцилографа не вистачить для її відображення.
При вимірюванні зсуву фаз необхідно інвертувати сигнал у каналі II, оскільки канал II включений зустрічно по відношенню до каналу I.
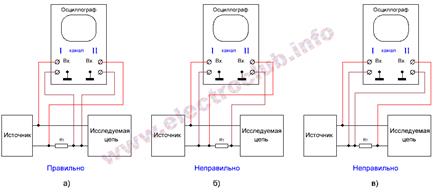
Рисунок 3.6 - Підключення осцилографа для вимірювання зсуву фаз
А – управління каналом I; Б – управління відображенням каналів;
В – управління каналом II; Г – регулювання яскравості променя,
фокусування і підсвічування екрану; Д – управління розгорткою; Е – управління синхронізацією
Рисунок 3.7 - Передня панель осцилографа С1-83
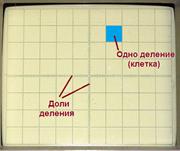Рисунок 3.8 – Поділки екрану осцилографа
| 
Рисунок 3.9 - Органи управління каналу I
|
3.1.3 Управління осцилографом
Розглянемо передню панель двоканального осцилографа С1-83 (рис. 3.7). Добре видно, що екран осцилографа розбитий на клітини (рис. 3.8). Ці клітини називаються поділками, і використовуються при вимірюваннях: до них прив'язуються всі масштаби по вертикалі і горизонталі. Масштаб по вертикалі - вольти на поділку (В/под. або V/под.), масштаб по горизонталі секунди (мілі- та мікросекунди) на поділку. Зазвичай осцилограф має 6...10 поділок по горизонталі і 4...8 поділок по вертикалі. Центральні вертикальна і горизонтальна лінії мають додаткові риски, які ділять поділку на 5 або 10 частин (рис. 13, на рис. 12 теж видно). Риски служать для більш точних вимірювань, вони є частками поділки.
Управління обома каналами однакове. Розглянемо його на прикладі каналу I (рис. 3.9).
1. Перемикач режиму входу. У верхньому положенні «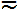
» на вхід надходить і постійна і змінна напруги. Це називають «відкритий вхід» - тобто відкритий для постійного струму. У нижньому положенні «~» на вхід проходить тільки змінна напруга, що дозволяє вимірювати маленьку змінну напругу на тлі великого постійного, наприклад в підсилювачах. Реалізується це дуже просто: вхід підсилювача підключається через конденсатор. Це називають «закритий вхід». Майте на увазі, що при закритому вході дуже низькі частоти (нижче 1...5 Гц) значно послаблюються, тому вимірювати їх можна тільки при відкритому вході. У середньому положенні перемикача 1 вхід підсилювача осцилографа відключається від вхідного роз'єму і замикається на землю. Це дозволяє за допомогою ручки 7 виставити лінію розгортки в потрібне місце.
Вхідний роз'єм каналу
3, 4, 5, 6 - регулятор чутливості каналу вертикального відхилення (масштабу по вертикалі). Перемикач 4 задає масштаб східчасто. Значення, які він задає, нанесені поруч з ним. На вибране значення вказує риска 5 на перемикачі. На рисунку вона вказує на значення 0,2 вольта/поділку. Ручка 3, розміщена співвісно з перемикачем, дозволяє плавно зменшувати масштаб у 2...3 рази. У крайньому правому положенні (на рис. 14 ручка «плавно» знаходиться саме в ньому) ця ручка має фіксацію, тоді масштаб по вертикалі в точності дорівнює заданому перемикачем 4. Значення масштабів, виділені дужкою 6, вказані в мілівольтах на поділку - про це говорить напис «мВ» всередині дужки.
Ручка 7 виконує дві функції. При обертанні вона переміщує графік каналу по вертикалі вгору або вниз ↕. При «витягуванні» задає множник масштабу по вертикалі: витягнута ручка (рис. 3.10) задає множник х1, а втоплена - множник х10. Втоплене і витягнуте положення символічно показані над і під ручкою.
Канал II аналогічний каналу I. Але другий канал має додатковий перемикач 6, що дозволяє інвертувати його вхідний сигнал. У натиснутому положенні канал працює як звичайно, а у витягнутому - інвертується, тобто при негативному вхідному сигналі промінь рухається вгору, а при позитивному - вниз. Це необхідно при вимірюванні, наприклад, зсуву фаз.
Рисунок 3.10 - Ручка множника масштаба по вертикалі, витягнута в положення «х1»
| 
Рисунок 3.11 - Управління відображенням каналів
|
На рис. 3.11 показано управління відображенням каналів, яке визначається натисканням на одну з кнопок.
1 - Працює тільки канал I, II канал відключений.
2 - Обидва канали відображаються одночасно (промінь дуже швидко переключається між каналами) і взаємне положення осцилограм обох каналів вірне. У цьому режимі можна вимірювати зсув фаз.
3 - Осцилограф показує суму або різницю сигналів в каналах (знак другого каналу визначається положенням ручки 6 на другому каналі).
4 - Відображаються сигнали обох каналів, але вони незалежні в часі, тому порівнювати сигнали відносно часу і зсуву фаз не можна.
5 - Працює тільки канал II, канал І відключений.
Панель управління розгорткою (рис. 3.12) схожа на панель управління каналом вертикального відхилення променя. Вона містить ручку 4, яка дозволяє зсувати зображення вліво-вправо «↔» і комбінований регулятор (1 - східчасто, 3 - плавно) швидкості розгортки (масштабу по горизонталі). Риска 2 на перемикачі показує встановлене значення. Як і в каналах вертикального відхилення, перемикач швидкості розгортки має різні одиниці вимірювання: секунди с, мілісекунди мс, мікросекунди мкс. Витягнута/втоплена ручка 4 «↔» задає множник швидкості розгортки відповідно х0,2 і х1. Зверніть увагу: на рис. 3.12 ручка 3 регулювання швидкості розгортки «плавно» встановлена не в крайнє праве положення. Отже, швидкість розгортки не дорівнює значенню, заданому перемикачем 1, а менше нього (швидкість руху променя менше, а значення час / поділка більше!).
Рисунок 3.12 - Органи управління розгорткою
| 
Рисунок 3.13 - Органи управління синхронізацією
|
На панелі управління синхронізацією (рис. 3.13) задається:
1 - джерело внутрішньої синхронізації: напругою якого каналу синхронізується рух променя. Ця синхронізація проводиться вхідним сигналом, тому називається внутрішньою. Такий режим використовується для більшості вимірювань. Варіанти тут такі: або синхронізація тільки сигналом каналу I, або спроба синхронізації від каналу I, а якщо не виходить, то синхронізація проводиться сигналом каналу II. Перший варіант іноді працює трохи краще, тому треба намагатися, щоб сигнал першого каналу був досить великий для стабільної синхронізації. У переважній більшості випадків для нормальної роботи слід вибирати саме цей режим синхронізації, включивши кнопку «I».
2 - зовнішня синхронізація. Рух променя синхронізується імпульсами, поданими зі спеціального зовнішнього джерела на вхід синхронізації осцилографа. Такий режим іноді потрібний для дослідження специфічних сигналів. Якщо зовнішнього джерела синхронізації немає, то отримати стійке зображення неможливо. Кнопки «0,5-5» і «5-50» задають діапазон вхідних напруг від зовнішнього джерела синхронізації. Кнопка «X-Y» спільно з кнопкою «II X-Y» управління відображенням каналів подає сигнал каналу II на пластини горизонтальної розгортки. У цьому режимі можна спостерігати фігури Ліссажу.
3 - ручка «Рівень синхронізації» - задає напругу синхронізації. У натиснутому положенні цієї ручки (як на рисунку) розгортка автоматична. При цьому промінь рухатиметься навіть якщо синхронізації не відбудеться. Промінь затримується на початку руху на деякий час до моменту синхронізації, але через деякий час все одно починає рух. Це «м'який» режим, більш зручний для роботи, оскільки промінь завжди залишається видимим. У витягнутому положенні ручки включається чекаюча розгортка. У цьому режимі промінь не почне руху до тих пір, поки не відбудеться синхронізації. Якщо синхронізації не відбувається, промінь не рухається. Такий режим добре підходить для спостереження неперіодичних сигналів. Вплив цієї ручки на зображення показаний на рис. 3.3 і 3.4.
4 - «полярність» синхронізації. Насправді знаки «+» і «-» означають дещо інше. У положенні «+» синхронізація відбувається по фронту, тобто в той момент, коли вхідна напруга досягає заданого (ручкою «Рівень синхронізації») значення при наростанні вхідної напруги (зміні від «-» до «+»). У положенні «-» синхронізація відбувається по спаду - при убуванні вхідної напруги (зміні від «+» до «-»). В осцилографі в ланцюзі синхронізації використовують дві різні схеми: одна визначає чи дорівнює вхідна напруга заданій і якщо дорівнює - запускає рух променя. Ця напруга задається ручкою «Рівень синхронізації». Друга схема визначає, як при цьому змінюється вхідна напруга - зростає або убуває. І відповідно дозволяє першій схемі спрацювати.
Режим входу синхронізації. Відноситься як до зовнішньої, так і до внутрішньої синхронізації. У положенні «~» вхід закритий, і синхронізація відбувається тільки від змінної напруги. У положенні «» вхід відкритий, і на спрацьовування схеми синхронізації діє і змінна напруга, і постійна. Режим «НЧ» те ж саме, але сигнал потрапляє на ланцюг синхронізації через фільтр низьких частот, який обрізає високочастотні завади. Цей режим є не у всіх осцилографах.
