Нестационарные аэродинамические характеристики треугольного крыла
В настоящем разделе рассматриваются результаты для нестационарных аэродинамических производных и полных зависимостей аэродинамических характеристик треугольного крыла при неустановившемся движении.
Экспериментальные исследования были проведены на модели треугольного крыла удлинением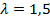 
. Модель крыла выполнена в виде пластинки с толщиной 
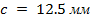, что составляет около 1.2% корневой хорды, со скруглёнными передними и заостренной задней кромкой и имеет следующие основные параметры: размах 
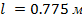, корневую хорду 
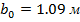, САХ 
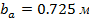, площадь 
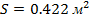. Угол стреловидности крыла по передней кромке 
.
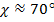Исследования проводились в аэродинамической трубе Т-103 ЦАГИ при скорости потока 
, что соответствует числу Рейнольдса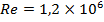 
рассчитанному по САХ крыла. Центр колебаний модели располагался в точке 
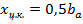. Относительно этой же точки проводились измерения аэродинамических моментов.
Влияние частоты колебаний на нестационарные аэродинамические производные
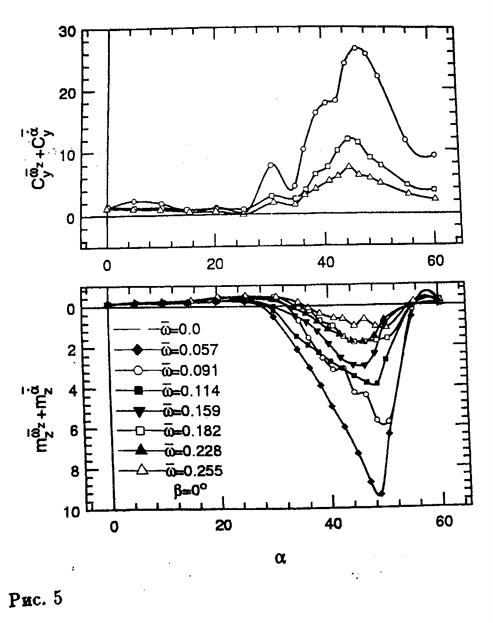
Нестационарные аэродинамические производные крыла исследовались при колебаниях с малой амплитудой (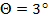
). На рис. 5 приведены результаты обработки эксперимента при колебаниях по тангажу треугольного крыла с различными частотами. Показаны полученные зависимости от угла атаки производных продольной силы и момента в фазе с изменением угла атаки - динамические производные 
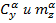, а также производные в фазе с 
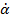- комплексы вращательных и нестационарных производных 
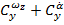и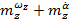 
. Начиная с угла атаки 
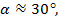вихри начинают разрушаться, что приводит к быстрому уменьшению несущих свойств. На этих же углах атаки нестационарные аэродинамические производные начинают зависеть от частоты колебаний модели в потоке, см. рис. 5. Сплошными символами обозначены экспериментальные результаты, приведенные в работе [1]. При этом использовалась та же модель крыла и та же установка, что и в настоящей работе. Амплитуда колебаний также составляла 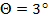. Однако, испытания проводились при другой скорости набегающего потока 
, вследствие чего приведенные безразмерные частоты колебаний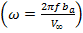 
различаются. Эти экспериментальные результаты обрабатывались по другой методике с использованием БПФ. Видно, что на малых углах атаки, когда разрушение вихрей происходит в следе, за крылом и на больших углах атаки, когда вихревая система крыла полностью разрушена, эти данные совпадают с производными, полученными в настоящей работе, а в области, где нестационарные производные зависят от частоты, они дополняют результаты настоящего исследования.
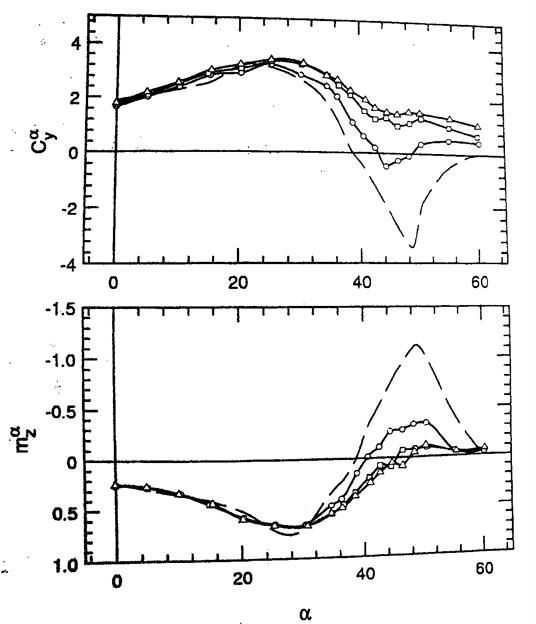
На графиках производных 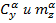пунктирными линиями показаны соответствующие зависимости, полученные по результатам эксперимента в стационарных условиях. Данные нестационарных экспериментов с различными частотами существенно отличаются от статических результатов также только в диапазоне углов атаки динамического разрушения вихрей.
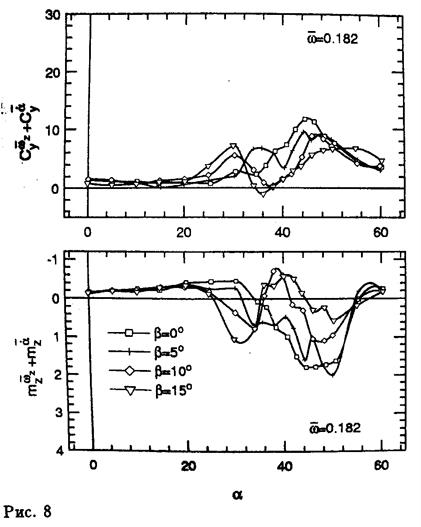
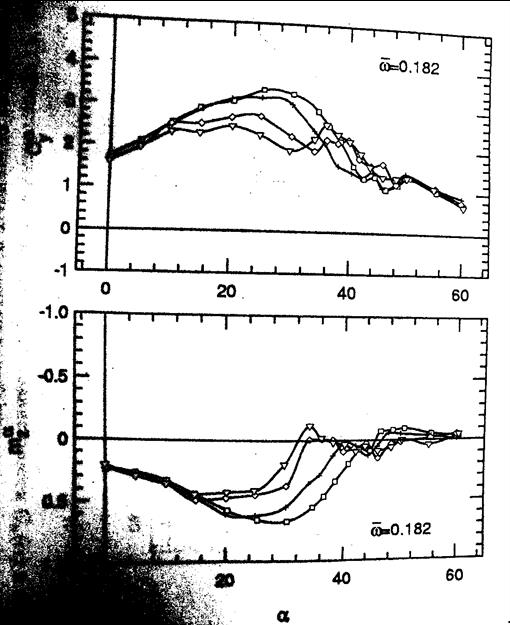
На рис. 6 показаны аналогичные экспериментальные результаты, полученные при колебаниях модели по крену с различными частотами. Видно, что, также как и при колебаниях по тангажу, производная момента крена в фазе с изменением угла крена -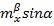 
и комплекс вращательных и нестационарных производных - 
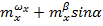зависят от частоты колебаний только в диапазоне углов атаки 
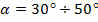, что соответствует разрушению вихрей над крылом.
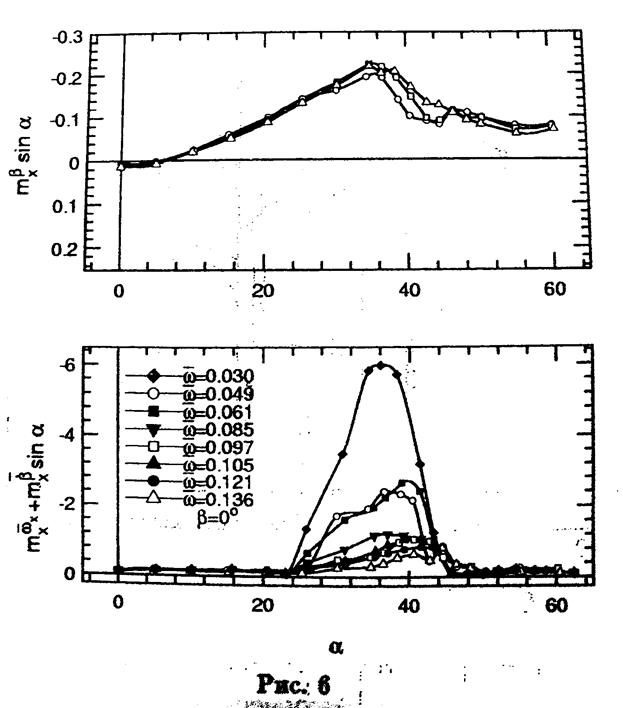
При меньших углах атаки вихри разрушаются в следе за задней кромкой, при больших - вихри полностью разрушены. Сплошными символами обозначены экспериментальные результаты, приведённые в работе [1]. Кроме получения нестационарных аэродинамических производных при вынужденных колебаниях с. малой амплитудой относительно различных осей, данные эксперимента были также обработаны сцелью получения полных динамических зависимостей аэродинамических сил и моментов при таких колебаниях.
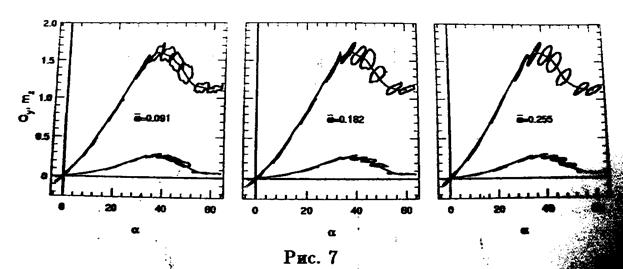
На рис. 7 показаны соответствующие результаты обработки при колебаниях в плоскости тангажа с различными частотами. Видно значительное отличие статических зависимостей Су (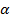
) и mz(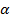) от их динамических значений в диапазоне углов атаки 
.
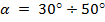