У процесі перевірки повторюють усі обчислення, виконані в полі. В даному прикладі заново обчислюють значення кутів з окремих напівприйомів (КЛ і КП), знаходять їх середнє значення, обчислюють значення місця нуля (МО) вертикального круга, знаходять значення кутів нахилу сторін, обчислюють середні значення довжин сторін, виміряних у першому і другому півприйомах в прямому та оберненому напрямах. Обчислюють
горизонтальні прокладення сторін ходу в прямому та оберненому напрямах та їх середнє значення. Визначають перевищення в прямому та оберненому напрямах та їх середнє значення.
Середні значення виміряних горизонтальних кутів, кутів нахилу, та обчислені значеня місця нуля, довжин сторін, горизонтального прокладання та перевищення записують в колонки 5, 9, 11-13 табл. 4.1 і підкреслюють або записують іншим кольором.
Виконаємо вище перераховані обчислення для вимірювань, які виконані на станції 2 тахеометричного ходу (див. табл. 4.1.).
а).Обчислення середнього значення горизонтального кута з двох пів прийомів.
З табл. 4.1. беремо значення відліків по горизонтальному кругу по початковій точці (Вп) та кінцевій точці (Вк) при положеннях вертикального круга КЛ (вліво) і КП (вправо). (колонка 4, табл. 4.1.)
При положені вертикального круга:
КЛ Вп= 0°02,5'; Вк=359°29,0'; βл = 359°29,0'- 0°02,5'=359°26,5'
КП Вп=181° 32,5'; Вк=180° 59,0'; βп=180° 59,0'-181° 32,5'+ 360°=359°26,5'
βср= 
= 
Записуємо обчислені значення кутів βл, βп, βср в колонку 5 табл. 4.1
в такому порядку: вверх – βл, по середині – βср і внизу – βп.
βл
βср
Примітка 1.При визначенні кута βп ми отримуємо його значення від'ємним, тому додається 360°
2. Розбіжність значень βл і βп не повинна перевищувати 1'.
б). Обчислення місця нуля і кута нахилу.
Для визначення кутів беремо відліки по вертикальному кругу при його положеннях: КЛ і КП (колонка 8, табл.4.1) та за формулами визначаємо
МО і δ.
МО = 
= 
δ=Л-МО=-3°01,5'-0=-3°01,5'
Записуємо отримані значення МО і δ в колонку 9 табл. 4.1 в такому порядку:
.
Примітка. Розбіжність відліків вертикального круга Л і П не повинна перевищувати 1'.
в). Обчислення середнього значення довжини сторони виміряних у першому і другому півприйомах, та в прямому і оберненому напрямах.
Беремо віддалемірні відліки по рейці (колонка 10 табл. 4.1) які виміряні при положеннях вертикального круга КЛ і КП. (сторона ходу 2 
3).
Dл = 178,0; Dп = 178,0; Dср =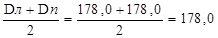 
м.
Це визначення середньої довжини сторони рахується прямим.
Коли вимірювання будуть проводитися на пункті ходу 3, то знову у двох півприйомах буде визначатися довжина цієї ж сторони тільки в напрямку 3 2. Обчислення виконуються аналогічно, а визначене значення рахується оберненим. Визначені середні значення довжини сторони ходу записуються в колонку 11 табл.4.1
Примітки: 1. Розбіжність між результатами вимірювань, отриманих у першому і другому півприйомах не повинна перевищувати 
.
2. Розбіжність між результатами вимірювань сторони ходу в прямому та зворотному напрямках не повинна перевищувати 
.
г).Обчислення горизонтального прокладання.
Для визначення горизонтального прокладення використовується формула
d = D · cos² δ
де d – горизонтальне прокладення;
D – віддаль, яка визначається за допомогою ниткового віддалеміру;
δ – кут нахилу.
Горизонтальне прокладення визначається пряме, обернене та середнє.
Прямим горизонтальним прокладенням є прокладення визначене за значенням сторони ходу яке рахується прямим і оберненим за значенням сторони ходу яке рахується оберненим. Наприклад: довжина сторони ходу за напрямком 2 3 – пряма, а за напрямком 3 2 - обернена.
Середнє значення визначається з виразу
dср = 
Наприклад, для напряму 2-3 (прямий напрям) середня віддаль з двух
півприйомів Dпр =178,0м, а для оберненого напряму 3-2, Dоб=177,0м. Тоді горизонтальні прокладення визначаються таким чином:
dпр=Dпр· cos² δ=178,0 · cos²(-3°01,5')=177,5м
dоб=Dоб· cos² δ=177,0 · cos²(-3°01,5')=176,5м
Розбіжність цих значень 
> .
На практиці це означає, що віддаль визначена не точно, не задовольняє вимоги до точності і її необхідно визначити повторно.
З навчальною метою продовжуємо обчислення,
dср = 
м.
Визначені таким чином значення dпр, dоб, dср заносяться в колонку 12 табл. 4.1 в такому порядку:
dпр
dср
dоб
Примітки: 1. Розбіжність значень горизонтального прокладення в прямому і оберненому напрямах не повинна перевищувати .
2.При значеннях кутів нахилу ліній, що не перевищують 1,5°, горизонтальне прокладення ліній можна приймати рівним довжині сторони ходу.
г).Обчислення перевищення: прямого, оберненого та середнього.
(h пр, h об, h ср).
Розрахунки виконуються за загальною формулою:
h = d · tg δ + і - v, а при і = v, h = d · tg δ.
h пр = dпр · tg δ; h об= dоб · tg δ; h ср= 
.
Для нашого прикладу:
h пр = dпр · tg δ=177,5· tg (-3°01,5')= - 9,38м.
h об = dоб · tg δ=176,5· tg (+3°01,5')= +9,32м.
Розбіжність значень перевищень h пр- h об = - 9,38 – (+9,32) = - 6см.
Допустима розбіжність 4см на 100м. Отримана різниця в прикладі допустима. Якщо різниця перевищень більша встановленого допуску, то вимірювання необхідно повторити.
h ср= 
= - 9,35м.
При обчисленні h ср знак оберненого перевищення міняємо на протилежний.
Отримані результати заносимо в колонку 13 табл.4.1 в такому порядку:
h пр
h ср
h об
Повністю опрацьований журнал вимірювань у тахеометричному ході має вид (див.табл.4.1а)
