З а д а ч а № 1
Сталевий брус (рис.3.1, питома вага сталі 
, модуль пружності 
) знаходиться під дією поздовжньої сили F і власної ваги.
Потрібно:
1. Побудувати епюру поздовжніх сил.
2. Побудувати епюру нормальних напруг.
3. Визначити переміщення перерізу І-І.
Дані взяти із таблиці 3.1.
Л і т е р а т у р а: [ I ] §15, 36; [ 2 ] §1.14; [ 3 ] §24; [ 4 ] §7.2
Таблиця 3.1 (дані до задач 1; 2)
| Букви алфавіту | Схема | А, 10-4 м2 | а | b | с | F, кН |
| м | ||||||
| А | 1,10 | 1,15 | 1,20 | 1,10 | ||
| Б | 1,15 | 1,20 | 1,25 | 1,15 | ||
| В | 1,20 | 1,25 | 1,30 | 1,20 | ||
| Г | 1,25 | 1,30 | 1,35 | 1,25 | ||
| Д | 1,30 | 1,35 | 1,40 | 1,35 | ||
| Е | 1,35 | 1,40 | 1,45 | 1,40 | ||
| Є | 1,40 | 1,45 | 1,50 | 1,45 | ||
| Ж | 1,45 | 1,50 | 1,55 | 1,50 | ||
| З | 1,50 | 1,55 | 1,60 | 1,60 | ||
| И | 1,55 | 1,60 | 1,65 | 1,70 | ||
| І, Ї | 1,60 | 1,65 | 1,70 | 1,80 | ||
| Й | 1,65 | 1,70 | 1,75 | 1,90 | ||
| К | 1,70 | 1,75 | 1,80 | 2,00 | ||
| Л | 1,75 | 1,80 | 1,85 | 1,90 | ||
| М | 1,80 | 1,85 | 1,90 | 1,80 | ||
| Н | 1,85 | 1,90 | 1,95 | 1,70 | ||
| О | 1,90 | 1,95 | 2,00 | 1,60 | ||
| П | 1,70 | 1,80 | 1,90 | 1,50 | ||
| Р | 1,60 | 1,70 | 1,80 | 1,40 | ||
| С | 1,55 | 1,65 | 1,75 | 1,30 | ||
| Т | 1,35 | 1,45 | 1,55 | 1,20 | ||
| У | 1,25 | 1,35 | 1,45 | 1,10 | ||
| Ф | 1,15 | 1,25 | 1,35 | 1,15 | ||
| Х | 1,10 | 1,20 | 1,30 | 1,25 | ||
| Ц | 1,05 | 1,15 | 1,25 | 1,35 | ||
| Ч | 1,25 | 1,35 | 1,45 | 1,45 | ||
| Ш | 1,45 | 1,55 | 1,65 | 1,55 | ||
| Щ | 1,65 | 1,75 | 1,85 | 1,65 | ||
| Ю | 1,75 | 1,85 | 1,95 | 1,75 | ||
| Я | 1,80 | 1,90 | 2,00 | 1,80 | ||
| Ь | 2,00 | 2,00 | 2,20 | 1,90 |
Рис 3.1. Схема бруса
З а д а ч а № 2
Абсолютно жорсткий брус спирається на шарнірно-нерухому опору і прикріплений до двох стержнів за допомогою шарнірів (рис.3.2).
Потрібно:
1. Знайти зусилля і напруги в стержнях, виразивши їх через силу Q.
2. Знайти допустиме навантаження Qadm. Більшу із напруг в двох стержнях прирівняти до допустимої напруги 
= 160 МПа.
3. Знайти граничну вантажопідйомність системи Qи і допустиме навантаження Qadm, якщо границя текучості 
= 240 МПа і запас міцності n = 1,5.
4. Порівняти величини Qadm, які були одержані при розрахунках за допустимою напругою (п.2) і допустимим навантаженням (п.3).
Рис.3.2. Схема закріплення жорсткого бруса
Дані взяти із таблиці 3.1 і рис. 3.2.
В к а з і в к а. Для визначення двох невідомих зусиль в стержнях потрібно скласти одне рівняння рівноваги і одне рівняння сумісності деформацій.
Для відповіді на третє питання потрібно мати на увазі, що в одному із стержнів напруга буде більшою ніж в другому; умовно назвемо цей стержень першим. При збільшенні навантаження напруга в першому стержні досягне границі текучості раніше ніж у другому. Коли це відбудеться, напруга в першому стержні деякий час не буде зростати, якщо навантаження буде зростати. Система, таким чином, стає статично визначною, навантаженою силою Q ( поки що невідомою) і зусиллям в першому стержні:
(С)
При подальшому збільшенні навантаження напруга і в другому стержні досягне границі текучості:
(Д)
Складемо рівняння рівноваги і підставляємо в нього значення зусиль (С) і (Д). З одержаного рівняння визначаємо граничну вантажопідйомність Qи.
Л і т е р а т у р а: [ I ] §15, 36, 37; [ 2 ] §1.14-15; [ 3 ] §18, 24; [ 4 ] §7.2; 9.2.
З а д а ч а № 3
Для заданого сталевого вала трубчастого поперечного перерізу (рис. 3.3) потрібно:
1. Визначити величину моменту Те 5 з умови рівноваги вала.
2. Побудувати епюру крутних моментів.
3. Визначити зовнішній і внутрішній діаметри вала, виходячи з умови міцності. Відношення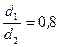 
. Одержані розміри округлити до 5 мм. Наприклад: d = 30, 35, 40, 45, 50 і т.д.
4. Визначити кут закручування вала на кожній ділянці; модуль пружності зсуву для сталі 
.
5. Побудувати епюру кутів закручування вала.
6. Визначити найбільший відносний кут закручування вала (на 1 пог. м).
Рис. 3.3. Розрахункова схема вала
7. Визначити діаметр вала d (суцільного перерізу) з умови міцності.
8. Порівняти площі перерізів трубчастого і суцільного валів.
Дані взяти з табл. 3.2 і рис. 3.3.
Л і т е р а т у р а: [ І ] § 3.16; [ 2 ] § 6.4; [ 3 ] § 47-50; [ 4 ] § 4.6.
Таблиця 3.2 (дані до задачі 3)
| Букви алфа-віту | Схе- ма | Довжина, м | Моменти, кН∙м | 
МПа
| |||||
| а | в | с | Те1 | Те2 | Те3 | Те4 | |||
| А | 1,1 | 1,1 | 2,0 | 1,1 | 0,6 | 2,0 | 1,5 | ||
| Б | 1,2 | 1,2 | 1,9 | 1,2 | 0,7 | 1,9 | 1,4 | ||
| В | 1,3 | 1,3 | 1,8 | 1,3 | 0,8 | 1,8 | 1,3 | ||
| Г | 1,4 | 1,4 | 1,7 | 1,4 | 0,9 | 1,7 | 1,2 | ||
| Д | 1,5 | 1,5 | 1,6 | 1,5 | 1,0 | 1,6 | 1,1 | ||
| Е | 1,6 | 1,6 | 1,5 | 1,6 | 1,1 | 1,5 | 1,0 | ||
| Є | 1,7 | 1,7 | 1,4 | 1,7 | 1,2 | 1,4 | 0,9 | ||
| Ж | 1,8 | 1,8 | 1,3 | 1,8 | 1,3 | 1,3 | 0,8 | ||
| З | 1,9 | 1,9 | 1,2 | 1,9 | 1,4 | 1,2 | 0,7 | ||
| И | 2,0 | 2,0 | 1,1 | 2,0 | 1,5 | 1,1 | 0,6 | ||
| І | 1,1 | 1,9 | 2,0 | 1,1 | 0,6 | 2,0 | 0,5 | ||
| Ї | 1,2 | 1,8 | 1,9 | 1,2 | 0,7 | 1,9 | 1,5 | ||
| Й | 1,3 | 1,7 | 1,8 | 1,3 | 0,8 | 1,8 | 1,4 | ||
| К | 1,4 | 1,6 | 1,7 | 1,4 | 0,9 | 1,7 | 1,3 | ||
| Л | 1,5 | 1,8 | 1,6 | 1,5 | 1,0 | 1,6 | 1,2 | ||
| М | 1,6 | 1,4 | 1,5 | 1,6 | 1,1 | 1,5 | 1,1 | ||
| Н | 1,7 | 1,3 | 1,4 | 1,7 | 1,2 | 1,4 | 1,0 | ||
| О | 1,8 | 1,2 | 1,3 | 1,8 | 1,3 | 1,3 | 0,9 | ||
| П | 1,9 | 1,1 | 1,2 | 1,9 | 1,4 | 1,2 | 0,8 | ||
| Р | 2,0 | 1,5 | 1,1 | 2,0 | 1,5 | 1,1 | 0,7 | ||
| С | 1,1 | 1,6 | 2,0 | 1,1 | 0,6 | 2,0 | 0,6 | ||
| Т | 1,2 | 1,7 | 1,9 | 1,2 | 0,7 | 1,9 | 1,5 | ||
| У | 1,3 | 1,8 | 1,8 | 1,3 | 0,8 | 1,8 | 1,4 | ||
| Ф | 1,4 | 1,9 | 1,7 | 1,4 | 0,9 | 1,7 | 1,3 |
Продовження таблиці 3.2 (дані до задачі 3)
| Х | 1,5 | 2,0 | 1,6 | 1,5 | 1,0 | 1,6 | 1,2 | ||
| Ц | 1,6 | 1,9 | 1,8 | 1,6 | 1,1 | 1,5 | 1,1 | ||
| Ч | 1,7 | 1,8 | 1,4 | 1,7 | 1,2 | 1,4 | 1,0 | ||
| Ш | 1,8 | 1,7 | 1,3 | 1,8 | 1,3 | 1,3 | 0,9 | ||
| Щ | 1,9 | 1,6 | 1,2 | 1,9 | 1,4 | 1,2 | 0,8 | ||
| Ю | 2,0 | 1,5 | 1,1 | 2,0 | 1,5 | 1,1 | 0,7 | ||
| Я | 1,1 | 1,4 | 2,0 | 1,9 | 1,6 | 2,0 | 0,6 | ||
| Ь | 1,2 | 1,3 | 1,9 | 1,8 | 1,7 | 1,9 | 0,5 |
З а д а ч а № 4
Для заданого складеного перерізу (рис.3.4, табл.3.3) визначити положення головних центральних осей і величини головних центральних моментів інерції. Побудувати еліпс інерції.
Порядок розв’язування задачі
1. Виписати потрібні дані із таблиць сортаменту.
2. Накреслити переріз в масштабі на листі формату А4, де показати всі розміри.
3. Вибрати допоміжні координатні осі і визначити положення центра ваги складеного перерізу.
4. Провести центральні осі складеного перерізу (паралельні осям прокатних профілів). Обчислити значення осьових і відцентрового моментів інерції перерізу відносно центральних осей.
5. Визначити положення головних центральних осей і обчислити значення головних центральних моментів інерції.
6. Визначити головні радіуси інерції і побудувати еліпс інерції.
Л і т е р а т у р а: [ І ] § 2-10; [ 2 ] глава 4; [ 3 ] § 69-70; [ 4 ] глава 5.
Таблиця 3.3 (дані до задачі 4; 5)
| Букви алфа-віту | Схема | Швелер | Двотавр | Кутник рівно-бічний | Кутник нерів-нобічний | а/b |
| А | 12,5/8 | 0,25 | ||||
| Б | 14/9 | 0,1 | ||||
| В | 16/10 | 0,2 | ||||
| Г | 18/11 | 0,3 | ||||
| Д | 12,5 | 20/12,5 | 0,4 | |||
| Е | 14/9 | 0,5 | ||||
| Є | 25/16 | 0,6 | ||||
| Ж | 11/7 | 0,4 | ||||
| З | 12,5/8 | 0,3 | ||||
| И | 14/9 | 0,2 | ||||
| І, Ї | 16/10 | 0,1 | ||||
| Й | 18/11 | 0,2 | ||||
| К | 12,5 | 20/12,5 | 0,25 | |||
| Л | 25/16 | 0,3 | ||||
| М | 11/7 | 0,4 | ||||
| Н | 12,5/8 | 0,5 | ||||
| О | 14/9 | 0,6 | ||||
| П | 16/10 | 0,5 | ||||
| Р | 18/11 | 0,4 | ||||
| С | 20/12,5 | 0,3 | ||||
| Т | 12,5 | 25/16 | 0,25 | |||
| У | 11/7 | 0,2 | ||||
| Ф | 12,5/8 | 0,1 | ||||
| Х | 14/9 | 0,2 | ||||
| Ц | 16/10 | 0,25 | ||||
| Ч | 18/11 | 0,3 | ||||
| Ш | 20/12,5 | 0,4 | ||||
| Щ | 25/16 | 0,5 | ||||
| Ю | 12,5 | 11/7 | 0,4 | |||
| Я | 14/9 | 0,3 | ||||
| Ь | 18/11 | 0,2 |
Рис. 3.4. Схема складеного перерізу
З а д а ч а № 5
Для заданого складеного перерізу (рис. 3.5, табл. 3.3) визначити головні центральні моменти інерції.
Порядок розв’язування задачі
1. Виписати потрібні дані із таблиць сортаменту.
2. Накреслити переріз в масштабі.
3. Вибрати допоміжні координатні осі і визначити положення центра ваги складеного перерізу.
П р и м і т к а. За одну із допоміжних координатних осей вибрати вісь симетрії перерізу.
4. Через центр ваги складеного перерізу провести головні центральні осі і обчислити значення головних центральних моментів інерції.
Л і т е р а т у р а: [ І ] § 2-10; [ 2 ] глава 4; [3] § 69-70; [ 4 ] глава 5.
Рис. 3.5. Схема складеного перерізу
З а д а ч а № 6
Для заданих двох схем балок побудувати епюри поперечних сил і згинних моментів, визначити 
і підібрати розміри поперечного перерізу:
а) для схеми (а) діаметр круглого перерізу деревۥяної балки. При розрахунках прийняти 
;
б) для схеми (б) номер профіля двотавра. При розрахунках прийняти 
.
Дані взяти з табл. 3.4 і рис. 3.6.
Порядок розвۥязування задачі
1. Визначити опорні реакції.
2. Поділити кожну балку на ділянки і вказати границі ділянок.
3. Записати вирази М (х) і Q (х) для кожної ділянки і обчислити величини М (х) і Q (х) в характерних перерізах кожної ділянки.
4. Побудувати епюри поперечних сил і згинних моментів.
5. Підібрати поперечні перерізи балок.
Л і т е р а т у р а: [ І ] § 17-21, 60; [ 2 ] § 7.1-7.8; [ 3 ] § 58, 64; [ 4 ] § 4.7-7.7
Рис. 3.6. Розрахункова схема балки
Таблиця 3.4 (дані до задачі 6)
| Букви алфа-віту | а | b | c | d | e | f | F, кН | q, кН/м | M, кН∙м |
| м | |||||||||
| А | |||||||||
| Б | |||||||||
| В | |||||||||
| Г | |||||||||
| Д | |||||||||
| Е | |||||||||
| Є | |||||||||
| Ж | |||||||||
| З | |||||||||
| И | |||||||||
| І, Ї | |||||||||
| Й | |||||||||
| К | |||||||||
| Л | |||||||||
| М | |||||||||
| Н | |||||||||
| О | |||||||||
| П | |||||||||
| Р | |||||||||
| С | |||||||||
| Т | |||||||||
| У | |||||||||
| Ф | |||||||||
| Х | |||||||||
| Ц | |||||||||
| Ч | |||||||||
| Ш | |||||||||
| Щ | |||||||||
| Ю | |||||||||
| Я | |||||||||
| Ь |
З а д а ч а 7
Для заданої балки побудувати епюри поперечних сил і згинних моментів і підібрати двотавровий поперечний переріз. При розрахунках прийняти 
.
Побудувати епюру прогинів, вирахувавши дві ординати в прольоті балки і одну на консолі. Модуль пружності .
Дані взяти з табл. 3.5, рис. 3.7.
Рис.3.7. Розрахункова схема балки
Порядок розвۥязування задачі
1. Вибрати основну систему методу сил.
2. Побудувати епюру згинних моментів М від зовнішніх сил і вирахувати площі цих епюр.
3. Визначити опорні моменти, використовуючи „ рівняння трьох моментів ”.
4. Визначити опорні реакції.
5. Побудувати епюри згинних моментів М і поперечних сил Q.
6. Підібрати поперечний переріз балки.
7. Методом початкових параметрів визначити прогин в двох перерізах (в прольоті балки і на кінці консолі).
Л і т е р а т у р а: [ І ] § 63, 93; [ 2 ] § 9.8; [ 3 ] § 116, 117; [ 4 ] § 18.7.
Таблиця 3.5 (дані до задачі 7)
| Букви алфа-віту | Схема балки | F, кН | q, кН/м | l1, м | l2, м | а, м | M, кН∙м |
| А | 1,0 | ||||||
| Б | 2,0 | ||||||
| В | 3,0 | ||||||
| Г | 4,0 | ||||||
| Д | 1,2 | ||||||
| Е | 2,4 | ||||||
| Є | 3,6 | ||||||
| Ж | 4,8 | ||||||
| З | 1,0 | ||||||
| И | 2,0 | ||||||
| І, Ї | 3,0 | ||||||
| Й | 4,0 | ||||||
| К | 1,4 | ||||||
| Л | 2,2 | ||||||
| М | 3,4 | ||||||
| Н | 4,6 |
Продовження таблиці 3.5 (дані до задачі 7)
| О | 1,0 | ||||||
| П | 2,0 | ||||||
| Р | 3,0 | ||||||
| С | 4,0 | ||||||
| Т | 1,4 | ||||||
| У | 2,6 | ||||||
| Ф | 3,8 | ||||||
| Х | 4,2 | ||||||
| Ц | 1,0 | ||||||
| Ч | 2,0 | ||||||
| Ш | 3,0 | ||||||
| Щ | 4,0 | ||||||
| Ю | 1,0 | ||||||
| Я | 2,0 | ||||||
| Ь | 3,0 |
З а д а ч а 8
Дерев’яна балка (рис. 3.8) прямокутного поперечного перерізу навантажена вертикальною силою F в точці А і горизонтальною силою F в точці В (обидві точки розташовані на осі балки). На опорах балки виникають як вертикальні, так і горизонтальні реакції.
П о т р і б н о:
1. Побудувати епюри згинних моментів в вертикальній площині Мверт., горизонтальній площині Мгор. і визначити положення небезпечного перерізу;
2. Підібрати розміри поперечного перерізу h і b, якщо допустима напруга 
;
3. Визначити положення нейтральної лінії в небезпечному перерізі балки і побудувати для цього перерізу епюру нормальних напруг в аксонометрії.
Дані взяти з табл. 3.6, рис. 3.8.
Л і т е р а т у р а: [ І ] § 75; [ 2 ] § 8.1; [ 3 ] § 120; [ 4 ] § 19.
Рис.3.8. Розрахункова схема балки
Таблиця 3.6 (дані до задачі 8)
| Бук-ви ал-фа-віту | Схема | F, кН | l | a | 
| Бук-ви ал-фа-віту | Схема | F, кН | l | a |
|
| м | м | ||||||||||
| А | 1,0 | 1,1 | 0,2 | 1,6 | Н | 7,0 | 1,3 | 0,4 | 1,2 | ||
| Б | 2,0 | 1,2 | 0,3 | 1,7 | О | 8,0 | 1,2 | 0,3 | 1,3 | ||
| В | 3,0 | 1,3 | 0,4 | 1,8 | П | 9,0 | 1,1 | 0,2 | 1,4 | ||
| Г | 4,0 | 1,4 | 0,5 | 1,9 | Р | 10,0 | 1,0 | 0,3 | 1,5 | ||
| Д | 5,0 | 1,5 | 0,4 | 2,0 | С | 9,0 | 1,1 | 0,4 | 1,6 | ||
| Е | 6,0 | 1,6 | 0,3 | 1,1 | Т | 8,0 | 1,2 | 0,5 | 1,7 | ||
| Є | 7,0 | 1,7 | 0,2 | 1,2 | У | 7,0 | 1,3 | 0,4 | 1,8 | ||
| Ж | 8,0 | 1,8 | 0,3 | 1,3 | Ф | 6,0 | 1,4 | 0,3 | 1,9 | ||
| З | 9,0 | 1,9 | 0,4 | 1,4 | Х | 5,0 | 1,5 | 0,2 | 2,0 | ||
| И | 10,0 | 2,0 | 0,5 | 1,5 | Ц | 4,0 | 1,6 | 0,3 | 1,1 | ||
| І | 1,0 | 1,9 | 0,4 | 1,6 | Ч | 3,0 | 1,7 | 0,4 | 1,2 | ||
| Ї | 2,0 | 1,8 | 0,3 | 1,7 | Ш | 2,0 | 1,8 | 0,5 | 1,3 | ||
| Й | 3,0 | 1,7 | 0,2 | 1,8 | Щ | 1,0 | 1,9 | 0,4 | 1,4 | ||
| К | 4,0 | 1,6 | 0,3 | 1,9 | Ю | 2,0 | 2,0 | 0,3 | 1,5 | ||
| Л | 5,0 | 1,5 | 0,4 | 2,0 | Я | 3,0 | 1,9 | 0,2 | 1,6 | ||
| М | 6,0 | 1,4 | 0,5 | 1,1 | Ь | 4,0 | 1,8 | 0,3 | 1,7 |
З а д а ч а № 9
Короткий брус заданого поперечного перерізу (рис.3.9) стиснутий силою F, яка діє паралельно осі бруса і прикладена в точці К. Потрібно:
1. Побудувати епюру нормальних напруг в поперечному перерізі.
2. Визначити допустиме навантаження 
, якщо задані допустимі напруги на розтяг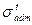 
і стиск 
.
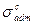3. Побудувати ядро поперечного перерізу.
Дані взяти з табл. 3.7, рис.3.9.
Порядок розв’язування задачі
1. Визначити положення центра ваги і головних центральних осей інерції перерізу, а також координати полюса (точки прикладання сили) відносно головних центральних осей.
2. Визначити площу перерізу, головні моменти інерції, квадрати головних радіусів інерції перерізу.
3. Вирахувати відрізки, які відтинає нейтральна лінія на осях координат, і показати положення нейтральної лінії.
4. Визначити координати небезпечних точок в розтягнутій і стиснутій зонах перерізу.
5. З умов міцності на розтяг і стиск вирахувати значення допустимих навантажень. Менше з них прийняти за .
6. Записати формулу для напруги в довільній точці. Вирахувати найбільшу розтягуючу і стискаючу напруги в поперечному перерізі та побудувати епюру напруг.
7. Визначити координати граничних (контурних) точок ядра перерізу. Побудувати ядро перерізу, вказавши на кресленні положення головних центральних осей, нейтральної лінії і полюса.
Л і т е р а т у р а: [ І ] § 76; [ 2 ] § 8.2; [ 3 ] § 123–124; [ 4 ] § 2.94;
3.9.
Таблиця 3.7 (дані до задачі 9)
| Букви алфавіту | Схема | a | b | 
| 
|
| м | МПа | ||||
| А | 0,20 | 0,20 | |||
| Б | 0,25 | 0,25 | |||
| В | 0,30 | 0,30 | |||
| Г | 0,35 | 0,35 | |||
| Д | 0,40 | 0,40 | |||
| Е | 0,45 | 0,35 | |||
| Є | 0,50 | 0,30 | |||
| Ж | 0,55 | 0,35 | |||
| З | 0,60 | 0,40 | |||
| И | 0,65 | 0,35 | |||
| І,Ї | 0,70 | 0,30 | |||
| К | 0,75 | 0,25 | |||
| Л | 0,80 | 0,20 | |||
| М | 0,85 | 0,25 | |||
| Н | 0,90 | 0,30 | |||
| О | 0,95 | 0,35 | |||
| П | 1,00 | 0,40 | |||
| Р | 0,95 | 0,35 | |||
| С | 0,90 | 0,30 | |||
| Т | 0,85 | 0,25 | |||
| У | 0,80 | 0,20 | |||
| Ф | 0,75 | 0,25 | |||
| Х | 0,70 | 0,30 | |||
| Ц | 0,65 | 0,35 | |||
| Ч | 0,60 | 0,40 | |||
| Ш | 0,55 | 0,35 | |||
| Щ | 0,50 | 0,30 | |||
| Ю | 0,45 | 0,25 | |||
| Я | 0,40 | 0,20 | |||
| Ь | 0,35 | 0,25 |
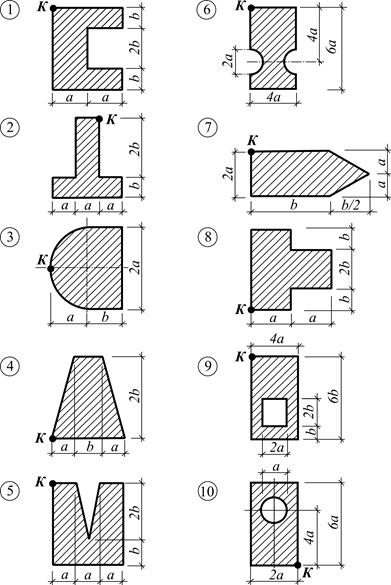
Рис. 3.9. Поперечний переріз бруса
З а д а ч а № 10
Бетонна гребля висотою Н навантажена тиском води та власною вагою (рис. 3.10). Визначити максимальну та мінімальну напруги і побудувати епюри нормальних напруг в небезпечному перерізі 
. Довжину греблі прийняти рівною 1 м. Необхідні для розв’язку задачі дані взяти з таблиці 3.8.
Рис. 3.10. Вертикальний переріз греблі
Послідовність розв’язку задачі
1. Вертикальний переріз греблі поділити на прості фігури та визначити їх площу.
2. Знайти рівнодійну тиску води на греблю та власну вагу окремих її частин. Показати напрямок всіх діючих навантажень на вертикальному розрізі греблі.
3. На основі принципу незалежності дії сил визначити найбільшу та найменшу нормальні напруги в поперечному перерізі як алгебраїчну суму напруг від дії кожного окремого навантаження.
4. Побудувати епюру розподілу напруг в перерізі .
Таблиця 3.8 (дані до задачі 10)
| Букви алфа-віту | Схема вертикального перерізу греблі | Н | h | b | a | Середня питома
вага бетону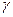 
(кН/м3)
|
| м | ||||||
| А | 7,0 | 4,0 | 4,0 | 1,0 | 18,0 | |
| Б | 6,9 | 4,1 | 4,1 | 1,1 | 18,5 | |
| В | 6,8 | 4,2 | 4,2 | 1,2 | 19,0 | |
| Г | 6,7 | 4,3 | 4,3 | 1,3 | 19,5 | |
| Д | 6,6 | 4,4 | 4,4 | 1,4 | 20,0 | |
| Е | 6,5 | 4,5 | 4,5 | 1,5 | 20,5 | |
| Є | 6,4 | 4,6 | 4,6 | 1,6 | 21,0 | |
| Ж | 6,3 | 4,7 | 4,7 | 1,7 | 21,5 | |
| З | 6,2 | 4,8 | 4,8 | 1,8 | 22,0 | |
| И | 6,1 | 4,9 | 4,9 | 1,9 | 22,5 | |
| І, Ї | 6,0 | 5,0 | 5,0 | 2,0 | 22,0 | |
| Й | 6,1 | 4,9 | 5,1 | 2,1 | 21,5 | |
| К | 6,2 | 4,8 | 5,2 | 2,2 | 21,0 | |
| Л | 6,3 | 4,7 | 5,3 | 2,3 | 20,5 | |
| М | 6,4 | 4,6 | 5,4 | 2,4 | 20,0 | |
| Н | 6,5 | 4,5 | 5,5 | 2,5 | 19,5 | |
| О | 6,6 | 4,4 | 5,4 | 2,4 | 19,0 | |
| П | 6,7 | 4,3 | 5,3 | 2,3 | 18,5 | |
| Р | 6,8 | 4,2 | 5,2 | 2,2 | 18,0 | |
| С | 6,9 | 4,1 | 5,1 | 2,1 | 18,5 | |
| Т | 7,0 | 4,0 | 5,0 | 2,0 | 19,0 | |
| У | 6,9 | 4,1 | 4,9 | 1,9 | 19,5 | |
| Ф | 6,8 | 4,2 | 4,8 | 1,8 | 20,0 | |
| Х | 6,7 | 4,3 | 4,7 | 1,7 | 20,5 | |
| Ц | 6,6 | 4,4 | 4,6 | 1,6 | 21,0 | |
| Ч | 6,5 | 4,5 | 4,5 | 1,5 | 21,5 | |
| Ш | 6,4 | 4,6 | 4,4 | 1,4 | 21,0 | |
| Щ | 6,3 | 4,7 | 4,3 | 1,3 | 22,5 | |
| Ю | 6,2 | 4,8 | 4,2 | 1,2 | 22,0 | |
| Я | 6,1 | 4,9 | 4,1 | 1,1 | 21,5 | |
| Ь | 6,0 | 5,0 | 4,0 | 1,0 | 21,0 |
З а д а ч а № 11
На вал круглого поперечного перерізу насаджені три шківи: ведучий, діаметром 
і два ведені, діаметром 
. Частота обертання ведучого шківа n обертів на хвилину. При цьому він передає потужність Р (кВт). Кожний ведений шків передасть потужність 
.
Паси ведучого шківа розташовані у вертикальній площині, ведених у горизонтальній і направлені в один бік.
Визначити діаметр вала 
, виходячи з третьої або четвертої теорій міцності, якщо допустима напруга 
= 80 МПа.
Дані взяти з табл. 3.9 і рис. 3.11.
Послідовність розв’язку задачі
1. Визначити діючі на вал скручувальні моменти.
2. Побудувати епюру крутних моментів Т.
3. Визначити сили 
і 
, що діють на шківи, і сили, які згинають вал.
4. Побудувати епюру згинних моментів від сил, що діють у вертикальній площині (власну вагу не враховувати).
5. Побудувати епюру згинних моментів від сил, що діють в горизонтальній площині.
6. Побудувати сумарну епюру згинних моментів 
.
7. Аналізуючи епюри Т (п.2) і (п.6), знайти небезпечний переріз і визначити діаметр вала.
Одержану з розрахунку величину заокруглити до найближчої більшої, що відповідно дорівнює: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 120, 140, 160, 180, 200 мм.
Л і т е р а т у р а: [ І ] § 77; [ 2 ] § 8.4; [ 3 ] § 125, 126; [ 4 ] § 4.9.
Рис. 3.11. Розрахункова схема вала
Таблиця 3.9 (дані до задачі 11)
| Букви алфа-віту | Схе-ма | Р, кВт | N, об/хв | а, м | b, м | c, м | ,
м
| ,
м
|
| А | 0,6 | 1,1 | 1,1 | 1,3 | 1,3 | |||
| Б | 0,7 | 1,2 | 1,2 | 1,4 | 1,4 | |||
| В | 0,8 | 1,3 | 1,3 | 1,5 | 1,5 | |||
| Г | 0,9 | 1,4 | 1,4 | 0,6 | 0,6 | |||
| Д | 1,0 | 1,5 | 1,5 | 0,7 | 0,7 | |||
| Е | 1,1 | 1,6 | 1,6 | 0,8 | 0,8 | |||
| Є | 1,2 | 1,7 | 1,7 | 0,9 | 0,9 | |||
| Ж | 1,3 | 1,8 | 1,8 | 1,0 | 1,0 | |||
| З | 1,4 | 1,5 | 1,0 | 1,1 | 1,1 | |||
| И | 0,6 | 1,0 | 1,1 | 1,2 | 1,2 | |||
| І, Ї | 0,7 | 1,1 | 1,2 | 1,3 | 1,3 | |||
| Й | 0,8 | 1,2 | 1,3 | 1,4 | 1,4 | |||
| К | 0,9 | 1,3 | 1,4 | 1,5 | 1,5 | |||
| Л | 1,0 | 1,4 | 1,5 | 1,6 | 1,6 | |||
| М |
