V2: Теория
V3: Общая
I: 117 Тема 4-7-7
S: Всякий факт, который может произойти в результате некоторого опыта (испытания) называют ###
+: событием
I: 118 Тема 4-7-7
S: Событие, которое в результате опыта может появиться, но может и не появиться называется ###
+: случайным
I: 119 Тема 4-7-7
S: Событие, которое неизбежно произойдет в данном опыте, называется ###
+: достоверным
I: 120 Тема 4-7-7
S: Событие, которое заведомо не происходит в данном опыте (испытании), называется ###
+: невозможным
I: 121 Тема 4-7-7
S: События, имеющие одинаковые условия и шансы появления называются ###
+: равновозможными
I: 122 Тема 4-7-7
S: Два события называются ###, если появление одного из них не исключает появление другого
+: совместными
I: 123 Тема 4-7-7
S: Вероятность ### события равна нулю
+: невозможного
I: 124 Тема 4-7-7
S: Вероятность ### события равна единице
+: достоверного
I: 125 Тема 4-7-7
S: Два несовместных события, образующие полную группу, называются ###
+: противоположными
I: 126 Тема 4-7-7
S: Вероятность каждого события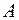 
есть величина, удовлетворяющая условию:
+: 
-: 
-: 
-: 
I: 127 ТЗ № 269
S: Классическое определение вероятности события А есть
+: 
-: 
-: 
-: 
I: 128 ТЗ № 270
S: Для вероятности невозможного события 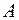верно:
+: 
-: 
-:
-: 
I: 129 ТЗ № 271
S: Для вероятности достоверного события 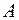верно
+:
-:
-:
-:
I: 130 ТЗ № 274
S: Вероятность суммы двух несовместных событий А и В равна:
+: 
-: 
-: 
-: 
I: 131 ТЗ № 274
S: Вероятность суммы двух совместных событий А и В равна:
-:
+:
-:
-:
I: 132 ТЗ № 275
S: Вероятность произведения двух событий равна
+: 
-: 
-: 
-: 
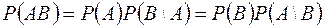
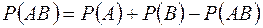
V2: Практика (к 4.1, 4.2)
I: 133 ТЗ № 324
S: Вероятность выбора из урны с 3 красными и 6 синими шарами одного красного равна
+: 
-: 
-: 
-: 
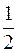
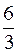
I: 134 ТЗ № 324
S: Вероятность выбора из урны с 5 красными и 10 синими шарами одного красного равна
+:
-:
-: 
-: 
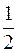
I: 135 ТЗ № 325
S: Вероятность выбора из урны с 5 белыми и 10 красными шарами одного белого равна
+: 
-: 
-: 
-: 
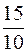
I: 136 ТЗ № 332
S: Вероятность выпадения четного числа при бросании игральной кости равна
+:
+:
-: 
-:
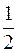
I: 137 ТЗ № 333
S: Вероятность выпадения нечетного числа при бросании игральной кости равна:
+:
+: 
-:
-:
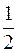
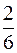
I: 138 ТЗ № 334
S: Вероятность выпадения "7" при бросании игральной кости равна:
+: 
-: 
-: 
-: 
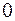
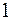
I: 139 ТЗ № 334
S: Вероятность выпадения "9" при бросании игральной кости равна:
+:
-:
-: 
-: 
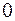
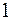
I: 140 ТЗ № 336
S: Вероятность успешной сдачи экзамена студентом, подготовившим 24 из 30 билетов, равна
+: 
+: 
-:
-: 
I: 141 ТЗ № 336
S: Вероятность успешной сдачи экзамена студентом, подготовившим 25 из 30 билетов, равна
+: 
+: 
-: 
-: 
I: 142 ТЗ № 337
S: Вероятность выбора из колоды в 36 карт карты бубновой масти равна
+: 
-: 
-: 
-: 
I: 143 ТЗ № 337
S: Вероятность выбора из колоды в 36 карт карты пиковой масти равна
+:
-:
-:
-:
I: 144 ТЗ № 334
S: Вероятность выбора из колоды в 36 карт карты червовой масти равна
+:
-:
-:
-:
I: 145 ТЗ № 337
S: Вероятность выбора из колоды в 36 карт карты дамы равна
+:
-: 
-: 
-:
I: 146 ТЗ № 341
S: Вероятность поражения цели тремя стрелками, при условии вероятности попадания каждого 0,7; 0,8; 0,7, равна
+: 
-: 
-: 
-: 
I: 147 ТЗ № 341
S: Вероятность поражения цели тремя стрелками, при условии вероятности попадания каждого 0,7; 0,8; 0,7, равна
+: 
-: 
-: 
-: 
I: 148 ТЗ № 346
S: Вероятность выбора карты с гласной буквой из 6 карт, образующих слово "хирург", равна
+:
+:
-: 
-:
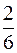
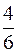
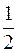
I: 149 ТЗ № 346
S: Вероятность выбора карты с гласной буквой из 8 карт, образующих слово "терапевт", равна
+: 
+: 
-: 
-:
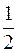
I: 150 ТЗ № 344
S: Вероятность того, что при выкладывании трех карт в ряд с буквами: О, К, Т образуется слово "КОТ", равна
+:
-:
-:
-: 
