V1: Теория множеств
V2: Теория
V3: Общая
I: 1 Тема 1-1-1
S: Любая четко определенная совокупность объектов называется ###
+: множеством
I: 2 Тема 1-1-1
S: Множество, которое не содержит никаких элементов, называется ###
+: пустым
: 5 Тема 1-1-1
I: 3 ТЗ № 112
S: Пустое множество принято обозначать:
+: 
-: 
-: 
-: 
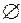
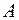
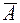
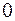
I: 4 ТЗ № 114
S: Множество В называется подмножеством множества ###, если каждый элемент множества В является элементом множества А
+: А
V3: Отношения между множествами
I: 5 Тема 1-1-2
S: Числовым называется множество, элементами которого являются:
+: числа
-: параметры
-: параметры и числа
-: множества
I: 6 ТЗ № 116
S: Если множество задано с помощью характеристического свойства, принята запись вида:
+: 
-: 
-: 
-: 
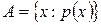
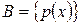
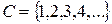
I: 7 ТЗ № 118
S: Если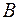 
- подмножество множества 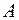, то принято писать
+: 
-: 
-: 
-: 
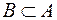
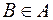
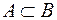
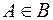
I: 8 ТЗ № 120
S: Множество 
есть множество всех ### чисел
+: натуральных
I: 9 ТЗ № 122
S: Множество 
есть множество всех ### чисел
+: целых
I: 10 ТЗ № 124
S: Если множество 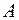включается в 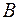, то принята запись:
-: 
-: 
+:
-: 
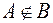
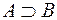
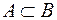
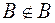
I: 11 ТЗ № 125
S: Верна запись:
+: 
-: 
-: 
-: 
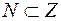
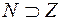
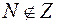
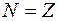
I: 12 ТЗ № 128
S: Верна запись:
+: 
-: 
-: 
-: 
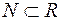
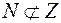
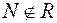
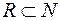
I: 13 ТЗ № 131
S: Если 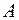- множество параллелограммов, 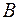- множество прямоугольников, то верна запись
+:
-:
-: 
-:
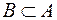
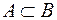
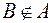
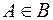
I: 14 ТЗ № 134
S: Если множество 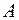не принадлежит 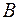, то принята запись:
+: 
-: 
-:
-:
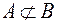
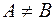
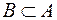
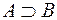
I: 15 ТЗ № 135
S: Есл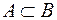и и 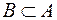, то множества 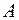и 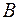называются ###
+: равными
I: 16 ТЗ № 136
S: Верна запись:
+: 
-: 
-: 
-: 
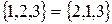
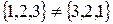
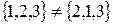
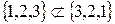
V3: Операции над множествами
I: 17 Тема 1-1-3
S: Множество, состоящее из элементов, принадлежащих А или В называется ### двух множеств А и В
+: объединением
I: 18 Тема 1-1-3
S: Множество, состоящее из элементов, которые принадлежат А иВ, называется ### двух множеств А и В
+: пересечением
I: 19 ТЗ № 140
S: Если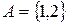 
, 
, то
+: 
-: 
-: 
-: 
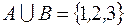
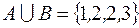
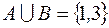
I:20 ТЗ № 141
S: Верна запись:
+: 
-: 
-: 
-: 
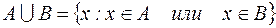
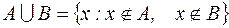
I: 21 ТЗ № 143
S: Если 
, то
+: 
-: 
-: 
: 
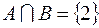
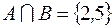
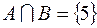
I: 22 ТЗ № 144
S: Верна запись:
-: 
+: 
-: 
-: 
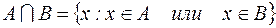
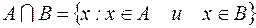
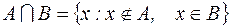
I: 23 ТЗ № 147
S: Если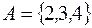 
, 
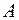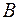, то разность между и есть
+: {2,4}
-: {5}
-: {3}
-: {2,3,4}
I: 24 ТЗ № 149
S: Запись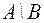 
означает
+: 
-: 
-: 
-: 
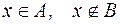
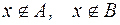
I: 25 ТЗ № 151
S: При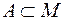 
разность 
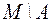принято обозначать
+:
-: 
-: 
-:
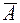
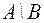
I:26 ТЗ № 153
S: Соответствие записей
L1: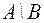
L2: 
L3: 
L4: 
L5:
R1: 
R2: 
R3: 
R4: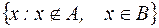 
R5: 
I: 27 ТЗ № 154
S: Для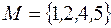 
, 
+: 
-: 
-: 
-: 
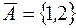
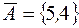
V2: Практика
I: 28 ТЗ № 171
S: Множество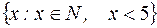 
задается перечислением:
+: 
-: 
-: 
-: 
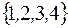
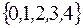
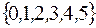
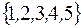
I: 29 ТЗ № 172
S: Множество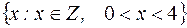 
задается перечислением:
+: 
-:
-: 
-:
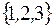
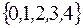
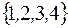
I: 30 ТЗ № 175
S: Множество 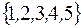задается с помощью характеристического свойства:
+: 
-: 
-: 
-: 
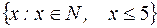
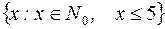
I: 31 ТЗ № 176
S: Множество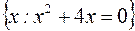 
задается перечислением
+: 
-: 
-: 
-: 
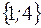
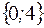
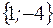
I: 32 ТЗ № 178
S: Отношением включения «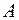 в 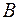» связаны
+: 
-: 
-: 
-: 
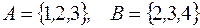
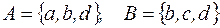
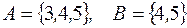
I: 33 ТЗ № 179
S: Множества 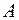и 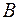равны между собой, если они имеют вид:
+: 
-: 
-: 
-: 
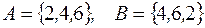
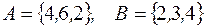
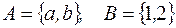
I: 34 ТЗ № 180
S: Объединением множеств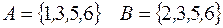 
является
+: 
-: 
-: 
-: 
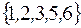
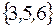
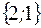
I: 35 ТЗ № 181
S: Для множеств 
множество 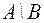имеет вид
+: 
-: 
-: 
-: 
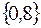
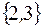
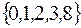
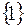
I: 36 ТЗ № 182
S: Для множеств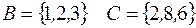 
множество 
имеет вид
+: 
-: 
-: 
-: 
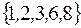
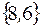
I: 37 ТЗ № 183
S: Для множеств 
множество имеет вид
+: 
-: 
-: 
-: 
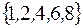
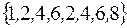
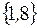
I: 38 ТЗ № 184
S: Для множеств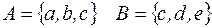 
множество имеет вид
+: 
-: 
-: 
-: 
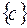
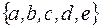
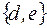
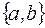
I: 39 ТЗ № 185
S: Для множеств 
множество 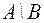имеет вид
+: 
-: 
-: 
-: 
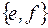
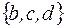
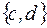
I: 40 ТЗ № 186
S: Для множеств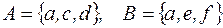 
множество 
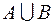имеет вид
+: 
-: 
-: 
-: 
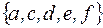
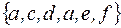
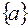
I: 41 ТЗ № 189
S: Равенство 
верно, если
+:
-: 
-: 
-: 
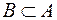
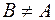
I: 42 ТЗ № 190
S: Равенство 
верно, если
+:
-:
-:
-: 
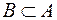
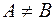
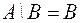
V1: Основы математического анализа
V2: Теория
I: 43 Тема 2-3-0
S: Последовательность, имеющая предел, называется ###
+: сходящейся
I: 44 Тема 2-3-0
S: Последовательность, не имеющая предела, называется ###
+: расходящейся
I: 45 Тема 2-3-0
S: Если последовательность сходится, то она имеет только один ###
+: предел
I: 46 Тема 2-3-0
S: Если последовательность ###, то она ограничена
+: сходится
I: 47 Тема 2-3-0
S: Переменная величина, предел которой неограниченно возрастает, называется бесконечно ### величиной
+: большой
I: 48 Тема 2-3-0
S: ### постоянной величины равен постоянной величине
+: Предел
I: 49 Тема 2-3-0
S: Предел ### нескольких функций равен сумме пределов этих функций
+: суммы
I: 50 Тема 2-3-0
S: Предел ### нескольких функций равен разности пределов этих функций
+: разности
I: 51 Тема 2-3-0
S: Предел ### нескольких функций равен произведению пределов этих функций
+: произведения
I: 52 Тема 2-3-0
S: Дифференциал постоянной величины равен ###
+: нулю
I: 53 Тема 2-3-0
S: Дифференциал ### равен разности дифференциалов
+: разности
I: 54 ТЗ № 199
S: Если для чисел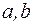 
при всех 
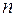имеет место неравенство 
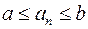, то последовательность называется ###
+: ограниченной
I: 55 ТЗ № 202
S: Если для последовательности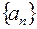 
существует число 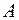, к которому числа 
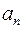приближаются как угодно близко, то это число называется ### последовательности
+: пределом
I: 56 ТЗ № 208
S: Функция 
имеет своим ### величину 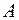, если ее переменная 
при своем приближении к 
устанавливает значение функции, близкое к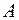
+: пределом
I: 57 ТЗ № 210
S: Первый замечательный предел имеет вид
+: 
-: 
-: 
-: 
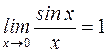
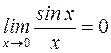
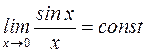
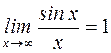
I: 58 ТЗ № 213
S: Второй замечательный предел имеет вид
+: 
-: 
-: 
-: 
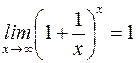
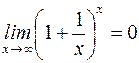
I: 59 ТЗ № 214
S: С помощью правила Лопиталя можно избежать неопределенности вида
+: 
-: 
-: 
-: 
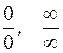
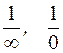
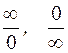
I: 60 ТЗ № 214
S: Дифференциал произведения вычисляется по формуле:
+: 
-: 
-: 
-: 
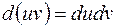
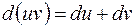
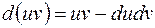
I: 61 ТЗ № 220
S: Дифференциал частного вычисляется по формуле:
+: 
-: 
-: 
-: 
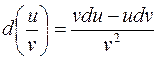
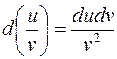
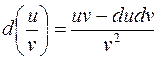
I: 62 ТЗ № 223
S: Формула интегрирования по частям имеет вид:
+: 
-: 
-: 
-: 
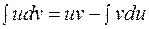
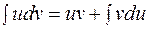
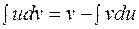
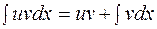
V2: Практика
I: 63 ТЗ № 227
S: Предел 
равен
+: 12
-: 90
-: 39
-: 9
I: 64 ТЗ № 228
S: Предел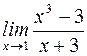 
равен
+: -1/2
-: 1/2
-: -2
-: 2/4
I: 65 ТЗ № 229
S: Предел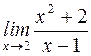 
равен
-: 4
+: 6
-: 4/5
-: 8
I: 66 ТЗ № 230
S: Предел 
равен
+: 
-: 
-: 
-:
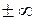
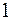
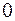
I: 67 ТЗ № 231
S: Предел 
равен
+:
-:
-: 
-: 
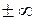
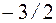
I: 68 ТЗ № 232
S: Производная функции 
равна
+: 
-: 
-: 
-: 
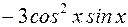
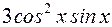
I: 69 ТЗ № 232
S: Производная функции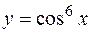 
равна
+: 
-: 
-: 
-: 
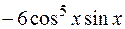
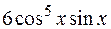
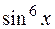
I: 70 ТЗ № 233
S: Производная функции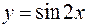 
равна
+: 
-: 
-: 
-: 
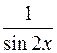
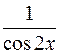
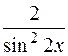
I: 71 ТЗ № 233
S: Производная функции 
равна
+: 
-:
-:
-:
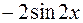
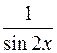
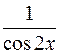
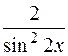
I: 72 ТЗ № 234
S: Производная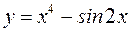 
равна
+: 
-: 
-: 
-: 
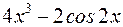
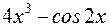
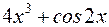
I: 73 ТЗ № 232
S: Производная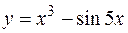 
равна
+: 
-: 
-: 
-: 
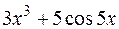
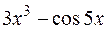
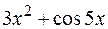
I:74 ТЗ № 235
S: Производная функции 
равна
+: 
-: 
-: 
-: 
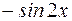
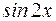
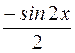
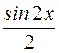
I:75 ТЗ № 235
S: Производная функции 
равна
+: 
-:
-:
-: 
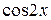
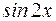
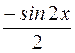
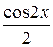
I: 76 ТЗ № 237
S: Интеграл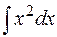 
равен
+: 
-: 
-: 
-: 
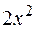
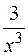
I: 77 ТЗ № 237
S: Интеграл 
равен
+: 
-: 
-: 
-:
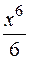
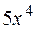
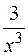
I: 78 ТЗ № 238
S: Интеграл 
равен
+: 
-: 
-: 
-: 
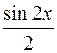
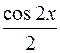
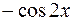
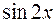
I: 79 ТЗ № 237
S: Интеграл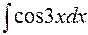 
равен
+: 
-: 
-: 
-: 
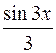
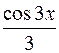
I: 80 ТЗ № 239
S: Интеграл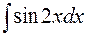 
равен
+: 
-: 
-: 
-: 
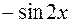
I: 81 ТЗ № 237
S: Интеграл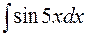 
равен
+: 
-: 
-: 
-: 
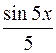
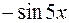
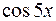
I: 82 ТЗ № 241
S: Производная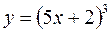 
равна
+: 
-: 
-: 
-: 
]
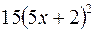
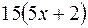
I: 83 ТЗ № 237
S: Производная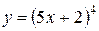 
равна
+: 
-: 
-: 
-: 
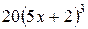
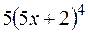
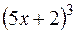
I: 84 ТЗ № 242
S: Производная функции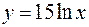 
равна
+: 
-: 
-: 
-: 
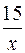
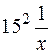
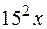
I: 85 ТЗ № 237
S: Производная функции 
равна
+: 
-: 
-: 
-: 
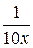
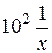
V1: Элементы комбинаторики
V2: Теория
I: 86 Тема 3-5-0
S: Соединения из n элементов по m, которые отличаются либо самими элементами, либо порядком элементов, называются ###
+: размещениями
I: 87 Тема 3-5-0
S: Соединения из n элементов, каждое из которых отличается лишь порядком элементов, называются ###
+: перестановками
I: 88 Тема 3-5-0
S: Размещение из n элементов по n принято называть ###
+: перестановкой
I: 89 Тема 3-5-0
S: Соединения из n элементов по m, которые отличаются хотя бы одним элементом, называются ###
+: сочетаниями
I: 90 ТЗ № 243
S: Формула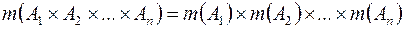 
выражает правило ###
+: умножения
I: 91 ТЗ № 244
S: Формула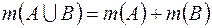 
выражает правило ###
+: сложения
I: 92 ТЗ № 246
S: Число размещений из 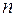элементов по 
определяется формулой
+: 
-: 
-: 
-: 
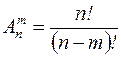
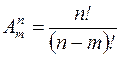
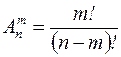
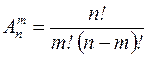
I: 93 ТЗ № 248
S: Для размещения с повторениями из 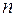элементов по принято:
+: 
-:
-: 
-: 
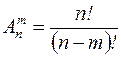
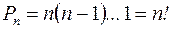
I: 94 ТЗ № 249
S: Верно равенство
+: 
-: 
-: 
-: 
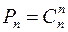
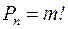
I: 95 ТЗ № 250
S: Число перестановок из 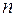элементов, каждое из которых содержит все 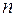элементов, вычисляется по формуле
+: 
-: 
-:
-: 
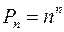
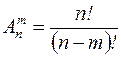
I: 96 ТЗ № 253
S: Для числа сочетаний из 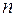элементов по принято обозначение
+: 
-: 
-: 
-: 
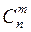
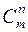
-: 97 ТЗ № 254
S: Верно равенство
+: 
-: 
-: 
-: 
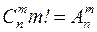
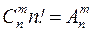
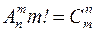
I: 98 ТЗ № 256
S: Формулой 
определяется число ### из 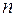по
+: сочетаний
V2: Практика
I: 99 Тема 3-6-0
S: Число способов выбора из 10 студентов группы старосты, профорга и спорторга равно
+: 720
-: 560
-: 120
-: 27
I: 100 Тема 3-6-0
S: Число способов выбора ручки или карандаша из 6 карандашей и 4 ручек равно
+: 10
-: 54
-: 2
-: 30
I: 101 Тема 3-6-0
S: Число способов выбора 2-х студентов из 10 равно
+: 45
-: 20
-: 12
-: 90
I: 102 Тема 3-6-0
S: Число способов выбора 2-х студентов на конференцию из 20 равно
+: 190
-: 380
-: 40
-: 22
I: 103 Тема 3-6-0
S: Из 4-х человек вариантов построения в строй существует
+: 24
-: 64
-: 256
-: 12
I: 104 Тема 3-6-0
S: Число способов перестановки букв в слове «ТЕСТЫ» равно
+: 60
-: 120
-: 30
-: 70
I: 105 Тема 3-6-0
S: Число способов перестановки букв в слове «КНИГА» равно
+: 120
-: 100
-: 60
-: 50
I: 106 Тема 3-6-0
S: Число способов выбора старосты курса из 3-х групп, в которых 10, 20, 15 студентов равно
+: 45
-: 3000
-: 1500
-: 200
I: 107 Тема 3-6-0
S: Число способов перестановки букв в слове «ИГРА» равно
+: 24
-: 48
-: 16
-: 256
I: 108 Тема 3-6-0
S: Число способов перестановки букв в слове «ШПРИЦ» равно
+: 120
-: 60
-: 720
-: 360
I: 109 Тема 3-6-0
S: В четырех пробирках имеются 4 различных препарата. Их можно поставить в штатив ### способами
+: 24
I: 110 Тема 3-6-0
S: Число способов проведения выборочного анализа у 2-х из 5 детей для проверки наличия инфекционного заболевания равно
+: 10
-: 20
-: 12
-: 24
I: 111 ТЗ № 260
S: Различных троек, выбирая первую букву из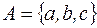 
, вторую – из 
, третью – из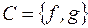 
можно образовать:
+: 12
-: 7
-: 10
-: 15
I: 112 З № 262
S: С помощью цифр множества 
можно записать различных трехзначных чисел:
+: 24
-: 20
-: 6
-: 4
I: 113 ТЗ № 263
S: Из цифр множества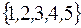 
можно составить трехзначных чисел всего
+: 60
-: 12
-: 120
-: 30
I: 114 ТЗ № 264
S: С помощью цифр множества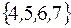 
можно составить трехзначных чисел всего
+: 64
-: 24
-: 9
-: 60
I: 115 ТЗ № 265
S: Из цифр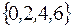 
можно составить различных трехзначных чисел всего
+: 18
-: 8
-: 24
-: 14
I: 116 ТЗ № 266
S: Из цифр 
можно составить трехзначных чисел всего
+: 36
-: 10
-: 48
-: 64
