Введение в анализ
1. Найти область определения функции 
Ответ: а)  ;
;
б)  (верный ответ);
(верный ответ);
в)  ;
;
г)  Æ.
Æ.
2. Найти область определения функции 
Ответ: а)  ;
;
б)  ;
;
в)  ;
;
г) 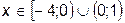 (верный ответ).
(верный ответ).
3. Найти область определения функции 
Ответ: а)  (верный ответ);
(верный ответ);
б)  ;
;
в)  ;
;
г)  .
.
4. Какие из указанных функций являются четными, какие нечетными, какие не являются ни четными, ни нечетными 1)  ; 2)
; 2)  ; 3)
; 3)  ?
?
Ответ: а) 1, 3 – четные, 2 – нечетная и не нечетная;
б) 1, 2 – не четные и не нечетные, 3 – четная;
в) все функции не являются ни четными и ни нечетными;
г) 1 – нечетная, 2 – не является ни четной, ни нечетной, 3 – четная (верный ответ).
5. Какие из перечисленных функций являются периодическими и какой у них наименьший положительный период 1)  ; 2)
; 2)  ; 3)
; 3)  ?
?
Ответ: а) 1 и 3 – периодические,  ;
;
б) 1 – периодическая,  , 2 – периодическая,
, 2 – периодическая,  ;
;
в) 1 – периодическая,  (верный ответ);
(верный ответ);
г) 1 – периодическая,  .
.
6. Зная график функции  , построить график функции
, построить график функции 
Ответ: а)  (верный ответ);
(верный ответ);
б) 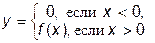 ;
;
в)  ;
;
г) 
7. Найти 
Ответ: а)  ;
;
б)  ;
;
в) 2(верный ответ);
г) 1.
8. Найти 
Ответ: а)  ;
;
б)  ;
;
в)  ;
;
г)  (верный ответ).
(верный ответ).
9. Найти 
Ответ: а) 0;
б)  ;
;
в) 1;
г)  (верный ответ).
(верный ответ).
10. Найти 
Ответ: а) 12(верный ответ);
б) 4;
в) 3;
г)  .
.
11. Найти 
Ответ: а)  ;
;
б) 3;
в) 2;
г) 1(верный ответ).
12. Найти 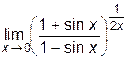
Ответ: а)  ;
;
б) 2;
в)  ;
;
г)  (верный ответ).
(верный ответ).
13. Найти 
Ответ: а) 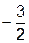 ;
;
б)  (верный ответ);
(верный ответ);
в)  ;
;
г)  .
.
14. Найти 
Ответ: а)  ;
;
б)  ;
;
в)  (верный ответ);
(верный ответ);
г) не существует.
15. Существует ли предел функции  в точках
в точках  и
и  ? Если существует, то чему равен?
? Если существует, то чему равен?
Ответ: а) в точке  существует и
существует и  , в точке
, в точке  не существует (верный ответ);
не существует (верный ответ);
б) в точках  и
и  пределы не существуют;
пределы не существуют;
в) пределы существуют:  ;
; 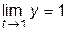 ;
;
г) в точке  предел не существует, а в точке
предел не существует, а в точке 
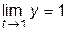 .
.
16. Найти точки разрыва функции  .
.
Ответ: а)  ;
;
б)  ;
;
в)  (верный ответ);
(верный ответ);
г)  .
.
17.  . Найти А и В, если известно, что функция не имеет точек разрыва.
. Найти А и В, если известно, что функция не имеет точек разрыва.
Ответ: а) А=0, В=1;
б) А=1, В=1;
в) А=2, В=2;
г) А=2, В=-2(верный ответ).
18.  . Найти b, если функция непрерывна для всех
. Найти b, если функция непрерывна для всех  .
.
Ответ: а) b=0;
б) b=1(верный ответ);
в) b=-1;
г) b=-2.
19. Найти точки разрыва функции и определить их характер  .
.
Ответ: а) точка разрыва  , устранимый разрыв(верный ответ);
, устранимый разрыв(верный ответ);
б) точка разрыва  , разрыв первого рода с конечным скачком;
, разрыв первого рода с конечным скачком;
в) односторонние пределы в точке  не существуют;
не существуют;
г) точек разрыва функция не имеет.
20. Функция  , где
, где  - неизвестная функция, непрерывна в точке,
- неизвестная функция, непрерывна в точке,  и ее
и ее  . Найти значения
. Найти значения  .
.
Ответ: а)  ;
;
б)  ;
;
в)  (верный ответ);
(верный ответ);
г)  .
.
21. Задана сходящаяся последовательность и  . Найти предел
. Найти предел  , если он существует.
, если он существует.
Ответ: а) ничего определенного сказать нельзя;
б)  ;
;
в)  (верный ответ);
(верный ответ);
г)  .
.
22. Функция 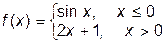 является
является
1) непрерывной на R;
2) непрерывной на R \{0} (верный ответ);
3) периодической на R;
4) ограниченной на R.
23. Функция  является
является
1) ограниченной на R;
2) периодической на R;
3) непрерывной на R (верный ответ);
4) монотонно убывающей на R.
24. Функция  является
является
1) монотонно убывающей на R;
2) ограниченной на R;
3) непрерывной на R (верный ответ);
4) периодической на R.
25. Функция  является
является
1) монотонно возрастающей на R;
2) непрерывной на R;
3) ограниченной на R;
4) непрерывной на R \{0} (верный ответ).
26. Функция  является
является
1) неограниченной на R;
2) периодической на R с периодом  (верный ответ);
(верный ответ);
3) монотонно возрастающей на R;
4) разрывной в точке  .
.
27. Функция  является
является
1) непрерывной при  (верный ответ);
(верный ответ);
2) периодической с периодом  ;
;
3) ограниченной при  ;
;
4) элементарной функцией при  .
.
28. Функция  является
является
1) ограниченной при  (верный ответ);
(верный ответ);
2) элементарной функцией при  ;
;
3) периодической функцией при  ;
;
4) монотонно возрастающей функцией при  .
.
29. Функция  является
является
1) элементарной на R;
2) непрерывной на R (верный ответ);
3) периодической на R;
4) монотонной на R.
30. Предел функции  равен
равен
1) 0 (верный ответ);
2) 2;
3)  ;
;
4) 3.
31. Предел функции  равен
равен
1) 1;
2)  (верный ответ);
(верный ответ);
3)  ;
;
4)  .
.
32. Предел функции  равен
равен
1)  (верный ответ);
(верный ответ);
2)  ;
;
3)  ;
;
4) 1.
33. Предел функции  равен
равен
1)  (верный ответ);
(верный ответ);
2)  ;
;
3)  ;
;
4)  .
.
34. Множество [1,3] является
1) неограниченным сверху;
2) неограниченным снизу;
3) ограниченным (верный ответ);
4) неограниченным и сверху и снизу.
35. Множество [1,+¥) является
1) неограниченным сверху (верный ответ);
2) ограниченным;
3) неограниченным снизу;
4) неограниченным сверху и снизу.
36. Точная верхняя грань множества  равна
равна
1) 1;
2) 2 (верный ответ);
3) 0;
4) 3.
37. Точная нижняя грань множества  равна
равна
1) 0;
2) 1 (верный ответ);
3) 2;
4)  .
.
38. Точная верхняя грань множества  равна
равна
1) 0;
2) 1 (верный ответ);
3) 2;
4) 3.
39. Точная нижняя грань множества  равна
равна
1)  (верный ответ);
(верный ответ);
2)  ;
;
3)  ;
;
4) 0.
Дифференциальное исчисление
1. Производная функции 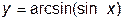 в точке
в точке  равна:
равна:
Ответ: 1) 1;
2) –1;
3) 0;
4) не определена (верный ответ).
2. Сумма значений производной функции  в точках
в точках  и
и  равна:
равна:
Ответ: 1)  ;
;
2)  (верный ответ);
(верный ответ);
3)  ;
;
4) другой ответ.
3. Значение производной функции  в точке
в точке  равно:
равно:
Ответ: 1) 1;
2) меньше единицы;
3) больше единицы;
4) не определено (верный ответ).
4. Производная функции 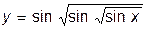 имеет вид:
имеет вид:
Ответ: 1)  ;
;
2)  (верный ответ);
(верный ответ);
3)  ;
;
4) другой ответ.
5. Производная функции  имеет вид:
имеет вид:
Ответ: 1)  (верный ответ);
(верный ответ);
2)  ;
;
3)  ;
;
4) другой ответ.
6. Значение производной функции  в точке
в точке  равно:
равно:
Ответ: 1) –1;
2) 0;
3) 1;
4) не определено (верный ответ).
7. Существование конечных односторонних производных функции  в точке
в точке  является:
является:
Ответ: 1) достаточным условием дифференцируемости функции в этой точке;
2) необходимым условием дифференцируемости функции в этой точке (верный ответ);
3) необходимым и достаточным условием дифференцируемости функции в этой точке;
4) ни одно из высказываний 1-3 не имеет места.
8. Точка движется прямолинейно по закону  . Тогда скорость ее в момент времени
. Тогда скорость ее в момент времени  равна:
равна:
Ответ: 1) 1 (верный ответ);
2) 2;
3) 3,5;
4) другой ответ.
9. Производная неявной функции 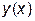 , заданной уравнением
, заданной уравнением  при
при  имеет значение:
имеет значение:
Ответ: 1) 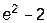 ;
;
2) 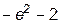 (верный ответ);
(верный ответ);
3) 1;
4)  .
.
10. Функция 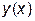 задана параметрически системой уравнений:
задана параметрически системой уравнений:  . Производная
. Производная  равна:
равна:
Ответ: 1)  ;
;
2)  (верный ответ);
(верный ответ);
3) 1;
4)  .
.
11. Производная четной дифференцируемой функции является:
Ответ: 1) четной функцией;
2) нечетной функцией (верный ответ);
3) ни четной, ни нечетной функцией;
4) невозможно определить.
12. Производная дифференцируемой периодической функции является:
Ответ: 1) периодической функцией с тем же периодом (верный ответ);
2) периодической функцией возможно с другим периодом;
3) непериодической функцией;
4) невозможно определить.
13. Площадь треугольника, образованного осями координат и касательной к графику функции 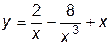 в точке с абсциссой
в точке с абсциссой  равна:
равна:
Ответ: 1) 2;
2) 1 (верный ответ);
3) 5;
4)  .
.
14. Парабола  пересекает ось абсцисс в начале координат под углом 45о при значении параметра а, равном:
пересекает ось абсцисс в начале координат под углом 45о при значении параметра а, равном:
Ответ: 1) 1;
2) 3;
3) 4 (верный ответ);
4) другой ответ.
15.  ;
;  равна:
равна:
Ответ: 1) 4×124!;
2) 0 (верный ответ);
3) 123!;
4) 4×14!
16. 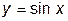 ;
;  равна:
равна:
Ответ: 1)  (верный ответ);
(верный ответ);
2)  ;
;
3) 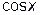 ;
;
4)  .
.
17. Координаты точки на графике функции  , в которой касательная, проведенная к графику, будет перпендикулярна прямой
, в которой касательная, проведенная к графику, будет перпендикулярна прямой  , равны:
, равны:
Ответ: 1) (1;2);
2)  ;
;
3) (-1;-4);
4) такой точки не существует (верный ответ).
18. Найти дифференциал функции 
Ответ: а)  (верный ответ);
(верный ответ);
б)  ;
;
в)  ;
;
г)  .
.
19. Найти дифференциал функции 
Ответ: а)  ;
;
б)  (верный ответ);
(верный ответ);
в)  ;
;
г)  .
.
20. Найти дифференциал функции 
Ответ: а)  ;
;
б)  ;
;
в)  (верный ответ);
(верный ответ);
г)  .
.
21. Найти дифференциал функции 
Ответ: а)  ;
;
б)  ;
;
в)  ;
;
г)  (верный ответ).
(верный ответ).
22. Найти дифференциал функции 
Ответ: а)  (верный ответ);
(верный ответ);
б)  ;
;
в)  ;
;
г)  .
.
23. Найти дифференциал второго порядка функции 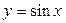
Ответ: а)  ;
;
б)  (верный ответ);
(верный ответ);
в)  ;
;
г)  .
.
24. Найти дифференциал второго порядка функции 
Ответ: а)  ;
;
б)  ;
;
в)  (верный ответ);
(верный ответ);
г)  .
.
25. Найти дифференциал второго порядка функции 
Ответ: а)  ;
;
б)  ;
;
в)  ;
;
г)  (верный ответ).
(верный ответ).
26. Найти дифференциал второго порядка функции 
Ответ: а)  (верный ответ);
(верный ответ);
б)  ;
;
в)  ;
;
г)  .
.
27. Найти дифференциал второго порядка функции 
Ответ: а)  ;
;
б)  (верный ответ);
(верный ответ);
в)  ;
;
г)  .
.
28. Написать уравнение касательной к кривой  в точке с абсциссой
в точке с абсциссой 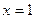
Ответ: а)  (верный ответ);
(верный ответ);
б)  ;
;
в)  ;
;
г)  .
.
29. Написать уравнение касательной к кривой  в точке с абсциссой
в точке с абсциссой 
Ответ: а)  ;
;
б) 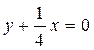 ;
;
в)  ;
;
г)  (верный ответ).
(верный ответ).
30. Написать уравнение касательной к кривой  в точке с абсциссой
в точке с абсциссой 
Ответ: а)  ;
;
б)  (верный ответ);
(верный ответ);
в)  ;
;
г) 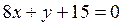 .
.
31. Написать уравнение касательной к кривой  в точке с абсциссой
в точке с абсциссой 
Ответ: а)  ;
;
б)  ;
;
в)  (верный ответ);
(верный ответ);
г)  .
.
32. Написать уравнение касательной к кривой  в точке с абсциссой
в точке с абсциссой 
Ответ: а)  (верный ответ);
(верный ответ);
б)  ;
;
в)  ;
;
г)  .
.
33. Написать уравнение нормали к кривой  в точке с абсциссой
в точке с абсциссой 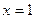
Ответ: а)  ;
;
б)  ;
;
в)  ;
;
г)  (верный ответ).
(верный ответ).
34. Написать уравнение нормали к кривой  в точке с абсциссой
в точке с абсциссой 
Ответ: а) 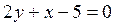 ;
;
б)  ;
;
в)  (верный ответ);
(верный ответ);
г)  .
.
35. Написать уравнение нормали к кривой  в точке с абсциссой
в точке с абсциссой 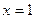
Ответ: а)  ;
;
б)  (верный ответ);
(верный ответ);
в)  ;
;
г)  .
.
36. Написать уравнение нормали к кривой  в точке с абсциссой
в точке с абсциссой 
Ответ: а)  (верный ответ);
(верный ответ);
б)  ;
;
в)  ;
;
г)  .
.
37. Написать уравнение нормали к кривой  в точке с абсциссой
в точке с абсциссой 
Ответ: а) 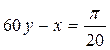 ;
;
б)  (верный ответ);
(верный ответ);
в)  ;
;
г)  .
.
38. Найти точку на кривой  , касательная в которой перпендикулярна прямой
, касательная в которой перпендикулярна прямой 
Ответ: а)  ;
;
б)  (верный ответ);
(верный ответ);
в)  ;
;
г) 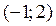 .
.
39. Найти точку на кривой  , касательная в которой параллельна прямой
, касательная в которой параллельна прямой 
Ответ: а)  ;
;
б)  (верный ответ);
(верный ответ);
в)  ;
;
г)  .
.
Приложения производной
1.  равен:
равен:
Ответ: 1) 1;
2)  (верный ответ);
(верный ответ);
3) 0;
4)  .
.
2.  равен:
равен:
Ответ: 1) 4;
2)  ;
;
3)  (верный ответ);
(верный ответ);
4)  .
.
3.  равен:
равен:
Ответ: 1) 2;
2) -2;
3) 0;
4)  (верный ответ).
(верный ответ).
4.  равен:
равен:
Ответ: 1)  ;
;
2) 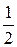 (верный ответ);
(верный ответ);
3)  ;
;
4)  .
.
5. Предел функции  равен
равен
1)  (верный ответ);
(верный ответ);
2)  ;
;
3)  ;
;
4)  .
.
6. Предел функции  равен
равен
1)  (верный ответ);
(верный ответ);
2) 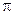 ;
;
3) 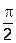 ;
;
4)  .
.
7. Предел функции  равен
равен
1)  (верный ответ);
(верный ответ);
2)  ;
;
3)  ;
;
4)  .
.
8. Предел функции  равен
равен
1) –4 (верный ответ);
2) –3;
3)  ;
;
4)  .
.
9.  равен:
равен:
Ответ: 1) -1;
2) 1(верный ответ);
3) не существует;
4) -2.
10.  равен:
равен:
Ответ: 1)  ;
;
2)  ;
;
3) не существует;
4)  (верный ответ).
(верный ответ).
11.  равен:
равен:
Ответ: 1)  ;
;
2)  (верный ответ);
(верный ответ);
3)  ;
;
4) 5.
12.  равен:
равен:
Ответ: 1)  (верный ответ);
(верный ответ);
2)  ;
;
3) 3;
4) 5.
13.  равен:
равен:
Ответ: 1) 1;
2)  (верный ответ);
(верный ответ);
3)  ;
;
4) 0.
14. Функция  является монотонной на промежутках:
является монотонной на промежутках:
Ответ: 1) 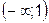 ;
;
2)  ;
;
3)  ;
;
4)  (верный ответ).
(верный ответ).
15. Если функция  убывает при всех значениях x, то значение параметра а принадлежит промежутку:
убывает при всех значениях x, то значение параметра а принадлежит промежутку:
Ответ: 1)  ;
;
2)  (верный ответ);
(верный ответ);
3) 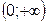 ;
;
4)  .
.
16. Промежутками возрастания функции 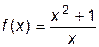 является:
является:
Ответ: 1)  (верный ответ);
(верный ответ);
2)  ;
;
3)  ;
;
4)  .
.
17. Значения параметра а, при которых функция  возрастает на всей числовой оси, принадлежит промежутку:
возрастает на всей числовой оси, принадлежит промежутку:
Ответ: 1) 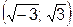 ;
;
2)  (верный ответ);
(верный ответ);
3) 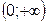 ;
;
4) 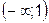 .
.
18. Число действительных корней производной многочлена  равно:
равно:
Ответ: 1) 3 (верный ответ);
2) 4;
3) 2;
4) невозможно определить.
19. Значения параметра а, при которых функция  не имеет критических точек, принадлежат промежутку:
не имеет критических точек, принадлежат промежутку:
Ответ: 1)  ;
;
2)  ;
;
3)  или
или  (верный ответ);
(верный ответ);
4) другой ответ.
20. Значения параметра а, при которых функция  не имеет критических точек, принадлежат промежутку:
не имеет критических точек, принадлежат промежутку:
Ответ: 1) 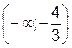 ;
;
2) 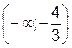 или
или  (верный ответ);
(верный ответ);
3)  ;
;
4) другой ответ.
21. Значения параметра а, при которых среди корней уравнения  имеются два равных, следующие:
имеются два равных, следующие:
Ответ: 1)  (верный ответ);
(верный ответ);
2)  ;
;
3)  ;
;
4)  .
.
22. Уравнение  имеет:
имеет:
Ответ: 1) только один действительный корень (верный ответ);
2) три действительных корня, среди которых два равных;
3) три различных действительных корня;
4) другой ответ.
23. Если трехчлен  имеет минимум при
имеет минимум при  , причем этот минимум равен 5, то значения параметров
, причем этот минимум равен 5, то значения параметров  и
и 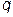 равны:
равны:
Ответ: 1)  ;
;
2)  (верный ответ);
(верный ответ);
3)  ;
;
4)  .
.
24. Все корни многочлена  действительные и разные. Тогда производная этого многочлена имеет:
действительные и разные. Тогда производная этого многочлена имеет:
Ответ: 1) n действительных корней;
2) по крайней мере (n -1) действительный корень;
3) точно (n -1) действительный корень (верный ответ);
4) невозможно определить.
25. Наибольшее значение параметра а, при котором 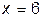 является точкой экстремума функции
является точкой экстремума функции  , равно:
, равно:
Ответ: 1) 10;
2) 5;
3) 7 (верный ответ);
4) –3.
26. Значение параметра с, при котором функция  не имеет экстремума в критической точке, равно:
не имеет экстремума в критической точке, равно:
Ответ: 1) 1,92 (верный ответ);
2) –10,08;
3) 2;
4) –10.
27. Число точек экстремума функции  равно:
равно:
Ответ: 1) 2;
2) 3;
3) 6;
4) 1 (верный ответ).
28. Наименьшее значение функции  на отрезке
на отрезке  равно:
равно:
Ответ: 1)  ;
;
2)  ;
;
3)  (верный ответ);
(верный ответ);
4) другой ответ.
29. Точка  является точкой перегиба кривой
является точкой перегиба кривой  при значениях параметров а и b, равных:
при значениях параметров а и b, равных:
Ответ: 1) 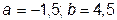 (верный ответ);
(верный ответ);
2)  ;
;
3)  ;
;
4) другой ответ.
30. Уравнение касательной к графику функции  в точке минимума этой функции имеет вид:
в точке минимума этой функции имеет вид:
Ответ: 1)  ;
;
2)  (верный ответ);
(верный ответ);
3)  ;
;
4)  .
.
31. График функции  является выпуклой кривой на интервале:
является выпуклой кривой на интервале:
Ответ: 1)  ;
;
2)  (верный ответ);
(верный ответ);
3)  ;
;
4) другой ответ.
32. Число асимптот графика функции  равно:
равно:
Ответ: 1) 2;
2) 1;
3) 3 (верный ответ);
4) 0.
33. Функция  принимает наименьшее значение на отрезке
принимает наименьшее значение на отрезке 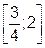 в точке:
в точке:
Ответ: 1)  ;
;
2) 1 (верный ответ);
3) 2;
4)  .
.
34. Представление числа 12 в виде суммы двух положительных слагаемых, таких что сумма их квадратов принимает наименьшее значение, имеет вид:
Ответ: 1) 4+8;
2) 6+6 (верный ответ);
3) 5+7;
4) 3+9.
35. График четной функции имеет асимптоту  при
при  . Тогда уравнение асимптоты при
. Тогда уравнение асимптоты при  имеет вид:
имеет вид:
Ответ:  (верный ответ);
(верный ответ);
2) 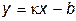 ;
;
3)  ;
;
4) невозможно определить.
36. Кривая  имеет следующие асимптоты:
имеет следующие асимптоты:
Ответ: 1)  ;
;
2)  (верный ответ);
(верный ответ);
3)  ;
;
4) только  .
.
37. Функция  принимает наименьшее значение на отрезке
принимает наименьшее значение на отрезке 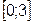 в точке:
в точке:
Ответ: 1) 0;
2) 1;
3) 2 (верный ответ);
4) 3.
38. Найти наибольшее и наименьшее значения функции  на отрезке
на отрезке 
Ответ: а)  ,
, 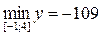 (верный ответ);
(верный ответ);
б)  ,
, 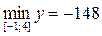 ;
;
в)  ,
,  ;
;
г)  ,
,  .
.
39. Найти наибольшее и наименьшее значения функции  на отрезке
на отрезке 
Ответ: а)  ,
, 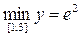 ;
;
б)  ,
, 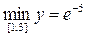 ;
;
в)  ,
,  (верный ответ);
(верный ответ);
г)  ,
,  .
.
40. Найти наибольшее и наименьшее значения функции  на отрезке
на отрезке 
Ответ: а)  ,
,  ;
;
б)  ,
,  (верный ответ);
(верный ответ);
в)  ,
, 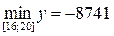 ;
;
г)  ,
,  .
.
41. Найти наибольшее и наименьшее значения функции  на отрезке
на отрезке 
Ответ: а)  ,
,  ;
;
б)  ,
, 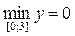 ;
;
в)  ,
, 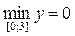 ;
;
г)  ,
, 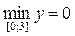 (верный ответ).
(верный ответ).
42. Найти наибольшее и наименьшее значения функции  на отрезке
на отрезке 
Ответ: а)  ,
,  ;
;
б) 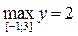 ,
,  ;
;
в)  ,
,  (верный ответ);
(верный ответ);
г)  ,
,  .
.






