Если действуют несколько сосредоточенных сил, то для одной силы Pi, согласно ответу на вопрос М.7.9, имеем

При нескольких сосредоточенных силах получим

Коэффициенты Ki определяются каждый раз отдельно для своих значений ri / z, так как радиус  для каждой силы свой.
для каждой силы свой.
М.7.12*. Как строится решение задачи для силы, приложенной на границе полуплоскости? Как соблюсти условие размерностей в этом случае?
В случае плоской задачи решение строится таким же образом, как и в пространственной задаче (см.вопрос М.7.9). В качестве аргументов используются: сосредоточенная сила P (в случае плоской задачи она имеет разномерность Н/м в отличие от пространственной, где размерность силы в H), угол между радиусом и вертикалью q и радиус r. Для того, чтобы левая и правая части имели одинаковые размерности, числитель следует разделить не на квадрат радиуса, как в пространственной задаче, а на радиус в первой степени. Следовательно, получим

М.7.13*. Как определяется безразмерный коэффициент A1 в формуле для s r (см.М.7.12) и в чем отличие в его определении по сравнению с пространственной задачей?
Безразмерный коэффициент A 1 определяется из условия равновесия путем проектирования напряжений s r, умноженных на величину элементарной площадки, на вертикальную ось. В данном случае берется не полусфера, как в пространственной задаче, а полукольцо. Коэффициент после интегрирования оказывается равным A 1=2/p, поэтому
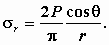
М.7.14. Как выглядят эпюры напряжений при действии сосредоточенной силы в случае плоской задачи и чем они отличаются от эпюр пространственной задачи?
Эпюры напряжений в случае плоской задачи имеют тот же вид, что и в пространственной задаче, однако ординаты их другие. Напряжения в случае плоской задачи рассеиваются как бы медленнее, чем в случае пространственной задачи.
М.7.15. Какое условие накладывается на эпюры напряжений для выполнения условия равновесия?
Для выполнения условия равновесия необходимо, чтобы в случае пространственной задачи объем эпюры s z при заданной постоянной величине z равнялся бы действующей сосредоточенной силе.
В случае плоской задачи это условие сохраняется, однако оно упрощается, и поэтому площадь эпюры s z при постоянной величине z должна быть равна внешней нагрузке.
М.7.16*. От каких характеристик деформируемости зависят напряжения в случае пространственной и плоской задач о сосредоточенной силе на поверхности?
В случае пространственной задачи ряд напряжений, в том числе s z, не зависят от характеристик деформируемости, а остальные зависят от коэффициента Пуассона m 0. В случае плоской задачи все напряжения отm 0 не зависят.






