1. Теоретичні відомості
Нехай 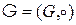
 – скінчена група. Розглянемо шифросистему
– скінчена група. Розглянемо шифросистему  . Інформація представляється послідовністю
. Інформація представляється послідовністю  . Сеансовий ключ – (потенційно нескінчена) періодична послідовність
. Сеансовий ключ – (потенційно нескінчена) періодична послідовність  – «гамма», тобто накладається на інформацію, що генерується, за допомогою порозрядної групової операції
– «гамма», тобто накладається на інформацію, що генерується, за допомогою порозрядної групової операції  . Таким чином, шифротекст має вид
. Таким чином, шифротекст має вид
 ,
,
де 
 . Такий шифр називають іноді шифром Віженера (або шифром Вернама).
. Такий шифр називають іноді шифром Віженера (або шифром Вернама).
Криптоаналіз шифросистеми  може бути здійснений у відповідності до такої схеми, що складається з двох етапів: на 1-у етапі обчислюється період
може бути здійснений у відповідності до такої схеми, що складається з двох етапів: на 1-у етапі обчислюється період 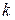 сеансового ключа
сеансового ключа  , а на 2-у етапі – сам сеансовий ключ
, а на 2-у етапі – сам сеансовий ключ  .
.
1-й етап (тобто обчислення періоду 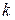 сеансового ключа) здійснюється у відповідності до методу Ф. Казіскі (1863р.):
сеансового ключа) здійснюється у відповідності до методу Ф. Казіскі (1863р.):
Два однакових відрізка відкритого тексту, що відстоять один від одного на відстані 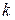 , зашифровані однаково.
, зашифровані однаково.
Індексом збігу в послідовності  називається ймовірність того, що збігаються два випадково обраних елементи цієї послідовності. Цей індекс обчислюється у відповідності до формули:
називається ймовірність того, що збігаються два випадково обраних елементи цієї послідовності. Цей індекс обчислюється у відповідності до формули:
 ,
,
де 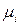
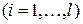 – число входжень елементу
– число входжень елементу  в послідовність
в послідовність  .
.
Нехай 
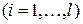 – ймовірність появи елементу
– ймовірність появи елементу  в осмисленому тексті. Тоді
в осмисленому тексті. Тоді

для будь-якого осмисленого тексту  .
.
За допомогою цієї формули можуть бути підраховані індекси збігу в осмисленому тексті для будь-якої природної мови. Для деяких європейських мов такі індекси наведені в таблиці 5.1.
Таблиця 5.1
| Мова | Російська | Англ. | Франц. | Нім. | Італ. | Іспан. |

| 0.0529 | 0.0662 | 0.0778 | 0.0762 | 0.0738 | 0.0775 |
Обчислення періоду 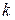 сеансового ключа
сеансового ключа  здійснюється в такий спосіб. Представимо шифротекст
здійснюється в такий спосіб. Представимо шифротекст  в виді матриці
в виді матриці
 .
.
Якщо  , то для кожного стовпця
, то для кожного стовпця 
 матриці
матриці 
 ,
,
оскільки кожний стовпець 
 матриці
матриці  – це результат застосування фіксованої циклічної перестановки
– це результат застосування фіксованої циклічної перестановки  , визначеної на множині
, визначеної на множині  .
.
Якщо ж  , то
, то
 ,
,
де  – індекс збігу у випадковому тексті природної мови, яка використовується.
– індекс збігу у випадковому тексті природної мови, яка використовується.
Оскільки для будь-якої природної мови  , то обчислення періоду
, то обчислення періоду 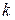 сеансового ключа
сеансового ключа  не складає особливих зусиль.
не складає особливих зусиль.
2-й етап (тобто обчислення сеансового ключа при відомому його періоді 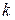 ) здійснюється в такий спосіб.
) здійснюється в такий спосіб.
Взаємним індексом збігу в послідовностях  і
і  називається ймовірність того, що випадково обраний елемент послідовності
називається ймовірність того, що випадково обраний елемент послідовності 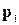 збігається з випадково обраним елементом послідовності
збігається з випадково обраним елементом послідовності  . Взаємний індекс збігу в послідовностях
. Взаємний індекс збігу в послідовностях 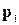 і
і  обчислюється у відповідності до формули:
обчислюється у відповідності до формули:
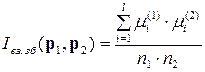 ,
,
де 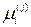
 – число входжень елементу
– число входжень елементу  в послідовність
в послідовність  . Оскільки період
. Оскільки період 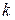 сеансового ключа
сеансового ключа  відомий, то відома матриця
відомий, то відома матриця
 ,
,
де кожний стовпець 
 отриманий в результаті застосування фіксованої циклічної перестановки
отриманий в результаті застосування фіксованої циклічної перестановки  , що визначена на множині
, що визначена на множині  .
.
Розглянемо аналіз матриці  , якщо
, якщо  , де
, де  для всіх
для всіх  . Кожна циклічна перестановка
. Кожна циклічна перестановка 
 має вид
має вид
 ,
,
тобто представляє собою відносний зсув на величину  . Звідси витікає, що
. Звідси витікає, що
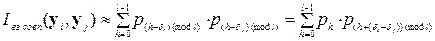 ,
,
де  – ймовірність появи елементу
– ймовірність появи елементу  в відкритому тексті. А оскільки
в відкритому тексті. А оскільки
 ,
,
то стовпці  і
і  з відносними зсувами на величини
з відносними зсувами на величини  і
і  мають однакові взаємні індекси збігу. По аналогії з індексами збігу, взаємні індекси збігу при зсуві на величину
мають однакові взаємні індекси збігу. По аналогії з індексами збігу, взаємні індекси збігу при зсуві на величину 
 можуть бути обчислені для будь-якої природної мови.
можуть бути обчислені для будь-якої природної мови.
Нехай 
 – стовпець, який отримано в результаті додавання (по модулю
– стовпець, який отримано в результаті додавання (по модулю  ) елемента
) елемента  до кожного елемента стовпця
до кожного елемента стовпця  . За допомогою формули
. За допомогою формули

можуть бути обчислені 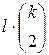 значень
значень 
 . Якщо
. Якщо  , то
, то  близько до взаємного індексу збігу при зсуві на величину
близько до взаємного індексу збігу при зсуві на величину  для природної мови, що використовується, а якщо
для природної мови, що використовується, а якщо  , то
, то  істотно відрізняється від цього індексу, тобто обчислення сеансового ключа зводиться до пошуку розв’язків системи лінійних рівнянь
істотно відрізняється від цього індексу, тобто обчислення сеансового ключа зводиться до пошуку розв’язків системи лінійних рівнянь

 .
.
2. Завдання на проведення лабораторної роботи
Для шифротексту (файл «…Задания ЛР05\CText*.txt», де * − номер варіанту) визначити період сеансового ключа (1-й етап криптоаналізу) та відновити ключ (2-й етап).
Рекомендована література
1. Скобелєв В.Г. Основи захисту інформації. Навчальний посібник. − Донецьк, ДонНТУ, 2006 − 173 с. Ел. вар.
2. Алферов А.П., Зубов А.Ю., Кузьмин А.С., Черемушкин А.В. Основы криптографии. – М.: Гелиос АРВ, 2002. – 480с.
3. Баричев С. Г., Гончаров В.В., Серов Р.Е. Основы современной криптографии: Учеб-ный курс. – М.: Горячая линия – Телеком, 2002. – 175с.
4. Безопасность бизнеса / Под ред. В.А. Динеса. – Саратов: Регион. Приволж. Изд-во «Детская книга», 2002. – 304с.
5. Грибунин В.Г., Оков И.Н., Туринцев И.В. Цифровая стеганография. – М.: СОЛОН-Пресс, 2002. – 272с.
6. Диффи У., Хеллмэн М.Э. Защищенность и имитостойкость: Введение в криптогра-фию // ТИИЭР. – 1979. – Т.67. – № 3. – С.71-109.
7. Иванов М.А. Криптографические методы защиты информации в компьютерных сис-темах и сетях. – М.: КУДИЦ-ОБРАЗ, 2001. – 368с.
8. Масленников М. Е. Практическая криптография. – СПб.: БХВ-Петербург, 2003. – 464с.
9. Молдовян А. А., Молдовян Н.А., Гуц Н.Д., Изотов Б.В. Криптография: скоростные шифры. – СПб.: БХВ-Петербург, 2002. – 496с.
19. Норткат С., Купер М., Фирноу М., Фредерик К. Анализ типовых нарушений в се-тях. – М.: Вильямс, 2001. – 464с.
11. Петраков А. В. Основы практической защиты информации. – М.: Радио и связь, 2000. – 368с.
12. Саломаа А. Криптография с открытым ключом. – М.: Мир, 1996. – 318с.
13. Симонович С.В., Евсеев Г.А., Мураховский В.И. INTERNET: Лаборатория мастера. Работа в сети без проблем. – М.: АСТ-ПРЕСС КНИГА, 2003. – 720с.
14. Столлингс В. Криптография и защита сетей: принципы и практика. – М.: Вильямс, 2001. – 672с.
15. Шеннон К. Э. Теория связи в секретных системах // Шеннон К.Э. Работы по теории информации и кибернетики. – М.: ИЛ, 1963. – С.333-402.
16. Шнайер Б. Секреты и ложь. Безопасность данных в цифровом мире. – СПб.: Питер, 2003. – 368с.
17. Шнайер Б. Прикладная криптология. Протоколы, алгоритмы, исходные тексты на языке СИ. – М.: Триумф, 2003. – 816с.
18. Ященко В.В. Введение в криптографию. – М.: МЦНМО-ЧеРО, 1999. – 272с.




