Лабораторна робота 1
Шифри Полібія, Цезаря, Тритемія, Віженера
1. Опис методів шифрування
1.1. Шифр на основі квадрату Полібія (ІІ вік до н.е.). Символи алфавіту, який застосовується для представлення повідомлення, розміщуються в виді квадратної таблиці 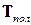 (в загальному випадку така таблиця може бути прямокутною). Шифрування полягає в заміні кожного символу
(в загальному випадку така таблиця може бути прямокутною). Шифрування полягає в заміні кожного символу  повідомлення впорядкованою парою чисел
повідомлення впорядкованою парою чисел  , де
, де 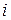 та
та  – номера, відповідно, рядка і стовпця таблиці
– номера, відповідно, рядка і стовпця таблиці 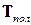 , на перетині яких розташований символ
, на перетині яких розташований символ  . Розшифрування основане на послідовному перегляді шифротексту, виділенні чергової пари чисел
. Розшифрування основане на послідовному перегляді шифротексту, виділенні чергової пари чисел  і її заміні символом
і її заміні символом  , розташованому в таблиці
, розташованому в таблиці 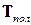 на перетині
на перетині 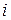 -го рядку і
-го рядку і  -го стовпця.
-го стовпця.
Приклад 1.1. Таблиця 1.1 – варіант квадрату Полібія для російської мови (символ «_» – знак пробілу).
Таблиця 1.1
| А | Б | В | Г | Д | Е | Ж | |
| З | И | Й | К | Л | М | Н | |
| О | П | Р | С | Т | У | Ф | |
| Х | Ц | Ч | Ш | Щ | Ъ | Ы | |
| Ь | Э | Ю | Я | _ | , | ; | |
| : | . | ! | ? | “ | ” | - |
Зашифруємо за допомогою таблиці 1 фразу
МАТЕМАТИКА_–_ЭТО_“ГИМНАСТИКА”_УМА!
Замінимо кожний символ  впорядкованою парою чисел
впорядкованою парою чисел  , де
, де 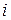 та
та  – відповідно, номер рядка і номер стовпця таблиці 1, на перетині яких розташований символ
– відповідно, номер рядка і номер стовпця таблиці 1, на перетині яких розташований символ  . Отримаємо послідовність чисел:
. Отримаємо послідовність чисел:
Розшифруємо тепер шифротекст
2647553634163315273155331112313511162662,
отриманий за допомогою таблиці 1.
Розіб’ємо отриману послідовність на пари чисел:
(26)(47)(55)(36)(34)(16)(33)(15)(27)(31)(55)(33)(11)(12)(31)(35)
(11)(16)(26)(62).
Замінимо кожну пару чисел  символом, розташованим в таблиці 1 на перетині
символом, розташованим в таблиці 1 на перетині 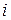 -го рядку і
-го рядку і  -го стовпця. Отримаємо фразу:
-го стовпця. Отримаємо фразу:
МЫ_УСЕРДНО_РАБОТАЕМ!
1.2. Шифр Цезаря (І вік до н.е.). Нехай повідомлення, які передаються, представлені в 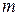 -літерному алфавіті
-літерному алфавіті 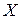 . Побудуємо матрицю
. Побудуємо матрицю  , у якої перший рядок − це символи алфавіту
, у якої перший рядок − це символи алфавіту 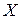 , а другий рядок − це алфавіт
, а другий рядок − це алфавіт 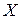 , зсунутий циклічно на
, зсунутий циклічно на  позицій ліворуч. Таким чином, отримаємо підстановку
позицій ліворуч. Таким чином, отримаємо підстановку  елементів множини
елементів множини 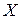 . Позначимо через
. Позначимо через  − символ повідомлення, а через
− символ повідомлення, а через  − символ шифротексту. Шифрування полягає в заміні символу
− символ шифротексту. Шифрування полягає в заміні символу  його образом у підстановці:
його образом у підстановці:  . Ключ шифру − кількість позицій зсуву
. Ключ шифру − кількість позицій зсуву  . Для розшифровки необхідно побудувати підстановку
. Для розшифровки необхідно побудувати підстановку  , і потім замінити символ шифротексту його прообразом:
, і потім замінити символ шифротексту його прообразом:  .
.
Приклад 1.2. Таблиця 1.2 – це підстановка з зсувом на 3 позиції для російського алфавіту, розглянутого в прикладі 1.
Таблиця 1.2
| А | Б | В | Г | Д | Е | Ж | З | И | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ъ | Ы | Ь | Э | Ю | Я | _ | , | ; | : | . | ! | ? | “ | ” | - |
| Г | Д | Е | Ж | З | И | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ъ | Ы | Ь | Э | Ю | Я | _ | , | ; | : | . | ! | ? | “ | ” | - | А | Б | В |
Зашифруємо за допомогою таблиці 1.2 фразу
МАТЕМАТИКА_–_ЭТО_“ГИМНАСТИКА”_УМА!
Отримаємо шифротекст:
ПГХИПГХЛНГ:В:_ХС:АЖЛПРГФХЛНГБ:ЦПГ”
1.3. Шифр на основі таблиці Тритемія (1518 р.). Нехай повідомлення, які передаються, представлені в 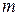 -літерному алфавіті
-літерному алфавіті 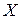 . Таблиця Тритемія – це квадратна таблиця
. Таблиця Тритемія – це квадратна таблиця  розміру
розміру 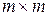 , рядки якої занумеровані числами
, рядки якої занумеровані числами  , а стовпці – елементами алфавіту
, а стовпці – елементами алфавіту 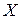 , причому
, причому 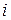 -й рядок
-й рядок  таблиці
таблиці  – це алфавіт
– це алфавіт 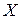 , зсунутий циклічно на
, зсунутий циклічно на 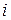 позицій ліворуч. Ясно, що кожна матриця
позицій ліворуч. Ясно, що кожна матриця 
 порядку
порядку  , у якої 1-й рядок – це номера стовпців таблиці
, у якої 1-й рядок – це номера стовпців таблиці  , а 2-й рядок – це
, а 2-й рядок – це 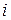 -й рядок таблиці
-й рядок таблиці  , визначає деяку перестановку
, визначає деяку перестановку  елементів множини
елементів множини 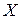 , причому, якщо
, причому, якщо 
 , то перестановки – відмінні.
, то перестановки – відмінні.
Шифрування полягає в заміні  -го символу
-го символу  повідомлення його образом при перестановці
повідомлення його образом при перестановці
 ,
,
тобто при шифруванні 1-го символу використовується 1-й рядок таблиці  , при шифруванні 2-го символу – 2-й рядок таблиці
, при шифруванні 2-го символу – 2-й рядок таблиці  і т.д.
і т.д.
Розшифровка полягає в заміні  -го символу
-го символу  шифротексту його прообразом при перестановці
шифротексту його прообразом при перестановці 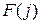 , тобто застосовується перестановка
, тобто застосовується перестановка  . Для цього в таблиці
. Для цього в таблиці  здійснюється пошук
здійснюється пошук  -го символу
-го символу  шифротексту в
шифротексту в  -у рядку, якщо число
-у рядку, якщо число  не кратне числу
не кратне числу 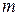 і в
і в 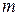 -у рядку, якщо число
-у рядку, якщо число  кратне числу
кратне числу 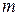 . Далі цей символ замінюється номером стовпця таблиці
. Далі цей символ замінюється номером стовпця таблиці  , в якому він розташований.
, в якому він розташований.
Приклад 1.3. Таблиця 1.3 – це таблиця Тритемія для російського алфавіту, розглянутого в прикладі 1.1.
Зашифруємо за допомогою цієї таблиці фразу
МАТЕМАТИКА_–_ЭТО_“ГИМНАСТИКА”_УМА!
Таблиця 1.3

Отримаємо:
 ,
,  ,
,
 ,
,  ,
,
 ,
,  ,
,
 ,
,  ,
,
 ,
,  ,
,
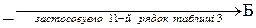 ,
,  ,
,
 ,
, 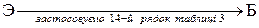 ,
,
 ,
, 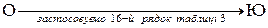 ,
,
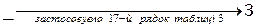 ,
,  ,
,
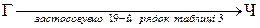 ,
,  ,
,
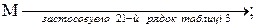 ,
,  ,
,
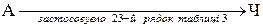 ,
, 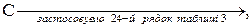 ,
,
 ,
,  ,
,
 ,
,  ,
,
 ,
,  ,
,
 ,
, 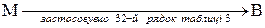 ,
,
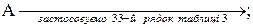 ,
,  .
.
Таким чином, шифротекст має вид:
НВХЙСЖЩРУКГВГБ;ЮЗПЧЬ;.Ч,Б:?ЬЩФИВ;Ь
Зазначимо, що шифр на основі таблиці Тритемія – це нетривіальне узагальнення шифру Цезаря, в якому для шифрування повідомлень, представлених в 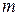 -літерному алфавіті
-літерному алфавіті 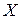 , застосовується лише
, застосовується лише 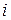 -й рядок таблиці
-й рядок таблиці  . Ясно також, що таблицю
. Ясно також, що таблицю  для
для 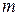 -літерного алфавіту
-літерного алфавіту 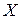 можна розширити до таблиці
можна розширити до таблиці  розміру
розміру  . Для цього достатньо взяти в якості рядків таблиці
. Для цього достатньо взяти в якості рядків таблиці  всі можливі
всі можливі  перестановок
перестановок 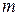 -елементної множини
-елементної множини 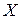 .
.
1.4. Шифри Віженера (XVI вік). Засновані на таблиці Віженера  . В них вперше реалізовано поняття сеансовий ключ, що істотно залежить від повідомлення, яке передається. Таблиця
. В них вперше реалізовано поняття сеансовий ключ, що істотно залежить від повідомлення, яке передається. Таблиця  відрізняється від таблиці Тритемія
відрізняється від таблиці Тритемія  лише тим, що в таблиці
лише тим, що в таблиці  рядки (як і стовпці) занумеровані елементами алфавіту
рядки (як і стовпці) занумеровані елементами алфавіту 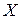 . Нехай повідомлення – це послідовність
. Нехай повідомлення – це послідовність 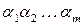 , де
, де 
 . Відправник і адресат заздалегідь домовлялися про пароль, тобто коротку послідовність
. Відправник і адресат заздалегідь домовлялися про пароль, тобто коротку послідовність  символів алфавіту
символів алфавіту 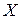 . Відомі такі шифри Віженера.
. Відомі такі шифри Віженера.
1-й шифр Віженера. При шифруванні формуються послідовності  – вихідний текст і
– вихідний текст і 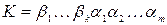 – сеансовий ключ. Представимо ці послідовності в виді
– сеансовий ключ. Представимо ці послідовності в виді
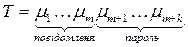 ,
,
 ,
,
де
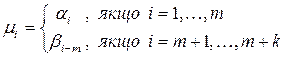 ,
,
 .
.
Шифрування вихідного тексту  здійснюється у відповідності до алгоритму 1.
здійснюється у відповідності до алгоритму 1.
Алгоритм 1.
Крок 1.  .
.
Крок 2.  , де
, де  – символ алфавіту
– символ алфавіту 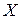 , розташований в таблиці
, розташований в таблиці  на перетині
на перетині 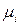 -го рядка и
-го рядка и  -го стовпця,
-го стовпця,  .
.
Крок 3. Якщо  , то перехід до кроку 2, інакше – кінець.
, то перехід до кроку 2, інакше – кінець.
Розшифровка шифротексту  здійснюється згідно з алгоритмом 2.
здійснюється згідно з алгоритмом 2.
Алгоритм 2.
Крок 1.  .
.
Крок 2. В  – у стовпці таблиці
– у стовпці таблиці  здійснюється пошук елементу
здійснюється пошук елементу  .
.
Крок 3.  , де
, де  – номер рядка таблиці
– номер рядка таблиці  , на перетині якого з
, на перетині якого з  -м стовпцем розташований елемент
-м стовпцем розташований елемент  ,
,  .
.
Крок 4. Якщо  , то перехід до кроку 2, інакше – перехід до кроку 5.
, то перехід до кроку 2, інакше – перехід до кроку 5.
Крок 5.  и кінець.
и кінець.
Фінальний відрізок  шифротексту представляє собою «підпис» відправником зашифрованої інформації, якщо під «підписом» розуміти зашифрований пароль. Таким чином, в шифрах Віженера вперше закладений механізм автентифікації (тобто розпізнавання автентичності) як користувача, так і інформації. Така автентифікація здійснюється у відповідності до алгоритму 3.
шифротексту представляє собою «підпис» відправником зашифрованої інформації, якщо під «підписом» розуміти зашифрований пароль. Таким чином, в шифрах Віженера вперше закладений механізм автентифікації (тобто розпізнавання автентичності) як користувача, так і інформації. Така автентифікація здійснюється у відповідності до алгоритму 3.
Алгоритм 3.
Крок 1.  .
.
Крок 2. В  – у стовпці таблиці
– у стовпці таблиці  здійснюється пошук елементу
здійснюється пошук елементу 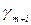 .
.
Крок 3.  , де
, де  – номер рядку таблиці
– номер рядку таблиці  , на перетині якої з
, на перетині якої з  -м стовпцем розташований елемент
-м стовпцем розташований елемент 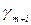 ,
,  .
.
Крок 4. Якщо  , то перехід до кроку 2, інакше – перехід до кроку 5.
, то перехід до кроку 2, інакше – перехід до кроку 5.
Крок 5. Якщо  , то інформацію прийняти і кінець, інакше, інформацію відкинути і кінець.
, то інформацію прийняти і кінець, інакше, інформацію відкинути і кінець.
Алгоритми 2 і 3 можна об’єднати в один алгоритм, тобто при використанні 1-го шифру Віженера автентифікація здійснюється безпосередньо в процесі розшифрування інформації.
2-й шифр Віженера (або шифр з автоключем). Відрізняється від 1-го шифру Віженера тим, що сеансовий ключ має вид 
 , де
, де  – шифротекст, тобто сеансовий ключ
– шифротекст, тобто сеансовий ключ  формується в процесі шифрування вихідного тексту
формується в процесі шифрування вихідного тексту  . Шифрування здійснюється у відповідності до алгоритму 1. Оскільки адресат має пароль
. Шифрування здійснюється у відповідності до алгоритму 1. Оскільки адресат має пароль  (тобто послідовність
(тобто послідовність  ), то він має і сеансовий ключ
), то він має і сеансовий ключ 
 . Розшифровка здійснюється у відповідності до алгоритму 2. Для 2-го шифру Віженера автентифікація здійснюється за допомогою алгоритму 3.
. Розшифровка здійснюється у відповідності до алгоритму 2. Для 2-го шифру Віженера автентифікація здійснюється за допомогою алгоритму 3.
3-й шифр Віженера (або шифр з періодичним ключем). Відрізняється від 1-го шифру Віженера тим, що сеансовий ключ  формується з періодичної (потенційно нескінченої) послідовності
формується з періодичної (потенційно нескінченої) послідовності 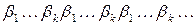 , згідно з правилом:
, згідно з правилом:
 (
( ).
).
Шифрування здійснюється у відповідності до алгоритму 1. Адресат формує сеансовий ключ з паролю  . Розшифровка здійснюється згідно з алгоритмом 2. Для 3-го шифру Віженера автентифікація також здійснюється за алгоритмом 3.
. Розшифровка здійснюється згідно з алгоритмом 2. Для 3-го шифру Віженера автентифікація також здійснюється за алгоритмом 3.
Приклад 1.4. Таблиця 1.4 – це таблиця Віженера для російського алфавіту з лабораторної роботи 1. Зашифруємо з допомогою 1-го шифру Віженера фразу
МАТЕМАТИКА_–_ЭТО_“ГИМНАСТИКА”_УМА!
В якості пароля оберемо слово
ШИФР.
Таким чином, сеансовий ключ  має наступний вид
має наступний вид
ШИФРМАТЕМАТИКА_–_ЭТО_“ГИМНАСТИКА”_УМА!
Для зручності шифрування, запишемо послідовності  і
і  одна під іншою:
одна під іншою:

Таблиця 1.4
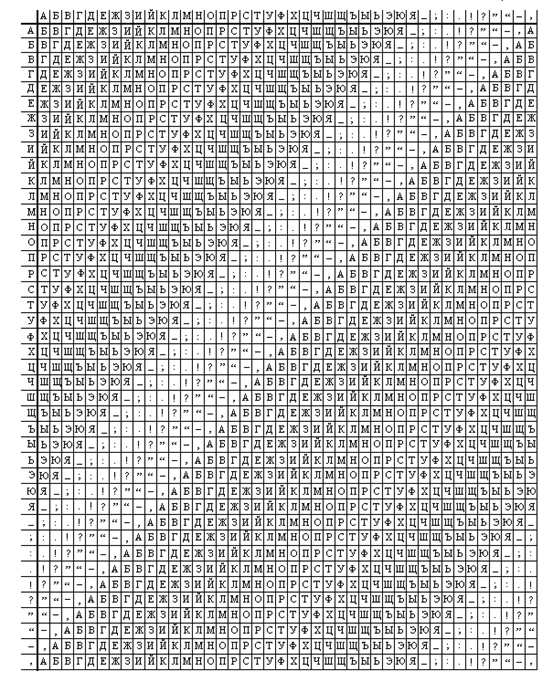
Скористаємось таблицею 1.4. Отримаємо:
 ,
,  ,
, 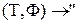 ,
,  ,
,  ,
,
 ,
, 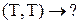 ,
,  ,
,  ,
,  ,
,
 ,
,  ,
, 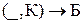 ,
,  ,
,  ,
,
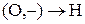 ,
,  ,
,  ,
,  ,
,  ,
,
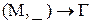 ,
, 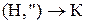 ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,  ,
, 
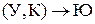 ,
, 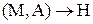 ,
,  ,
, 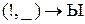 ,
,  ,
,
 ,
,  ,
, 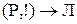 .
.
Таким чином, шифротекст має вид:
?Й“ЦЩБ?ОЧБЙЗБЮЙНЧЫЦЧГЛДЪЯЦЛТП,ЮН“ЫВХХЛ
□
2. Завдання на проведення лабораторної роботи
2.1. Зашифрувати довільну фразу довжиною не менше 16 символів за допомогою шифрів
а) Полібія;
б) Цезаря (значення ключа − номер варіанту);
в) Тритемія.
2.2. Розшифрувати фразу за допомогою таблиці Тритемія. Символи L і R позначають, відповідно, “ та ”. Номер фрази для розшифровки − це номер варіанту за  .
.
Таблиця 1.5
| № | фраза |
| ДТЛЕУЛЛЦЛАУЭЬЬЪВШ_ХФ_МЩОАЬ,!ИФД-ИФЕ!РЬЦЕУР | |
| РКФ_СЖLЩЧОРЬУОЪШЗЦЫ._!.ШБ:И;Д-L?ЧЗЗЛЖRЛЕЮ. | |
| СВФОХ;ТР,ЫУЭЯУЫ.ЗЕ?:Ш!НЖ;ДБЬУВМ?ДФЩЙЛКППН. | |
| ТНСКНСП-ФТЬЮ-ДСЖ:!;.Я,Н_П,БАД_!И,ГБЪЖRКМНЙ | |
| СЗЫЙЧРЗЗ,ЬДСЖДЩЫЕ,ТК_ЫЪ:LРЭАДЕЗ_Д:?ЕГ--И,СГ |
2.3. Зашифрувати довільну фразу довжиною не менше 16 символів за допомогою трьох шифрів Віженера.
2.4. Розшифрувати фразу за допомогою таблиці Віженера. Символи L і R позначають, відповідно, “ та ”.
Таблиця 1.6
| № | ключ | фраза | № шифру |
| ПУСТОТА | RЩЭЕГЙГ-ЛПБХЦЕЭ?Й;ИХ.Ь_НХЪИ,Ц!-Е,_ЙЭ!ВИЧПЬ.ПЫЩИФАЮП | ||
| RЩЭЕГЙГОЯ;Ф!,ЖЪХLLМЯLБЦЕАХИЖЗРRГМЦЗЯСИЙГШ.Б_ШЭХБИФ; | |||
| RЩЭЕГЙГ;ЩХ;ЕИГЫЙЧ?_И;_ФЩХЧ?ЙХНИХЕ_БLФЭШЕФЬЫ:;R_?П:Ф | |||
| МИНЕРАЛ | ЬЬЯШЯУМЖ!ТЪСЫГ;ЬБЩЯ,Л;ЭУТ-;,ГТ?ЖЬЙRЦ!Й..ЧRО!ВВЯЧДКСМЪ | ||
| ЬЬЯШЯУМУГ__:ЬПФП;ИХУШЛ;КЙ;ФПШ:ЭПИЭХ:ЬФГЫВМLЭ_Т-ЛЪГД;Ю | |||
| ЬЬЯШЯУМГЩОНУЙОНФОЧГ;ФГЪ_ЖЬБВЩЙ_Л;ЙСЦВД..ПВСЙЩФЭЙЩТЩОС | |||
| РАСТЕНИЕ | ЭЙЯШЦОФRЭЙХИЩГМВ:_-Л,ФУМЭЦLС.ГЯ!В,LRХAГ-;ФЕДУ_ЙКОФФ | ||
| ЭЙЯШЦОФRДКLЫЯСХИЦАЮ!Ц.-Й:;?ГЩХЛГЩАЬ;В!ВИЪМБИГМХО-ХЗ | |||
| ЭЙЯШЦОФR;БЩХОРЙС:_ИЫRЯЫЖЬ;ШЫИ,Х,ЗЙИЖШЬ,КСМ_.ЖЯЫЛЮЙЧ | |||
| ЖИВОТНОЕ | ЧЙФ;ШЫЧЛЗСТЪИЦЛЖВЯТ!.С.ТЮПЭБЧН.ЪЦБЮБИ!RВLЗЫЯ_ИЗИ, | ||
| ЧЙФ;ШЫЧЛОЪХ,Ы!ЪМЪ,LЬТГСЮГAЙБЙИФLЗБЬЮЫ-О;БИ?;АСЬЖЗ | |||
| ЧЙФ;ШЫЧЛLЩГЦХЦСЖТЧФБЙЦЕЧЩЙОЭЙТСОКЙХБ!ГИ,AПЛС;_ЬФМ | |||
| ЧЕЛОВЕК | ЮООЭХУЩМ,УПЪРЧИ;ЬПЩЯ,Л;Э;Т-Е,И_ЪОМ;RЭБХ,НМЭС-ЬЮТД | ||
| ЮООЭХУЩ!ЕЯЮЭЦ:LЖБГЕЙЩЖLУЦЖХ-LП:ЮФЦСГЫХВЖ.ЛЫ;;СЙ,Ц | |||
| ЮООЭХУЩЭRЬПКИУЪЖЧЭФ:Б_RЭ;ГСЩОЧЪЦРЖЭЭС-ЬЮТДЕЛЧЭЕЛХ | |||
| ДУХОВНЫЙ | ЬЩ;ЭЕУRА-ЖУСЛИЛВ:_-Л,СВЬЧБЧХКУТЯЧЮУЖК:.ЭИЧЭЕЕ:R!ЕЗОLШ | ||
| ЬЩ;ЭЕУRАГЪ,_ОЦLМХР_,Е?,ЭЫЬЧМЩАРВГЕКЖРЮ.С!КЛТЯ.НLЙНЩД, | |||
| ЬЩ;ЭЕУRАХФЭСЛРЬХЦЙМЧ.ЬЭЪКЯМЫЦТВШЦRИИ.БДШ?ШЦЪСТЕЯУЦ.АМ | |||
| АНГЕЛ | Е;ЩФОТЕЯЕЪУLШ.ЭРВ_ХЖЦЧ;;МЩЕ;;-ВЕ.ХБ_ЕЦРАОИЕЫЯТЕ | ||
| Е;ЩФОУУ.ЛRЩЯИОВ!ЦЪ;ГЖНАЖПФЬТЩВЙУ!ЬСЛ:,АГШЬАОЗЮ- | |||
| Е;ЩФОО,НR.ЖЩТИСЛДХШММДУФЧОЬХШ-ЯДХИЪВЬИУLНЗДУПЖЩ |
Лабораторна робота 2
Шифри Кардано і Ардженті, з варіацією






