Задания 61─70. Найти частные производные первого порядка и указанную производную второго порядка от функции:
61. 
| 
|
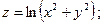
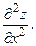
62. 
| 
|
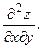
63. 
|
|
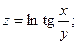
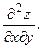
64. z =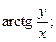 
| 
|
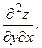
65. 
|
|
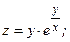
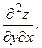
66. 
|
|
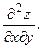
67. 
|
|
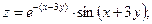
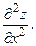
68. 
|
|
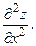
69. 
| 
|
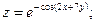
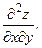
70. 
|
|
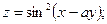
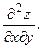
Задания 71─80. Дана функция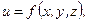 
точка 
и вектор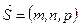 
. Найти:
1) градиент функции в точке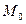 
;
2) производную функции в точке 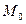по направлению вектора 
.
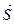71. 
| 
|
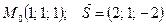
72. 
| 
|
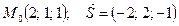
73. 
| 
|
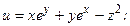
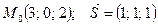
74. 
| 
|
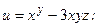
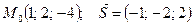
75. 
| 
|
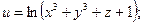
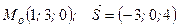
76. 
| 
|
77. 
| 
|
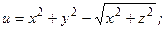
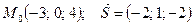
78. 
| 
|
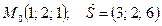
79. 
| 
|
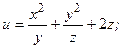
80. 
| 
|
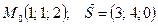
Раздел 6. Неопределенный интеграл
Задания 81─90. Найти неопределенные интегралы. В пунктах 1, 2 выполнить проверку дифференцированием.
81.
1. 
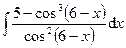
| 2.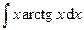 
|
3. 
| 4.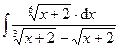 
|
5. 
|
82.
1. 
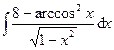
| 2. 
|
3. 
| 4. 
|
5. 
|
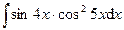
83.
1. 
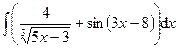
| 2.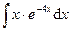 
|
3. 
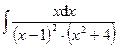
| 4.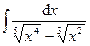 
|
5. 
|
84.
1. 
|
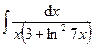
2. 
|
3. 
|
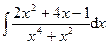
4. 
|
5. 
|
85.
1. 
|
2. 
|
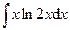
3. 
|
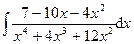
4. 
|
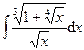
5. 
|
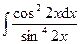
86.
1. 
|
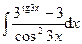
2. 
|
3. 
|
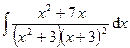
4. 
|
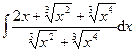
5. 
|
87.
1. 
|
2. 
|
3. 
|
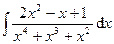
4. 
|
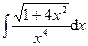
5. 
|
88.
1. 
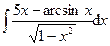
| 2.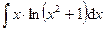 
|
3. 
|
4. 
|
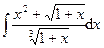
5. 
|
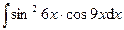
89.
1. 
| 2.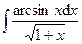 
|
3. 
|
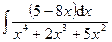
4. 
|
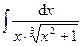
5. 
|
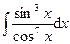
90.
1. 
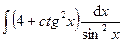
| 2.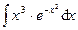 
|
3. 
|
4. 
|
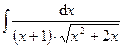
5. 
|
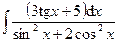
Раздел 7. Определенный интеграл
91. Вычислить площадь плоской фигуры, ограниченной линиями 
92. Вычислить объем тела, полученного вращением вокруг оси oy фигуры, ограниченной линиями 
93. Найти длину кривой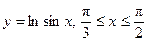 
.
94. Вычислить площадь плоской фигуры, ограниченной линиями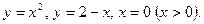 
95. Вычислить объем тела, полученного вращением вокруг оси ох фигуры, ограниченной линиями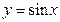 
(одной полуволны),
у = 0.
96. Найти длину кривой 
97. Вычислить площадь плоской фигуры, ограниченной линиями 
.
98. Вычислить объем тела, полученного вращением вокруг оси ох фигуры, ограниченной линиями 
99. Найти длину кривой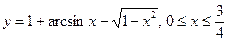 
.
100. Вычислить площадь плоской фигуры, ограниченной линиями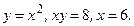 
Раздел 8. Дифференциальные уравнения
Задания 101─110. Найти частное решение дифференциального уравнения первого порядка, удовлетворяющее условию 
.
101. 
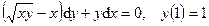
102. 
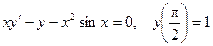
103. 
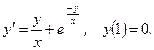
104. 
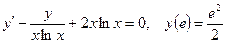
105. 
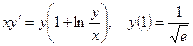
106. 
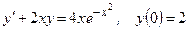
107. 
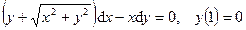
108. 
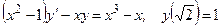
109. 
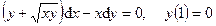
110. 
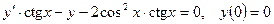
Задания 111─120. Найти общее решение дифференциального уравнения.
111. 
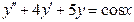
112. 
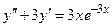
113. 
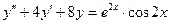
114. 
115. 
116. 
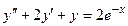
117. 
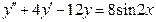
118. 
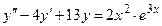
119. 
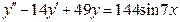
120. 
Раздел 9. Кратные, криволинейные
и поверхностные интегралы
Задания 121–130. Изменить порядок интегрирования в двойном интеграле.
121. 
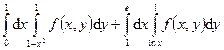
122. 
123. 
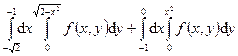
124. 
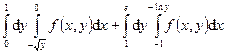
125. 
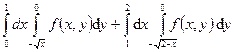
126. 
127. 
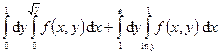
128. 
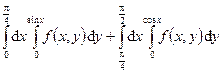
129. 
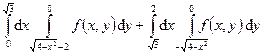
130. 
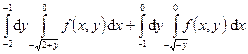
Задания 131─140. Вычислить объем тела, ограниченного данными поверхностями. Сделать чертежи данного тела и его проекции на плоскость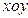 
.
131. 
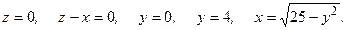
132. 
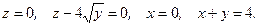
133. 
134. 
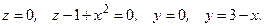
135. 
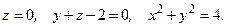
136. 
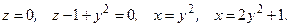
137. 
138. 
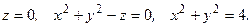
139. 
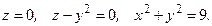
140. 
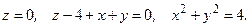
Раздел 10. Элементы теории поля
Задания 141─150. Вычислить работу силы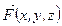 
при перемещении материальной точки вдоль линии L от точки А до точки В.
141. 
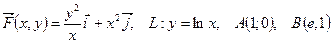
142. 
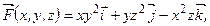
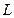– отрезок прямой,
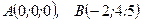
143. 
,
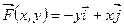дуга астроиды 
, 
144. 
145. 
отрезок прямой,
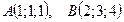
146. 
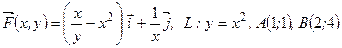
147. 
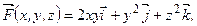L – дуга одного витка винтовой линии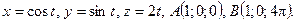 
148. 
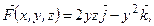L – ломаная ACB,
.
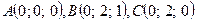149. 
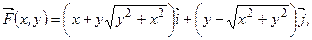L – дуга окружности 
.
150. 
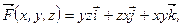L – дуга винтовой линии 
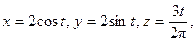A – точка пересечения линии с плоскостью z = 0, В – точка пересечения линии с плоскостью z = 3.
Задания 151–160. Проверить, является ли векторное поле 
соленоидальным и потенциальным. В случае потенциальности поля найти его потенциал.
151. 
152. 
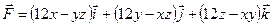
153. 
154. 
155. 
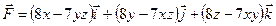
156. 
157. 
158. 
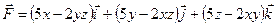
159. 
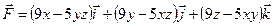
160. 
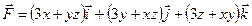
Раздел 11. Ряды
Задания 161–170. Записать общий член ряда и исследовать ряд на сходимость.
161. 
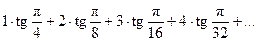
162. 
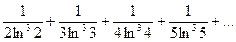
163. 
164. 
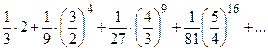
165. 
166. 
167. 
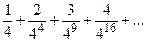
168. 
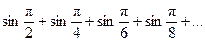
169. 
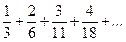
170. 
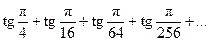
Задания 171–180. Найти область сходимости следующих рядов:
171. 
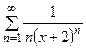
| 172.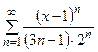 
|
173. 
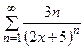
| 174.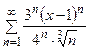 
|
175. 
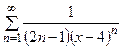
| 176.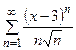 
|
177. 
| 178.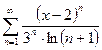 
|
179. 
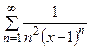
| 180. 
|
