
Задания 1─10. 1. Исследовать систему линейных уравнений.
2. В случае совместности, решить систему методом Гаусса.
1. 
| 2. 
|
3. 
| 4. 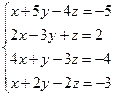
|
5. 
| 6. 
|
7. 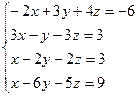
| 8. 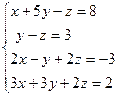
|
9. 
| 10. 
|
Задания 11─20. Даны векторы
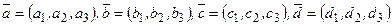
в некотором базисе. Показать, что векторы 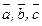 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора  в этом базисе. Систему линейных уравнений решить по формулам Крамера.
в этом базисе. Систему линейных уравнений решить по формулам Крамера.
11. 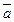 = (1; 2; 3),
= (1; 2; 3), 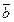 = (-1; 3; 2),
= (-1; 3; 2),  = (7; -3; 5),
= (7; -3; 5),
 = (6; 10; 17).
= (6; 10; 17).
12. 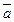 = (4; 7; 8),
= (4; 7; 8), 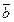 = (9; 1; 3),
= (9; 1; 3),  = (2; -4; 1),
= (2; -4; 1),
 = (1; -13; -13).
= (1; -13; -13).
13. 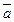 = (8; 2; 3),
= (8; 2; 3), 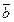 = (4; 6; 10),
= (4; 6; 10),  = (3; -2; 1),
= (3; -2; 1),
 = (7; 4; 11).
= (7; 4; 11).
14. 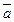 = (10; 3; 1),
= (10; 3; 1), 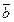 = (1; 4; 2),
= (1; 4; 2),  = (3; 9; 2),
= (3; 9; 2),
 = (19; 30; 7).
= (19; 30; 7).
15. 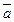 = (2; 4; 1),
= (2; 4; 1), 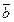 = (1; 3; 6),
= (1; 3; 6),  = (5; 3; 1),
= (5; 3; 1),
 = (24; 20; 6).
= (24; 20; 6).
16. 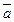 = (1; 7; 3),
= (1; 7; 3), 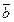 = (3; 4; 2),
= (3; 4; 2),  = (4; 8; 5),
= (4; 8; 5),
 = (7; 32; 14).
= (7; 32; 14).
17. 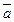 = (1; -2; 3),
= (1; -2; 3), 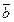 = (4; 7; 2),
= (4; 7; 2),  = (6; 4; 2),
= (6; 4; 2),
 = (14; 18; 6).
= (14; 18; 6). 
18. 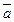 = (1; 4; 3),
= (1; 4; 3), 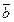 = (6; 8; 5),
= (6; 8; 5),  = (3; 1; 4),
= (3; 1; 4),
 = (21; 18; 33).
= (21; 18; 33).
19. 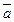 = (2; 7; 3),
= (2; 7; 3), 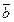 = (3; 1; 8),
= (3; 1; 8),  = (2; -7; 4),
= (2; -7; 4),
 = (16; 14; 27).
= (16; 14; 27).
20. 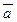 = (7; 2; 1),
= (7; 2; 1), 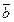 = (4; 3; 5),
= (4; 3; 5),  = (3; 4; -2),
= (3; 4; -2),
 = (2; -5; -13).
= (2; -5; -13).
Раздел 2. Аналитическая геометрия
Задания 21─30. Даны координаты вершин пирамиды А1, А2, А3, А4. Найти:
1) площадь грани А1А2А3;
2) объем пирамиды;
3) уравнения прямой А1А2;
4) уравнение плоскости А1А2А3;
5) уравнение высоты А4D, опущенной из вершины А4 на грань А1А2А3;
6) длину высоты А4D;
7) координаты точки пересечения высоты А4D с плоскостью А1А2А3.
21. А1 (4; 2; 5), А2 (0; 7; 2), А3 (0; 2; 7), А4 (1; 5; 0).
22. А1 (4; 4; 10), А2 (4; 10; 2), А3 (2; 8; 4), А4 (9; 6; 4).
23. А1 (4; 6; 5), А2 (6; 9; 4), А3 (2; 10; 10), А4 (7; 5; 9).
24. А1 (3; 5; 4), А2 (8; 7; 4), А3 (5; 10; 4), А4 (4; 7; 8).
25. А1 (10; 6; 6), А2 (- 2; 8; 2), А3 (6; 8; 9), А4 (7; 10; 3).
26. А1 (1; 8; 2), А2 (5; 2; 6), А3 (5; 7; 4), А4 (4; 10; 9).
27. А1 (6; 6; 5), А2 (4; 9; 5), А3 (4; 6; 11), А4 (6; 9; 3).
28. А1 (7; 2; 2), А2 (5; 7; 7), А3 (5; 3; 1), А4 (2; 3; 7).
29. А1 (8; 6; 4), А2 (10; 5; 5), А3 (5; 6; 8), А4 (8; 10; 7).
30. А1 (7; 7; 3), А2 (6; 5; 8), А3 (3; 5; 8), А4 (8; 4; 1).
31. Прямые 2 х + у – 1 = 0 и 4 х – у – 11 = 0 являются сторонами треугольника, а точка Р (1; 2) – точкой пересечения третьей стороны с высотой, опущенной на нее. Составить уравнение третьей стороны. Сделать чертеж.
32. Прямая 5 х - 3 у + 4 = 0 является одной из сторон треугольника, а прямые 4 х - 3 у + 2 = 0 и 7 х + 2 у – 13 = 0 его высотами. Составить уравнения двух других сторон треугольника. Сделать чертеж.
33. Точки А (3; -1) и В (4; 0) являются вершинами треугольника, а точка D (2; 1) - точкой пересечения его медиан. Составить уравнение высоты, опущенной из третьей вершины. Сделать чертеж.
34. Прямые 3 х - 4 у + 17 = 0 и 4 х – у – 12 = 0 являются сторонами параллелограмма, а точка Р (2; 7) – точкой пересечения его диагоналей. Составить уравнения двух других сторон параллелограмма. Сделать чертеж.
35. Прямые х - 2 у + 10 = 0 и 7 х + у - 5 = 0 являются сторонами треугольника, а точка D (1; 3) ─ точкой пересечения его медиан. Составить уравнение третьей стороны. Сделать чертеж.
36. Прямые 5 х - 3 у + 14 = 0 и 5 х - 3 у – 20 = 0 являются сторонами ромба, а прямая х - 4 у – 4 = 0 – его диагональю. Составить уравнения двух других сторон ромба. Сделать чертеж.
37. На прямой 4 х + 3 у – 6 = 0 найти точку, равноудаленную от точек А (1; 2) и В (- 1; - 4). Сделать чертеж.
38. Найти координаты точки, симметричной точке А (5;2) относительно прямой х + 3 у – 1 = 0. Сделать чертеж.
39. Прямые х - 3 у + 6 = 0 и 3 х + у – 12 = 0 являются сторонами прямоугольника, а точка Р (7; 2) – точкой пересечения его диагоналей. Составить уравнения двух других сторон прямоугольника. Сделать чертеж.
40. Точки А (4;5) и С (2; - 1) являются двумя противоположными вершинами ромба, а прямая х – у + 1 = 0 – одной из его сторон. Составить уравнения остальных сторон ромба. Сделать чертеж.
Раздел 3. Введение в математический анализ
Задания 41─50. Вычислить пределы.
41.
1. 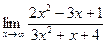
|
2. 
|
3. 
|
4. 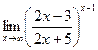
|
5. 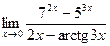
| |
42.
1. 
|
2. 
|
3. 
| 4. 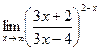
|
5. 
| |
43.
1. 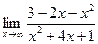
|
2. 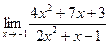
|
3. 
| 4.  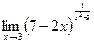
|
5. 
| |
44.
1. 
|
2.  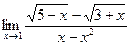
|
3. 
|
4. 
|
5. 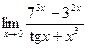
| |
45.
1. 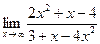
|
2. 
|
3. 
|
4. 
|
5. 
| |
46.
1. 
|
2. 
|
3. 
|
4. 
|
5. 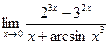
| |
47.
1. 
|
2. 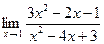
|
3. 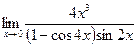
|
4. 
|
5. 
| |
48.
1. 
|
2. 
|
3. 
|
4. 
|
5. 
| |
49.
1. 
|
2. 
|
3. 
|
4. 
|
5. 
| |
50.
1. 
|
2. 
|
3. 
|
4. 
|
5. 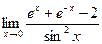
|
Раздел 4. Дифференциальное исчисление
Функции одной переменной
Задания 51─60. Найти производные 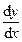 следующих функций:
следующих функций:
| 51. | |
1. 
| 2. 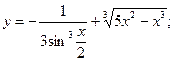
|
3. 
|
4. 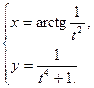
|
52.
1. 
|
2. 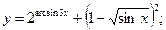
|
3. 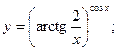
|
4. 
|
53.
1. 
| 2. 
|
3. 
| 4. 
|
54.
1. 
| 2. 
|
3. 
|
4. 
|
55.
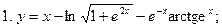
| |
2.  3.
3. 
|
4. 
|
56.

| |
2.  3.
3. 
|
4. 
|
57.
1. 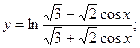
|
2. 
|
3. 
| 4. 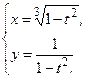
|
58.
1. 
| |
2. 
| |
3. 
| 4. 
|
59.
1. 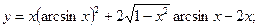
| |
2. 
| |
3. 
| 4. 
|
60.
1. 
| |
2. 
| |
3. 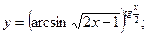
|
4. 
|






