Линейная краевая задача имеет вид:
 .
.  , при
, при 

 . Решение задачи проводится в следующей последовательности:
. Решение задачи проводится в следующей последовательности:
1. Определение сетки.
Отрезок [a,b] делится на 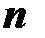 частей:
частей:

| 
| … | 
| … | 
| 
| 
| |||||||

| 
| … | 
| … | 
| 
| 
| |||||||
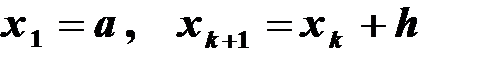 ,
,  ,
, 
2. Определение сеточной функции  :
:

| 
| 
| … | 
|

| 
| 
| … | 
|
3. Аппроксимация уравнения:
Для каждой узловой точки  заменяем функции и производные в уравнениях 6.9-6.10 конечноразностными аналогами:
заменяем функции и производные в уравнениях 6.9-6.10 конечноразностными аналогами:


 т.е.
т.е. 


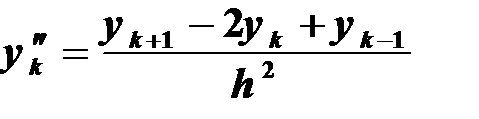 (6.11)
(6.11)

 т.е.
т.е. 
Получаем ситему  линейных алгебраических уравнений для определения
линейных алгебраических уравнений для определения 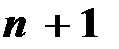 неизвестных величин
неизвестных величин  .
.
Задачи Коши для обыкновенных дифференциальных уравнений.
Метод Эйлера. Одним из простейших разностных методов решения обыкновенного дифференциального уравнения является метод Эйлера. Пусть требуется решить задачу Коши для уравнения первого порядка:  , на отрезке
, на отрезке  . На данном отрезке выбираем некоторую совокупность точек
. На данном отрезке выбираем некоторую совокупность точек  с равностоящими узлами, т.е.
с равностоящими узлами, т.е. 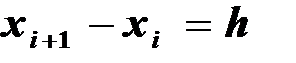 .Конечно-разностная аппроксимация прозводной
.Конечно-разностная аппроксимация прозводной  Так как
Так как  , получаем формулу Эйлера
, получаем формулу Эйлера  ,
,  , с помощью которой значение сеточной функции
, с помощью которой значение сеточной функции  в любом узле
в любом узле  вычисляется по ее значению
вычисляется по ее значению  в предыдущем узле
в предыдущем узле 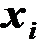 . На каждом шаге погрешность имеет порядок
. На каждом шаге погрешность имеет порядок  . В конце интервала погрешность
. В конце интервала погрешность 

 , т.е. метод Эйлера имеет первый порядок точности. На рис. 6.1 дана геометрическая интерпретация метода Эйлера.
, т.е. метод Эйлера имеет первый порядок точности. На рис. 6.1 дана геометрическая интерпретация метода Эйлера.
Модифицированный метод Эйлера. Модифицированный метод Эйлера позволяет уменьшить погрешность на каждом шаге до величины 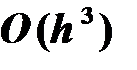 вместо
вместо 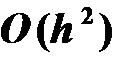 в обычном методе. Запишем разложение функции в ряд Тейлора в виде:
в обычном методе. Запишем разложение функции в ряд Тейлора в виде:  . Аппроксимируем вторую производную с помощью отношения конечных разностей:
. Аппроксимируем вторую производную с помощью отношения конечных разностей:  Подставляя это соотношение в и пренебрегая членами порядка
Подставляя это соотношение в и пренебрегая членами порядка 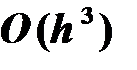 , получаем:
, получаем:  . Полученная схема является неявной, поскольку искомое значение
. Полученная схема является неявной, поскольку искомое значение 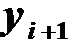 входит в обе части соотношения, но можно построить приближенное решение с использованием двух итераций. Сначала по формуле Эйлера вычисляют первое приближение
входит в обе части соотношения, но можно построить приближенное решение с использованием двух итераций. Сначала по формуле Эйлера вычисляют первое приближение 
 . Затем находится уточненное окончательное значение
. Затем находится уточненное окончательное значение  . Такая схема решения называется модифицированным методом Эйлера и имеет второй порядок точности.
. Такая схема решения называется модифицированным методом Эйлера и имеет второй порядок точности.
Метод Рунге-Кутта. Формулы можно представить в виде  где
где  Такая формулировка модифицированного метода Эйлера представляет собой метод Рунге-Кутта второго порядка. На основе метода Рунге-Кутта могут быть построены разностные схемы разного порядка точности. Наиболее употребительной является следующая схема четвертого порядка:
Такая формулировка модифицированного метода Эйлера представляет собой метод Рунге-Кутта второго порядка. На основе метода Рунге-Кутта могут быть построены разностные схемы разного порядка точности. Наиболее употребительной является следующая схема четвертого порядка:  где
где  . Таким образом, метод Рунге-Кутта требует на каждом шаге четырехкратного вычисления правой части уравнения. Однако это окупается повышенной точностью, что дает возможность проводить счет с относительно большим шагом.
. Таким образом, метод Рунге-Кутта требует на каждом шаге четырехкратного вычисления правой части уравнения. Однако это окупается повышенной точностью, что дает возможность проводить счет с относительно большим шагом.






