Уравнение Менделеева - Клапейрона является уравнением состояния идеального газа и довольно точно описывает поведение реальных газов при небольшой плотности, т.е. достаточно низком давлении и высокой температуре (
).
При понижении температуры и увеличении давления, плотность газа увеличивается, а расстояние между его молекулами уменьшается, поэтому пренебрегать их объёмом и взаимо-
Рис. 23 действием мы не можем.
Силы взаимного притяжения между молекулами направлены внутрь газа, т. е. в сторону наибольшего окружения периферийных молекул (рис.23).
Действие этих сил подобно наличию некоторого добавочного давления на газ, называемого внутренним.
В связи с тем, что молекулы газа занимают конечные размеры, они занимают суммарный объём V/. Поэтому объём, предоставленный для передвижений молекулам, будет меньше на величину V'. Таким образом, для описания состояния реальных газов необходимо сделать две поправки:
а) на дополнительное давление, обусловленное взаимодействием молекул;
б) на уменьшение объёма, в связи с учётом размеров самих молекул.
Возьмём за основу уравнение состояния идеального газа и, внеся в него соответствующие поправки, получим уравнение состояния реального газа. Для одного моля газа имеем
.
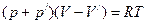Внесённые поправки были впервые рассчитаны и предложены Ван-дер-Ваальсом (гол.)
; 
,
где а и в – постоянные Ван-дер-Ваальса.
Уравнение Ван-дер-Ваальса для одного моля реального газа имеет вид:
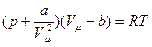. (26)
Учитывая, что 
и, умножив обе части уравнения на 
, получим уравнение Ван-дер-Ваальса для любой массы газа: 
. (27)
Полученные нами уравнения имеют третью степень относительно V, например, для одного моля после преобразования, оно будет иметь вид:
0.
Это означает, что оно может иметь либо три действительных, либо один действительный и два мнимых корня, при чём физический смысл имеют только действительные корни.
Эти особенности уравнения состояния нашли своё отражение в графиках зависимости p (Vm), называемых кривыми Ван-дер-Ваальса (рис. 24).
Заметим, что при некоторой температуре лишь одна точка перегиба. Она называется критической.
Параметры (рк, Vк, Tк), соответствующие критической точке, также называют критическими
, 
, 
.
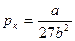Рис. 24 Рис. 25
Изотермы реального газа (рис.24) несколько отличаются от экспериментальных изотерм (рис.25), характерной особенностью которых является наличие горизонтальных участков А 1 В 1, А 2 В 2 и т. д. Эти участки соответствуют равновесным состояниям между жидкостью и её насыщенным паром.
Проводя сравнительный анализ расчётных и экспериментальных кривых, отметим, что при достаточно высоких температурах (T > Tкр) реальные изотермы напоминают изотермы идеального газа. Этим объясняется возможность расчётов параметров реальных газов с помощью выражений для идеального газа.
