В результате теплового движения молекулы веществ (в первую очередь газов) перемешиваются. При перемешивании между ними происходит взаимный обмен местоположением, энергией или импульсом.
При этом если в среде имеются неоднородности плотности, температуры или скорости поступательного движения молекул, то в ней возникают процессы, стремящиеся устранить эти неоднородности. Эти процессы обусловлены тепловым движением молекул и объединены общим названием – явления переноса.
Явления переноса – это необратимые процессы в неравновесных термодинамических системах, при которых происходит перенос массы, теплоты или импульса.
К явлениям переноса относятся диффузия, теплопроводность и вязкость.
Диффузия – самопроизвольное выравнивание плотности (концентрации) вещества посредством теплового движения его молекул.
Пусть в некотором объёме газа имеет место неоднородность плотности (неодинаковая плотность в различных частях объёма). В результате теплового движения молекулы перемещаются во всевозможных направлениях. Однако, имеющаяся разница в плотности приводит к тому, что количество молекул, перемещённых из области, с более высокой плотностью будет больше.
Т. е. возникает поток вещества, а точнее его массы, направленный в сторону убывания его плотности
.
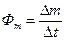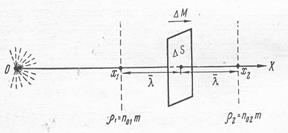
Выберем некоторое направление ОХ, в котором плотность вещества изменяется от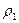 
до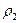 
(рис.6).
Выделим в плоскости, перпендикулярной направлению ОХ контур площадью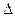 
S и поместим источник
Рис. 6 распространения вещества в точку О.
Распространение вещества подразумевает перенос через выделенный контур некоторой массы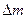 
.
Быстроту изменения плотности вещества характеризует градиент плотности
.
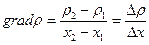Процесс диффузии характеризуется законом Фика (Адольф Фик нем. 1855г.):
- плотность потока массы пропорциональна градиенту плотности вещества
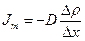, (13)
где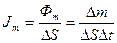 
- плотность потока массы, 
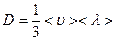– коэффициент диффузии:
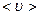- средняя скорость молекул, 
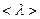средняя длина свободного пробега молекул.
Средней называется скорость, определяемая как среднее арифметическое скоростей всех молекул
.
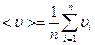Для определения средней скорости в молекулярной физике используется формула
.
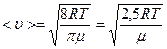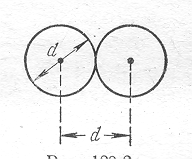
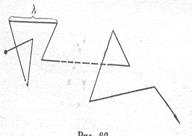Путь, который молекула проходит между двумя последующими соударениями, называется средней длиной свободного пробега 
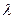(рис. 7)
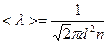, (14)
где n – концентрация молекул (кол-во в единице объёма), d – эффективный диаметр – наименьшее расстояние, на которое сближаются центры молекул при их столкновении (рис.8).
Рис. 7 Рис. 8 Длину свободного пробега 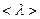можно выразить через давление и температуру, воспользовавшись уравнением р = nkT
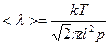. (15)
Коэффициент диффузии – величина, численно равная плотности потока массы вещества при единичном градиенте плотности.
Наиболее широко известные проявления диффузии являются: окрашивание растворов, распространение запахов, однородность смеси газов в атмосфере, газообмен в лёгких, обмен веществ в пищеварительной системе и др.
Пусть в некотором объёме пространства кинетическая энергия молекул, а, значит, температура различна (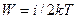
). В результате теплового движения молекулы обмениваются энергией друг с другом, в результате чего возникает поток энергии 
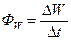, направленный в сторону с меньшей температурой.
Процесс передачи внутренней энергии (теплоты) в веществе посредством теплового движения его молекул называется теплопроводностью.
Выберем некоторое направление ОХ, в котором температура вещества изменяется от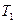 
до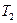 
(рис.9).
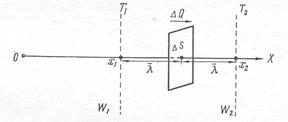Выделим в этом объёме некоторый контур площадью 
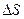, перпендикулярный выбранному ранее направлению изменения температуры ОХ.
Поток теплоты, прошедший сквозь выделенный контур, обозначим как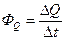 
.
Поток теплоты, приходящийся на единицу площади контура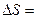 
1м2, представляет собой плотность этого
Рис. 9 потока JQ: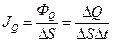 
.
Теплопроводность подчиняется закону Фурье (Жан Фурье фр. 1822г.): плотность потока теплоты через некоторый контур пропорционален градиенту температуры, созданному по разные стороны от этого контура
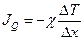, (16)
где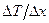 
- градиент плотности вещества; 
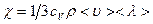- коэффициент теплопроводности вещества, cV = 
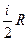– удельная теплоёмкость при постоянном давлении, 
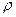- плотность, 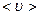- средняя скорость, < 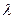> средняя длина свободного пробега молекул.
Коэффициент теплопроводности – величина, численно равная плотности потока теплоты при единичном градиенте температуры. Он характеризует способность вещества проводить теплоту.
Знак (-) указывает на то, что теплота переносится в сторону убывания температуры.
Исходя из этих данных, можно сделать вывод о том, на сколько важно учитывать теплопроводные свойства материалов в различных отраслях жизнедеятельности – строительстве, медицине, промышленном производстве и др.
Теплопередача значительно ускоряется при взаимном перемешивании слоёв жидкости или газа, т.е. при конвекции.
Конвекционные потоки можно наблюдать, например, над пламенем костра или кипящей жидкостью. Посредством конвекции происходит также выравнивание температуры в обогреваемых помещениях (рис. 10 а ).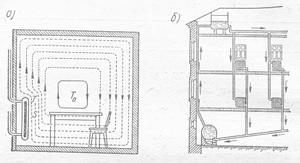 
Принудительная конвекция или циркуляция воды используется в устройстве водяного центрального отопления домов (рис. 10 б).
Ещё одним видом теплообмена является теп-
а) б) ловое излучение, осуществляемое посредством
Рис. 10 электромагнитного поля.
Дело в том, что всякое тело с температурой отличной от абсолютного нуля, способно к излучению энергии в виде электромагнитных волн. Наиболее значимым видом этого излучения в природе являются солнечный свет и теплота. На том же принципе работает и СВЧ – нагревательная бытовая аппаратура, а также физиотерапевтическое медицинское оборудование.
При изучении силы трения, отмечалось, что трение между частями одного и того же тела называется внутренним.
В качестве этих частей, обычно выступают слои жидкости или газа.
Деление жидкости на слои является условным, т.к. оно обусловлено не фактическим их существованием, а разницей в скорости поступательного движения молекул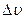 
.
Предположим, что разница в скорости поступательного движения
слоёв составляет не более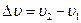 
(рис.11).
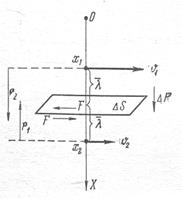Рис. 11 Движение каждой молекулы потока жидкости (или газа) можно представить в виде двух составляющих – поступательной, обусловленной течением жидкости и хаотической, обусловленной тепловым движением молекул.
Средняя скорость хаотического движения молекул многократно превышает поступательную составляющую, что неизбежно приводит
к тому, что молекулы переходят из одного слоя в другой.
При соударениях молекулы обмениваются друг с другом своими импульсами.
В результате, импульс молекул с большей скоростью передаётся молекулам с меньшей скоростью поступательного движения (рис.11).
Другими словами более быстрые слои замедляются, как если бы
Рис. 12 к ним была приложена тормозящая сила – сила внутреннего трения:
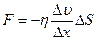(17).
Взаимодействие двух слоёв жидкости (согласно 2 закону Ньютона) можно рассматривать как процесс, при котором от одного слоя к другому за единицу времени передаётся импульс, равный по модулю действующей силе – силе внутреннего трения
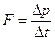(18).
Тогда, решая систему уравнений (1) и (2), имеем:
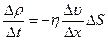, или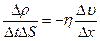 
.
Окончательно получаем выражения закона Ньютона для внутреннего трения: - плотность потока импульса, перенесённого через некоторый контур пропорциональна градиенту скорости слоёв
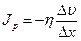, (19)
где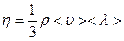 
- коэффициент вязкости вещества – величина, равная плотности потока импульса, возникающего при единичном градиенте скорости.
Знак (-) указывает на то, что импульс передаётся в направлении убывания скорости слоёв.
Вязкость жидкостей с ростом их температуры увеличивается.
При движении тел в вязких средах между слоями, вовлечёнными ими в движение, также возникают силы внутреннего трения.
Силу внутреннего трения, возникающую при движении тел шарообразной формы в средах, обладающих вязкостью, определяют согласно закону Стокса
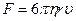, (20)
где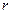 
- радиус тела, 
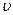- установившаяся скорость движения.
Жидкое состояние вещества характеризуется значительно меньшим расстоянием между молекулами, чем газообразное. Силы притяжения между молекулами становятся значительными, но не достаточными для того, чтобы жёстко удерживать молекулы друг возле друга.
Поэтому молекулы жидкости в основном совершают лишь местные перемещения (перескакивают) из одного временного положения в другое. Среднее время оседлой жизни молекул составляет интервал порядка 10-11 с. В силу сказанного можно заключить, что жидкость занимает промежуточное положение между газами и твёрдыми телами. А именно – сохраняет объём, как твёрдые тела, и не сохраняет форму, подобно газам. Способность молекул жидкости перемещаться по занимаемому объёму приводит к возникновению явлений, присущих только жидкостям. К числу таковых относятся текучесть, вязкость и поверхностное натяжение.
Поверхностным натяжением называется напряжённое состояние поверхности жидкости, обусловленное дополнительными силами притяжения между молекулами поверхностного слоя.
Поверхностным является слой жидкости, толщиной, равной радиусу молекулярного действия r (рис.13 а).
Рис. 13 Радиусом молекулярного действия называется расстояние, на котором силы притяжения молекул становятся пренебрежимо малыми.
Радиус молекулярного действия не превышает нескольких эффективных диаметров молекул dэф.
Рассмотрим причины возникновения поверхностного натяжения. Для этого сравним силы, действующие со стороны окружающих молекул на молекулу, находящуюся внутри жидкости и на её поверхности.
На молекулу в глубине жидкости эти силы действуют равномерно со всех сторон и взаимно компенсируются.
Действие на молекулу поверхностного слоя носит ассиметричный характер, поскольку притяжение со стороны молекул жидкости значительно превосходит воздействие со стороны молекул газа, граничащего с жидкостью.
Складывая векторы сил, действующих на молекулу А поверхности жидкости, получим результирующую fп(n-нормаль), направленную внутрь жидкости (рис.13б).
Стремление молекул из поверхности внутрь жидкости приводит к возникновению
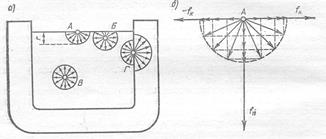
дополнительных касательных к поверхности сил fк, обуславливающих поверхностное натяжение. Суммарное действие этих сил характеризуется силой поверхностного натяжения. Для количественного определения сил поверхностного натяжения на поверхности жидкости выделяют контур из молекул, ограничивающих эту поверхность (рис.14).
Здесь Fп – сила поверхностного натяжения, F/ - сила сцепления молекул жидкости с молекулами вещества Рис. 14 стенок сосуда. Сила поверхностного натяжения пропорциональна длине контура, ограничивающего данную поверхность
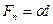, (21)
где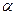 
- коэффициент поверхностного натяжения (КПН).
КПН – величина, численно равная силе поверхностного натяжения, приходящейся на единицу длины контура, ограничивающего данную поверхность. КПН зависит от рода жидкости и её температуры.
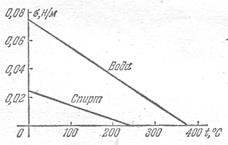При повышении температуры силы притяжения между молекулами уменьшаются, соответственно ослабевает и поверхностное натяжение жидкости (рис.15).
Рассмотрим энергетическую сторону поверхностного натяжения. Силы поверхностного натяжения Fп (рис.6) по своему действию схожи с силами тяготения. И подобно тому, как нужно совершить работу, чтобы поднять тело на высоту h, внутренним молекулам жидкости также нужно совершить работу, чтобы подняться на поверхность. Это означает, что молекулы поверхностного слоя обладают дополнительной по сравнению с другими молекулами потенциальной энергией. Эта энергия называется поверхностной, или энергией поверхност-
Рис. 15 ного слоя и определяется из уравнения
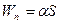, (22)
где S – площадь поверхности жидкости, 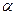- КПН.
Поскольку система, предоставленная сама себе, стремится к минимуму своей потенциальной энергии, жидкость в свободном состоянии стремиться принять такую форму, при которой её поверхность будет минимальной. Например, капля жидкости или мыльный пузырь принимают шарообразную форму. Эти же причины заставляют жидкость изменять свою форму вблизи стенок сосуда, в котором она находится (рис.16).
При взаимодействии молекул жидкости с молекулами сосуда возможны два варианта распределения сил взаимодействия.
а) Силы притяжения молекул жидкости к молекулам твёрдого тела больше сил взаимодействия между молекулами самой жидкости.
В этом случае частицы жидкости пристают (прилипают) к стенке сосуда.
Это явление называют смачиванием, а жидкость – смачивающей.
б) Силы взаимодействия молекул жидкости превосходят силы притяжения со стороны молекул твёрдого тела – не смачивание, жидкость соответственно называют не смачивающей.
Рассмотрим силы, действующие на молекулу поверхности смачивающей жидкости вблизи стенки сосуда (рис.4а)
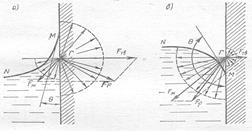
Результирующую силу FР, действующую па молекулу Г, можно выразить путём векторного сложения сил притяжения со стороны молекул твёрдого тела FТв и самой жидкости FЖ
.
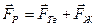Рис. 16 В случае смачивающей жидкости сила FР направлена наружу по отношению к жидкости.
При чём равновесным будет состояние системы, при котором касательная к поверхности жидкости перпендикулярна вектору результирующей силы FР. Поскольку в этом случае сила FР не способна совершать работу по перемещению молекул вдоль поверхности жидкости, т.е. дальше искривлять форму поверхности жидкости. При смачивании, поверхность жидкости становиться вогнутой (рис.16 а), в случае несмачивания – выпуклой (рис.16б).
Степень искривления поверхности характеризуется краевым углом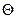 
.
Краевым называется угол между касательными к поверхностям жидкости и твёрдого тела.
Краевой угол смачивающей жидкости – острый (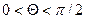
), при этом, если 
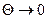, смачивание называют полным. В случае не смачивания, краевой угол изменяется в пределах 
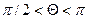, а, при 
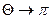, не смачивание является полным.
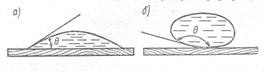Различие форм смачивающей и не смачивающей жидкостей становится хорошо заметно при небольших объёмах, например, в случае капли (рис.16).
Причём одна и та же жидкость в одном случае может быть смачивающей, как, например вода и стекло или ртуть и железо (рис. 16а); а в другом – не смачивающей – вода и парафин, или ртуть и стекло (рис. 16б).
Рис. 16
В обычных сосудах смачивание или не смачивание можно наблюдать лишь у стенок сосуда, в котором находится жидкость (рис.17).
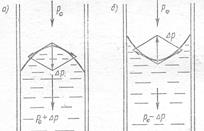
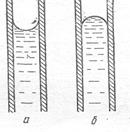
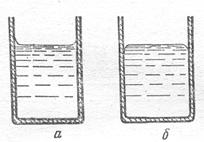
Рис. 17 Рис. 18 Рис. 19
Уменьшая размер сосуда, можно добиться того, что поверхность жидкости будет искривлена полностью (рис.18).
Полностью искривлённая поверхность жидкости называется мениском.
Сосуды, в которых поверхность жидкости является мениском, называются капиллярами.
В мениске действуют силы поверхностного натяжения, стремящиеся уменьшить его площадь. Это приводит к возникновению дополнительного давления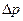 
под искривлённой поверхностью жидкости, направленного внутрь искривления этой поверхности (рис.19).
Таким образом, давление под поверхностью смачивающей жидкости уменьшится на величину 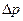(рис.19б), а не смачивающей – увеличится (рис.19 а).
Величина дополнительного давления 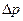определяется по формуле Лапласа:
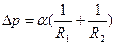, (23)
где R1 и R2 – радиусы двух взаимно перпендикулярных сечений поверхности жидкости в данной точке (рис.20).В случае сферической поверхности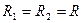 
, поэтому Лапласово давление будет равно:
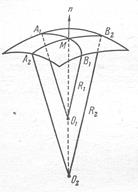
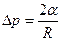. (24)
Изменение давления под искривлённой поверхностью жидкости обуславливает так называемые капиллярные явления.
Под капиллярными явлениями понимают поднятие или опускание жидкости в капиллярах, вызванные её поверхностным натяжением.
Рассмотрим смачивающую жидкость, поднявшуюся по капилляру на некоторую высоту h (рис.21). В момент погружения капилляра в жидкость её уровень как внутри, так и снаружи капилляра был одинаковым. Однако,
вследствие искривления поверхности, давление жидкости внутри капилляра станет меньше на величину давления Лапласа
,
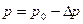Рис. 20 где р 0 – атмосферное давление.
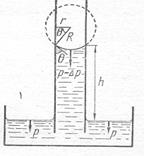Чтобы компенсировать возникший недостаток давления, жидкость поступает внутрь капилляра, и остановится лишь тогда, когда её гидростатическое давление не станет равным давлению Лапласа т.е.
.
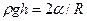Из полученной формулы выразим высоту поднятия жидкости по капилляру h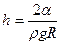 
,
где R - радиус кривизны поверхности.
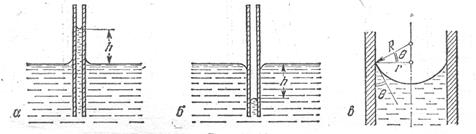
На практике удобнее использовать не радиус искривления поверхности, а радиус капилляра r, равный, согласно рисунку 21
Рис. 21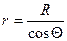 
.
Таким образом, получаем: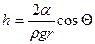 
- формула Жюрена. (25)
Из формулы Жюрена следует два вывода:
1. При смачивании жидкость будет подниматься (h > 0), а при несмачивании – опускаться (h < 0) по капилляру (рис.22).
2. Чем уже капилляр, тем выше в нём уровень жидкости.
Поверхностное натяжение и, обусловленные им капиллярные явления имеют достаточно широкое распространение.
Это почвенная капиллярность, обуславливающая подъём влаги по профилю почвы; подъём влаги по межтканевым полостям стеблей растений; питание некоторых насекомых с
Рис. 22 помощью органов, представляющих собой капилляры – хоботков и др.
Капиллярность используется в технологических процессах в ряде отраслей производства.
В клиниках определяют КПН физиологических жидкостей в диагностике заболеваний; в судостроении используются материалы, в наименьшей степени смачиваемые водой и, тем самым, уменьшающие трение; в устройстве автоматических дозаторов; для отбора излишков жидкостей в технологических процессах, например припоя при пайке и т.д.
