Статистические методы проверки адекватности математических моделей

Если имеются или могут быть получены необходимые и достоверные экспериментальные данные, для проверки адекватности моделей можно использовать методы математической статистики.

Математически задача проверки адекватности модели формулируется как задача проверки предположения о том, что значение отклика модели W_m отличается от реального отклика системы W не более чем на заданную величину e*:

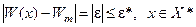. (3.3)

Однако, истинное значение отклика системы никогда неизвестно. Полученный в результате эксперимента отклик 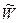в силу неконтролируемого дрейфа системы, разброса характеристик ее элементов и, наконец, просто ошибок измерения представляет собой случайную величину, отличающуюся от W. Поэтому при сравнении результатов математического и физического экспериментов 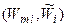будет получена совокупность случайных величин {e _i }: , среди которых могут оказаться как величины, удовлетворяющие условию (3.3), так и не удовлетворяющие ему.

Можно ли считать, что полученные отклонения (e _i > e*) объясняются случайными причинами или их наличие должно быть признано существенным, что приводит к отказу от проверяемой модели. Для решения этого вопроса на основе выборки случайных величин {e _i } строят статистические критерии, по которым оценивают адекватность модели.

 

Гипотеза об адекватности модели действительности (гипотеза Н₀) может быть сформулирована как предположение о том, что полученная совокупность {e_i} не дает оснований отказаться от рассматриваемой модели. Иными словами, модель удовлетворяет заданной точности e*.

Альтернативная гипотеза Н ₁ состоит в том, что модель не отвечает заданным требованиям (3.3) и, следовательно, должна быть отвергнута.

Так как выборка {e _i } случайна, решение о выборе одной из гипотез Н ₀ или Н ₁ носит вероятностный характер. При этом может быть допущена ошибка первого рода, состоящая в отказе от правильной модели (принимается Н ₁, когда верна Н ₀), или ошибка второго рода, состоящая в принятии ошибочной модели (принимается Н ₀, когда верна Н ₁). Вероятность ошибки первого рода обозначают через a, второго рода – b. Принято называть a риском разработчика, b – риском потребителя. Разумеется, желательно минимизировать как a, так и b. Однако, при заданном объеме экспериментальной выборки уменьшение a влечет за собой увеличение b.

На практике a задается на определенном уровне (a = 0,05; 0,01; 0,005; 0,001), при этом в 100a% случаев правильная модель отвергается.

Величина 1– b характеризует вероятность отказа от ошибочной модели, называется мощностью критерия и является мерой его эффективности.

Выбор вероятностей ошибок a и b при проверке конкретной модели зависит от ответственности решений, принимаемых на основе моделирования.

Например, если модель предназначена для управления двигателем летательного аппарата, необходимо в первую очередь минимизировать b, так как в данном случае принятие неверной модели, а значит, возможность ошибочных решений при управлении представляет больший вред, чем отказ от правильной модели.

Для оценки гипотезы об адекватности модели существует несколько критериев:

1) Критерий согласия c² Пирсона.

2) Критерий Смирнова-Колмогорова.

3) Критерий Фишера и др.

При использовании критерия c² проверке подлежит гипотеза о том, что рассматриваемая модель адекватна исследуемой системе с вероятностью р (например, р = 0,95). Это значит, что при n независимых испытаниях np значений e _i должно удовлетворять условию (3.3) и лишь в (1– р) п случаях это условие может быть нарушено.

В результате случайного эксперимента для этих событий будут получены частоты n₁ и n₂: n₁» рп; n₂ » (1– р) п; (n₁ + n₂ = п).

Частоты n₁ и n₂ отличаются от точных вероятностных оценок или из-за несоответствия модели действительности (заданная вероятность р не соблюдается), или из-за случайных отклонений.

Для оценки предположения о том, что отклонения n₁ и n₂ от соответствующих вероятностей случайны, строится функция

,

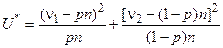представляющая собой сумму квадратов отклонений, нормированных на соответствующие вероятности.

Полученное значение U ^* сравнивается с табличным значением при заданном уровне риска a. Если U ^* превышает пороговое значение 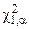, модель должна быть отвергнута, и принимается гипотеза Н ₁. Если U 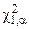^*£ , экспериментальные данные не противоречат гипотезе об адекватности модели, и принимается гипотеза Н ₀.

Необходимым условием использования критерия c² является многочисленность экспериментальных данных (не меньше 20).

Критерий Смирнова-Колмогорова основан на максимальном значении отклонений

.

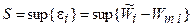Для заданной экспериментальной выборки строится вспомогательная функция

,

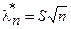которая сравнивается с пороговым значением l _{n ,a}, определенным по таблицам распределения функции Смирнова-Колмогорова.

При 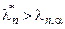модель должна быть отвергнута, а при 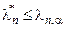экспериментальные данные не противоречат гипотезе об адекватности модели.

Критерий Смирнова-Колмогорова целесообразно использовать при относительно малых выборках, когда критерий c² оказывается неэффективным.

Критерий Фишера осуществляется путем анализа дисперсий. Если дисперсия, характеризующая ошибку эксперимента s²(W), известна, вычисляется выборочная дисперсия S ²(e) и составляется F -отношение:

.

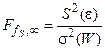Полученную величину F -отношения сравнивают с пороговым значением критерия Фишера F_{f s ,¥, a} при заданном уровне риска a.

При F_{f s ,¥} £ F_{f s ,¥, a} полученная величина S ²(e) может быть объяснена случайным разбросом экспериментальных данных и, следовательно, нет оснований для отказа от проверяемой модели.

Если F_{f s ,¥} > F_{f s ,¥, a}, полученное расхождение результатов моделирования и экспериментальных данных знáчимо и, следовательно, модель должна быть отвергнута как недостаточно точная.

 

Критерии оптимальности планов экспериментов

Одна из основных задач теории планирования эксперимента состоит в выборе такого плана эксперимента, чтобы он обеспечивал получение наилучших, в определенном смысле, результатов исследований. При этом оптимальность плана определяется задачей, стоящей перед экспериментом, видом модели, стоимостью отдельных опытов, областью планирования эксперимента и т.д..

Важнейшей характеристикой плана, влияющей как на стоимость и: длительность исследований, так и на точность получаемых результатов, является число наблюдений. По числу экспериментов планы бывают насыщенные, ненасыщенные и сверхнасыщенные. План называется насыщенным, если число экспериментов равно числу определяемых пара-t метров модели (N=к+1 для линейной модели). Однако такой план не позволяет определить адекватность модели. Если N больше числа оп­ределяемых параметров, то план ненасыщенный. В некоторых задачах (например, при выявление значимых факторов из общей совокупчости [1]) используются сверхнасыщенные планы, в которых число экспериментов N меньше числа параметров модели (выявляется только часть значимых параметров).

Среди критериев оптимальности, используемых в планировании эксперимента, можно выделить две группы.

К первой группе относятся критерии, связанные с точностью оценок коэффициентов регрессии, ко второй - с ошибкой в оценке за­висимой переменной у.

К критериям первой группы относятся:

- критерий D-оптимальности. Он обеспечивает минимальный объем эллипсоида рассеяния оценок уравнения регрессии, что требует тако­го расположения точек плана в области 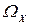, при котором определитель дисперсионной матрицы 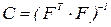был бы минимальным (или, что то же самое, );

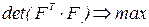- критерий А-оптимальности. Ему отвечают планы с минимальной средней дисперсией оценок коэффициентов (минимум суммы квадратов главных полуосей эллипсоида рассеивания), чему соответствует наи­меньшее значение следа дисперсионной матрицы (суммы элементов, стоящих на главной диагонали,

К критериям второй группы, связанным с ошибкой оценки поверх­ности отклика, можно отнести:

- критерий G-оптимальности. Ему отвечает план, обеспечивающий наименьшую по сравнению с другими планами величину максимальной дисперсии отклика во всей области планирования 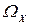. Достижение воз­можно большей точности модели связано, как правило, с лучшим ис­пользованием области планирования при проведении эксперимента;

- критерий ротатабельности (ротатабельность - инвариантность ковариационной матрицы относительно ортогонального вращения (рота­ции) системы координат). Ротатабельность плана позволяет получить одинаковую дисперсию предсказанных значений функции отклика во всех точках, равноудаленных от центра плана, вне зависимости от направления.

Кроме рассмотренных используются и другие критерии [1,2].

Следует отметить, что свойства плана связаны с видом анализи­руемой модели. При изменении вида модели свойства одного и того же плана могут меняться (см. пример).

На практике частo истинный вид модели априорно неизвестен. Поэтому первоначально эксперимент планируется исходя из предполо­жения о линейности модели относительно независимых переменных. После проведения опытов и построения такой модели проверяется ее адекватность. Если модель неадекватна, то переходят к построению модели более высокого порядка. При этом при построении плана для модели более высокого порядка целесообразно использовать точки, в которых уже проводился эксперимент.

Планы, которые обеспечивают возможность использования точек, применяемых для построения полинома степени d. в качестве подмножества точек, необходимых для оптимального плана формирования по­линома степени (d+1), называются композиционными планами порядка (d+1). Так, планы для квадратичных моделей, построенные путем до­бавления точек к плану для линейной модели, называются композици­онными планами 2-го порядка. Такое построение планов, использующих результаты предыдущих наблюдений, сокращает общее число опытов и отвечает последовательной стратегии планирования эксперимента.

Выбор критерия оптимальности плана осуществляется исходя из конкретного содержания решаемой задачи. Часто полезно бывает стре­миться к тому, чтобы один и тот же план удовлетворял нескольким критериям (например, для линейной модели вида Y=B X ортогональный план является одновременно и ротатабельным).