Предложен алгоритм размещения компонентов на печатных платах, основанный на минимизации количества цепей в горизонтальных и вертикальных сечениях платы. Такой подход позволяет учесть ещё до трассировки «перегруженные» участки печатной платы. Рис. 1, Ист. 2.
При задании схемы с помощью гиперграфа множеству вершин гиперграфа ставятся во взаимооднозначное соответствие компоненты схемы, а связи между компонентами (цепи) отображаются множеством рёбер. Печатная плата в этом случае представляется в виде рядной конструкции. Совокупность компонентов, размещённых в одном горизонтальном или вертикальном ряду платы, будем называть подсхемой. В качестве критерия оптимальности в предлагаемых алгоритмах размещения принята минимизация количества цепей между подсхемами в заданной области, т.е. реализован механизм сечений [1, 2]. Применение такого критерия позволяет равномерно заполнять монтажное пространства цепями, учесть ограничения на геометрические параметры печатного монтажа, выделить ещё до трассировки “перегруженные» участки печатных плат. Всё это значительно облегчает последующую трассировку соединений на плате.
Для реализации выбранного критерия размещения монтажное пространство печатной платы «разбивается» множеством вертикальных и горизонтальных сечений. Число цепей, пересекающих сечение, будем называть загруженностью сечения. Предлагается производить оптимизацию для тех сечений, загруженность которых больше допустимой.
Задача оптимального размещения компонентов для выбранной модели печатной платы сводится к разрезанию гиперграфа с минимизацией суммарного числа рёбер, попадающих в разрез. Для этой цели используется метод последовательного разбиения множества вершин гиперграфа на два подмножества.
При разбиении множества вершин гиперграфа Х на два подмножества Х1 и Х2 = Х/Х1 минимизируется целевая функция
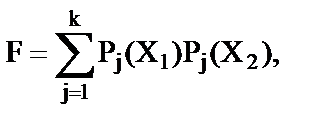 (1)
(1)
где 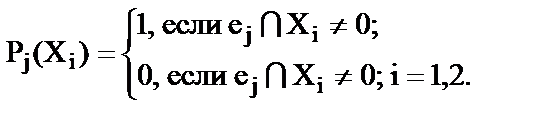
Нетрудно видеть, что произведение 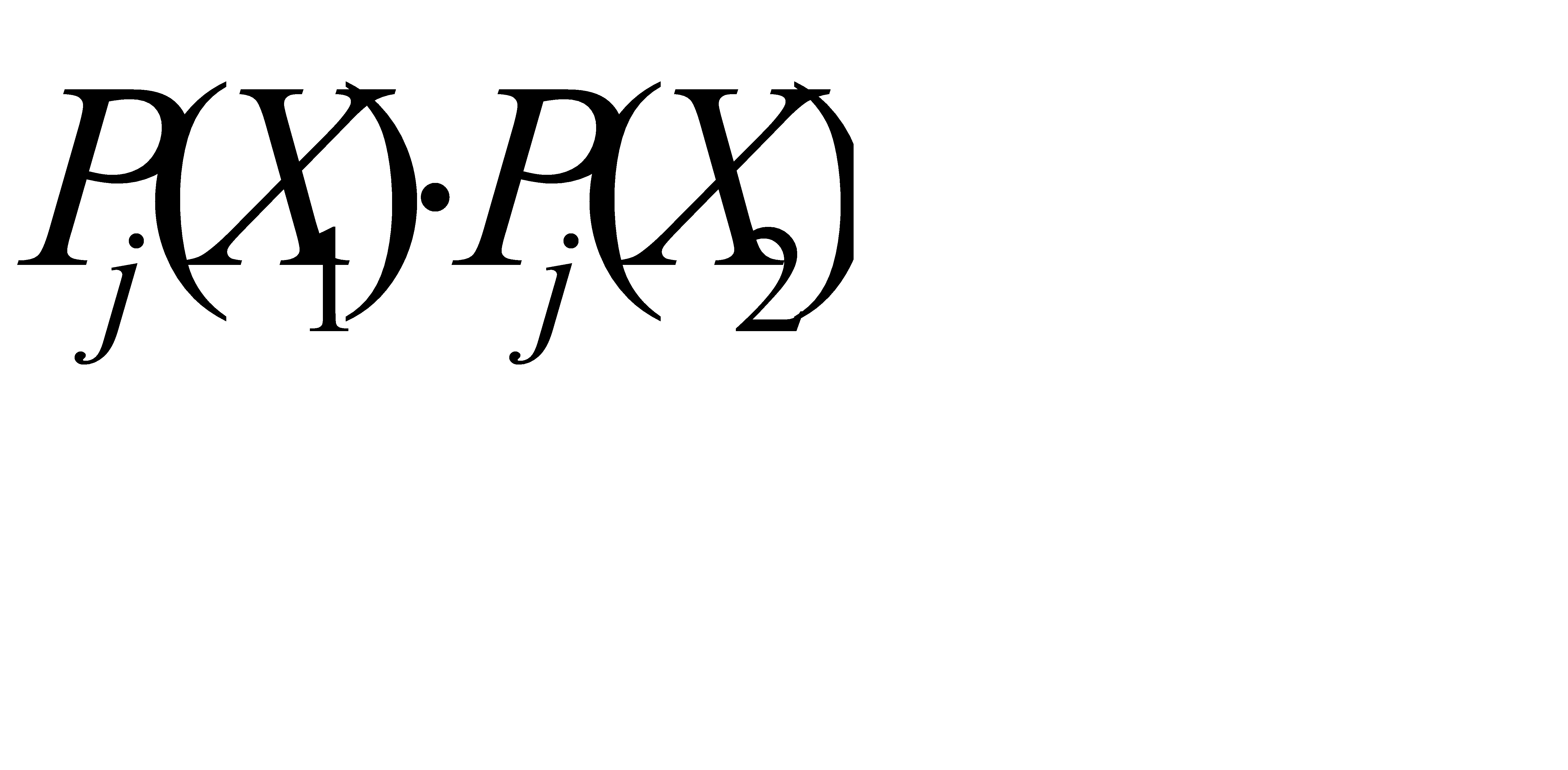 равно единице лишь в том случае, когда ребро ej попадает в разрез. Иначе говоря, это число внешних узлов выделяемой подсхемы.
равно единице лишь в том случае, когда ребро ej попадает в разрез. Иначе говоря, это число внешних узлов выделяемой подсхемы.
Разрезание гиперграфа выполняется с помощью двух алгоритмов. Сначала находится первоначальное разбиение множества Х на Х1 и Х/Х1, которое затем уточняется с помощью итерационного алгоритма.
Суть первого алгоритма состоит в последовательном переборе вершин из Х, пригодных для включения в подмножество Х1. Для выбора таких вершин  введём оценку at следующего вида:
введём оценку at следующего вида:
 (2)
(2)
где 
rtj – элемент матрицы инциденций гиперграфа,
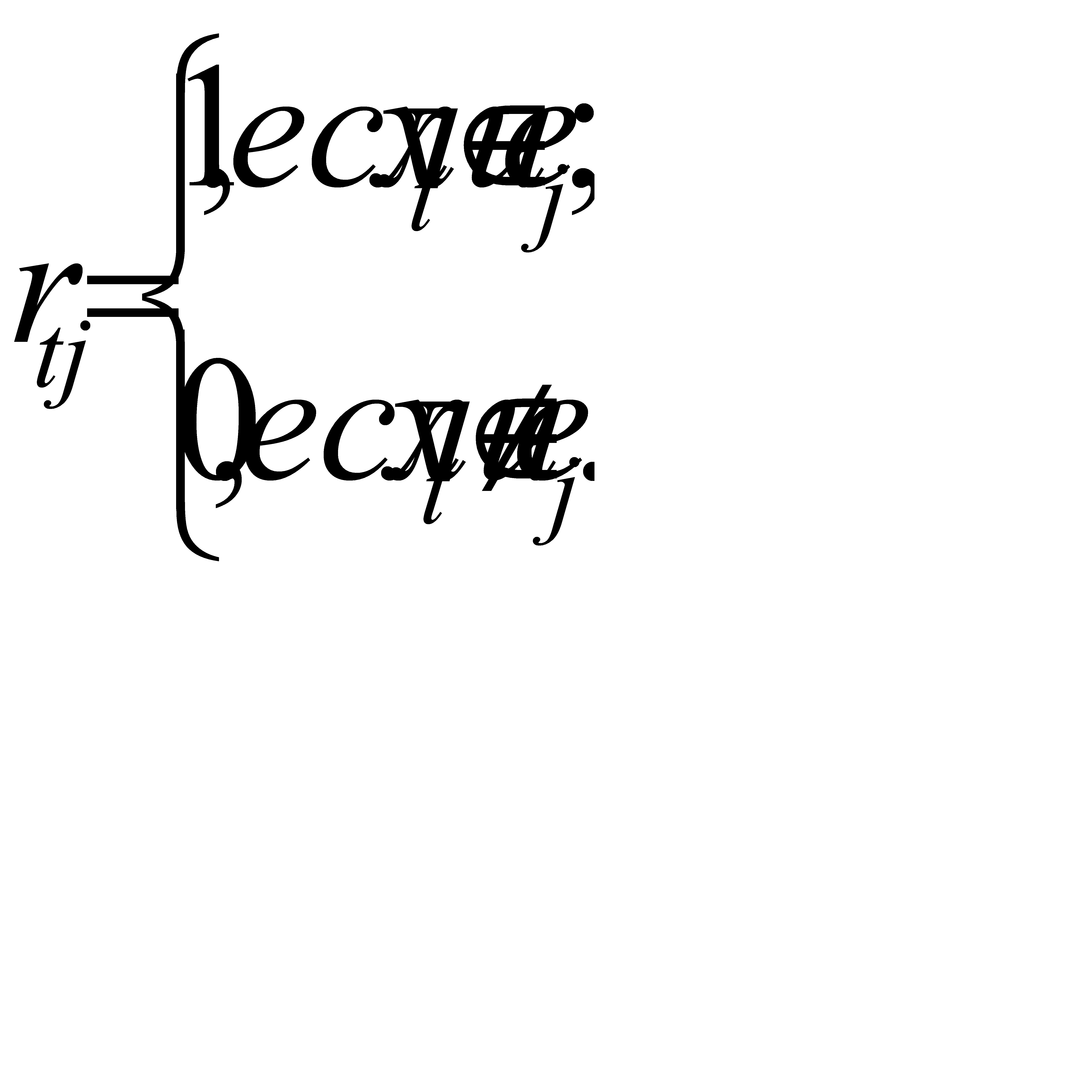
Из (2) видно, что оценка at отражает увеличение числа разрезаемых рёбер при переносе вершины xt из X/X1 в X1.
Исходя из содержательного смысла оценки (2), на каждом шаге последовательного алгоритма в множество Х1 включаем вершину, для которой величина оценки наименьшая. Формирование множества Х1 прекращается при нарушении ограничения 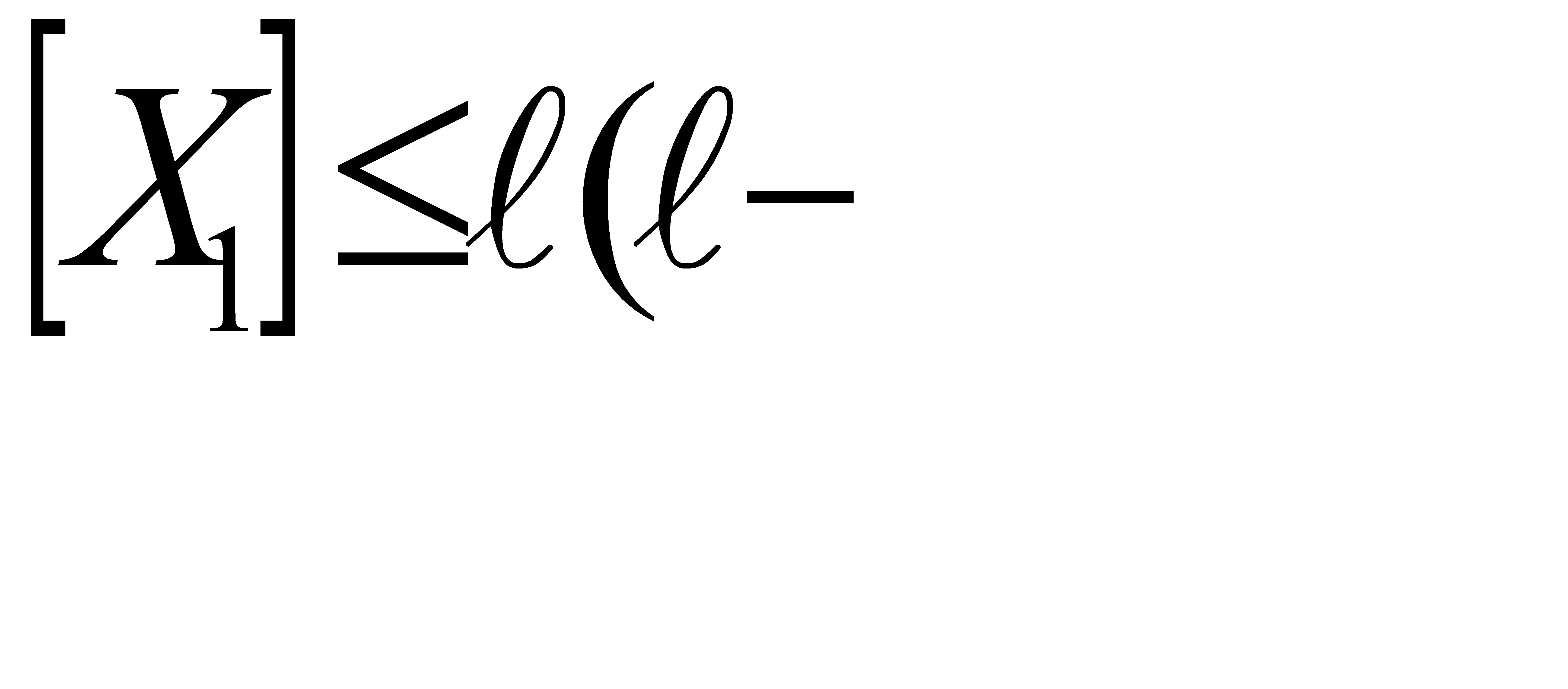 заданное число элементов подсхемы).
заданное число элементов подсхемы).
Суть второго алгоритма, итерационного, заключается во взаимной перестановке на каждом шаге таких подмножеств 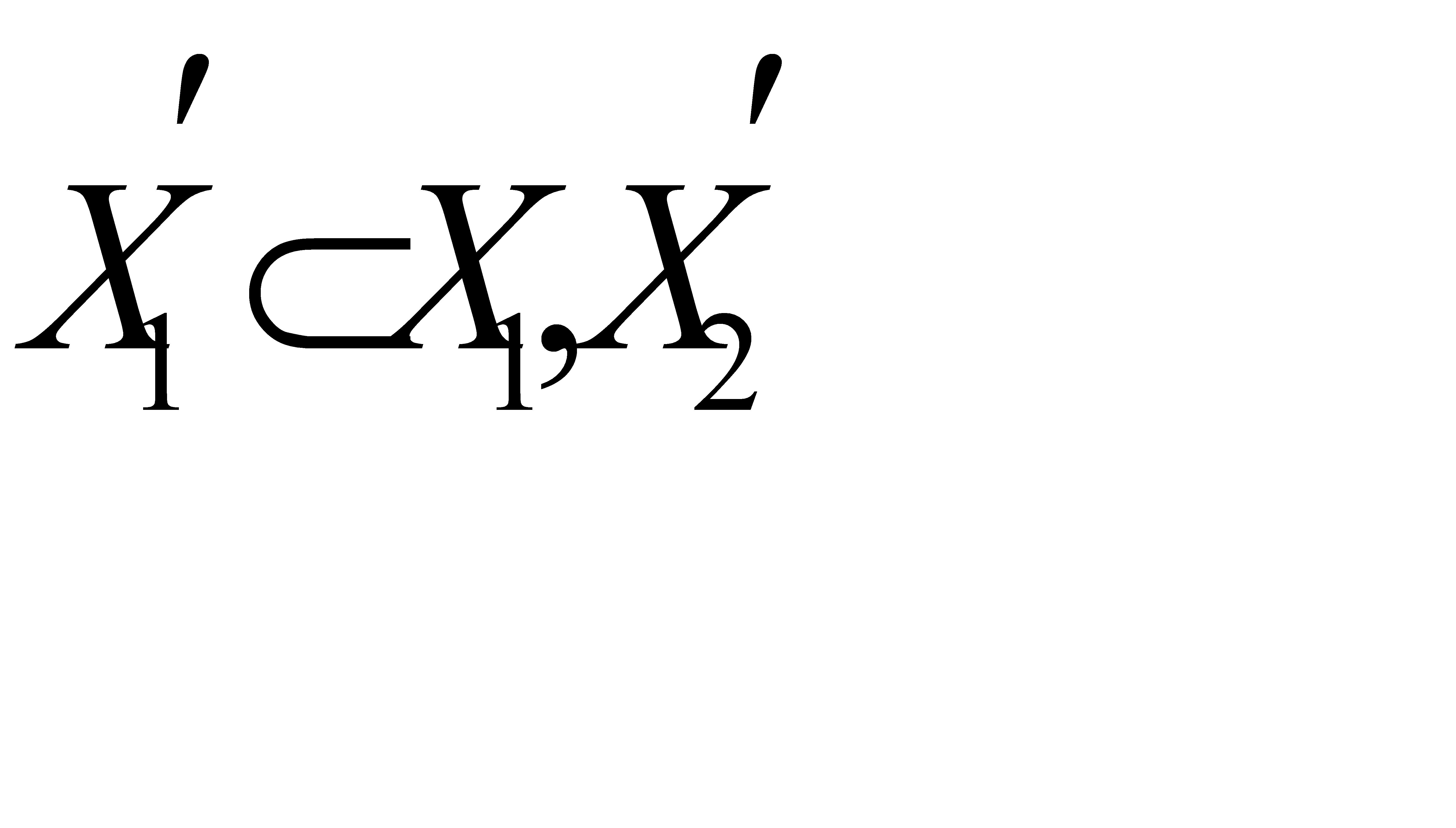 вершин гиперграфа, при которой уменьшается целевая функция (1). Для обоснования выбора
вершин гиперграфа, при которой уменьшается целевая функция (1). Для обоснования выбора  и
и  введём оценки:
введём оценки:
 (3)
(3)
 (4)
(4)
С учётом (1) видно, что оценка (3) отражает изменение числа рёбер между Х1 и Х2 при переносе вершин подмножества  из Х1 и Х2, а оценка (4) – такое изменение при переносе вершин подмножества
из Х1 и Х2, а оценка (4) – такое изменение при переносе вершин подмножества  из Х2 и Х1.
из Х2 и Х1.
Кроме того, введём оценки
 (5)
(5)
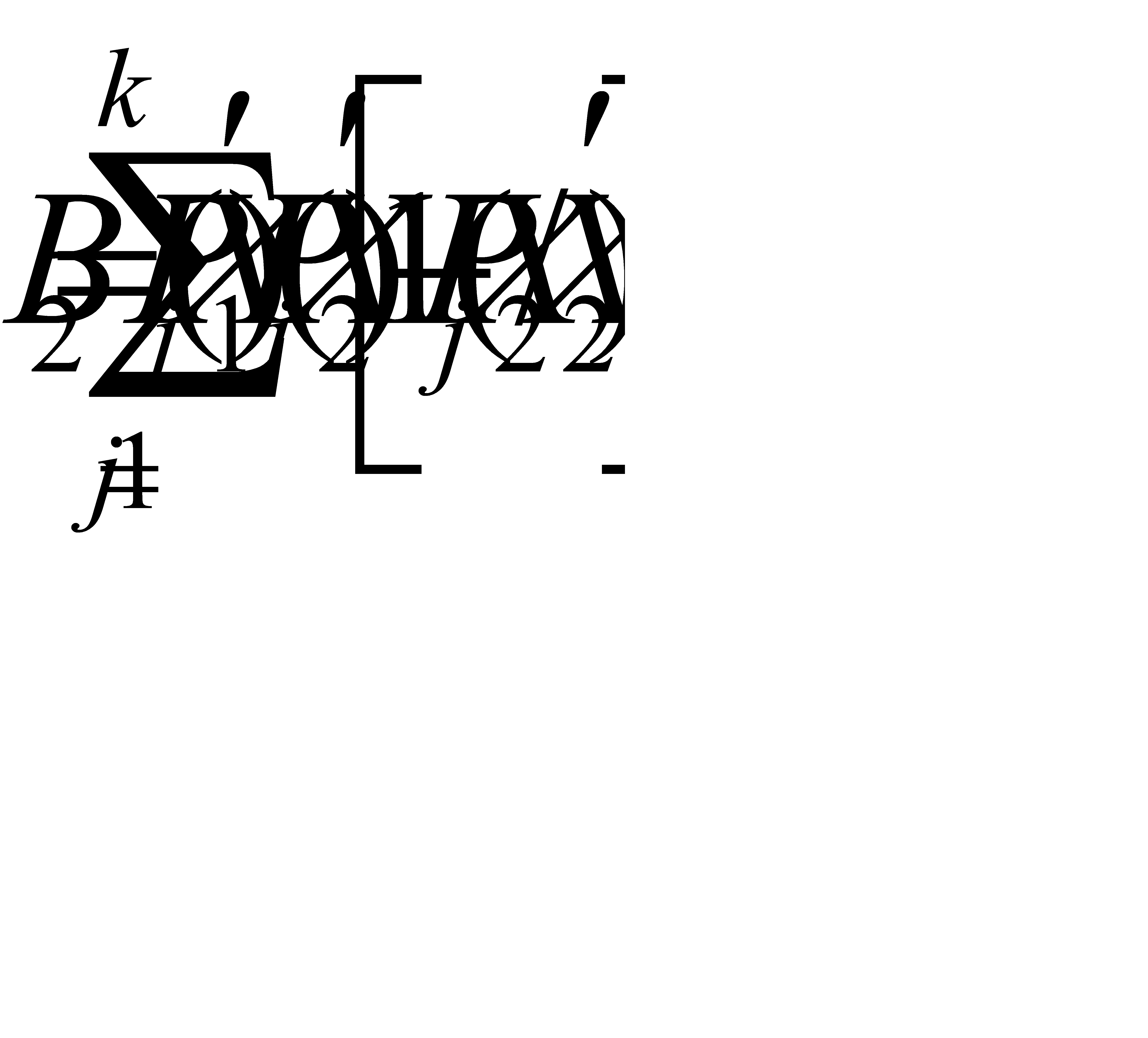 (6)
(6)
Оценки (5), (6) отражают уменьшение числа разрываемых рёбер, содержащих одновременно вершины из  и
и  , при переносе
, при переносе  в Х2 или
в Х2 или  в Х1 соответственно.
в Х1 соответственно.
Критерий выбора подмножества вершин для взаимной перестановки определяется следующим утверждением.
Взаимная перестановка подмножеств вершин  приводит к уменьшению целевой функции (1), если
приводит к уменьшению целевой функции (1), если
 (7)
(7)
Для доказательства утверждения (7) рассмотрим значения целевой функции до перестановки вершин и после неё. Обозначим значение целевой функции до перестановки через F1, а после перестановки – через F2.
Тогда запишем (рис. 1):
 (8)
(8)
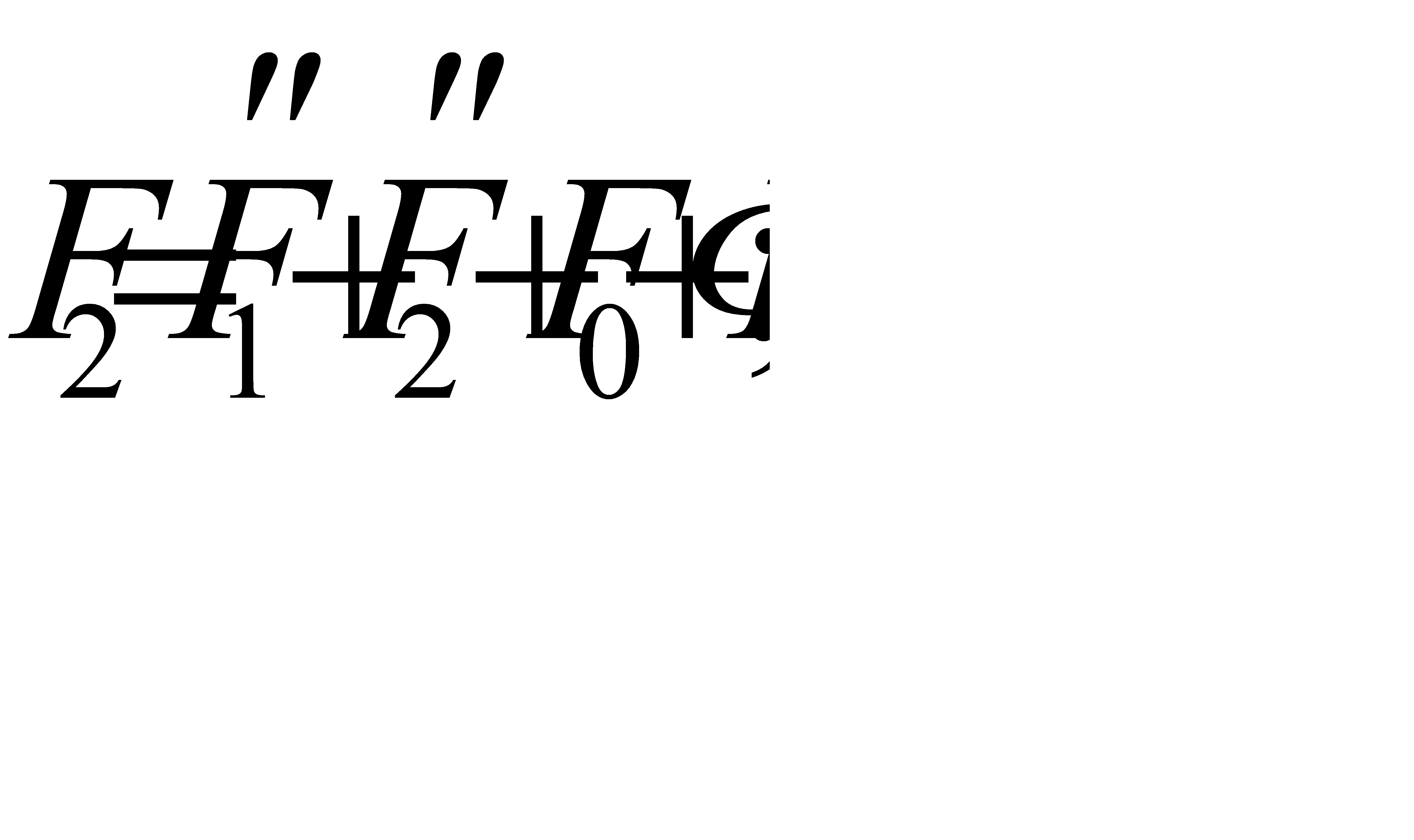 (9)
(9)
где  - число рёбер, содержащих вершины только из
- число рёбер, содержащих вершины только из  и
и 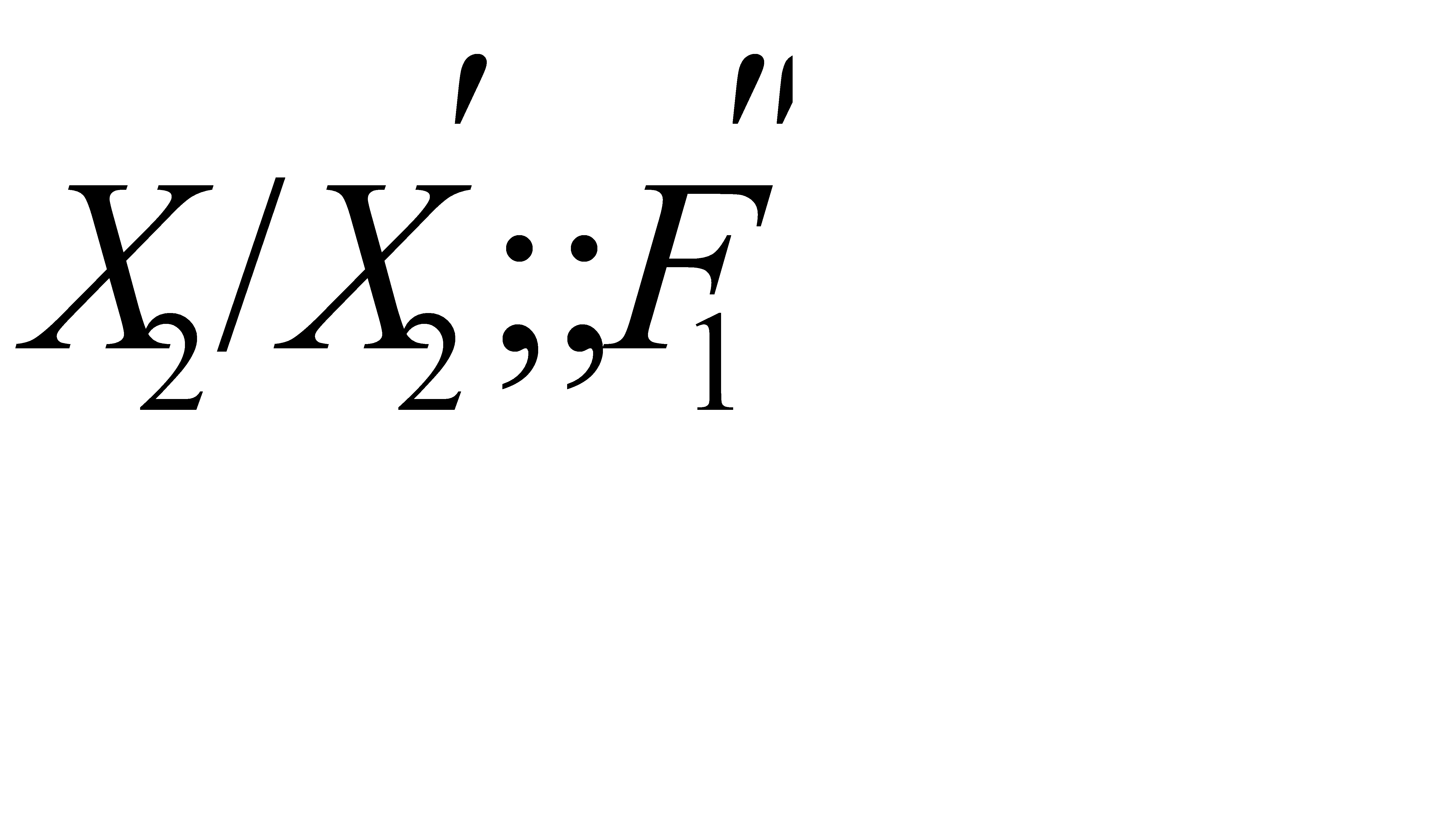 - число рёбер, содержащих вершины из
- число рёбер, содержащих вершины из  и
и 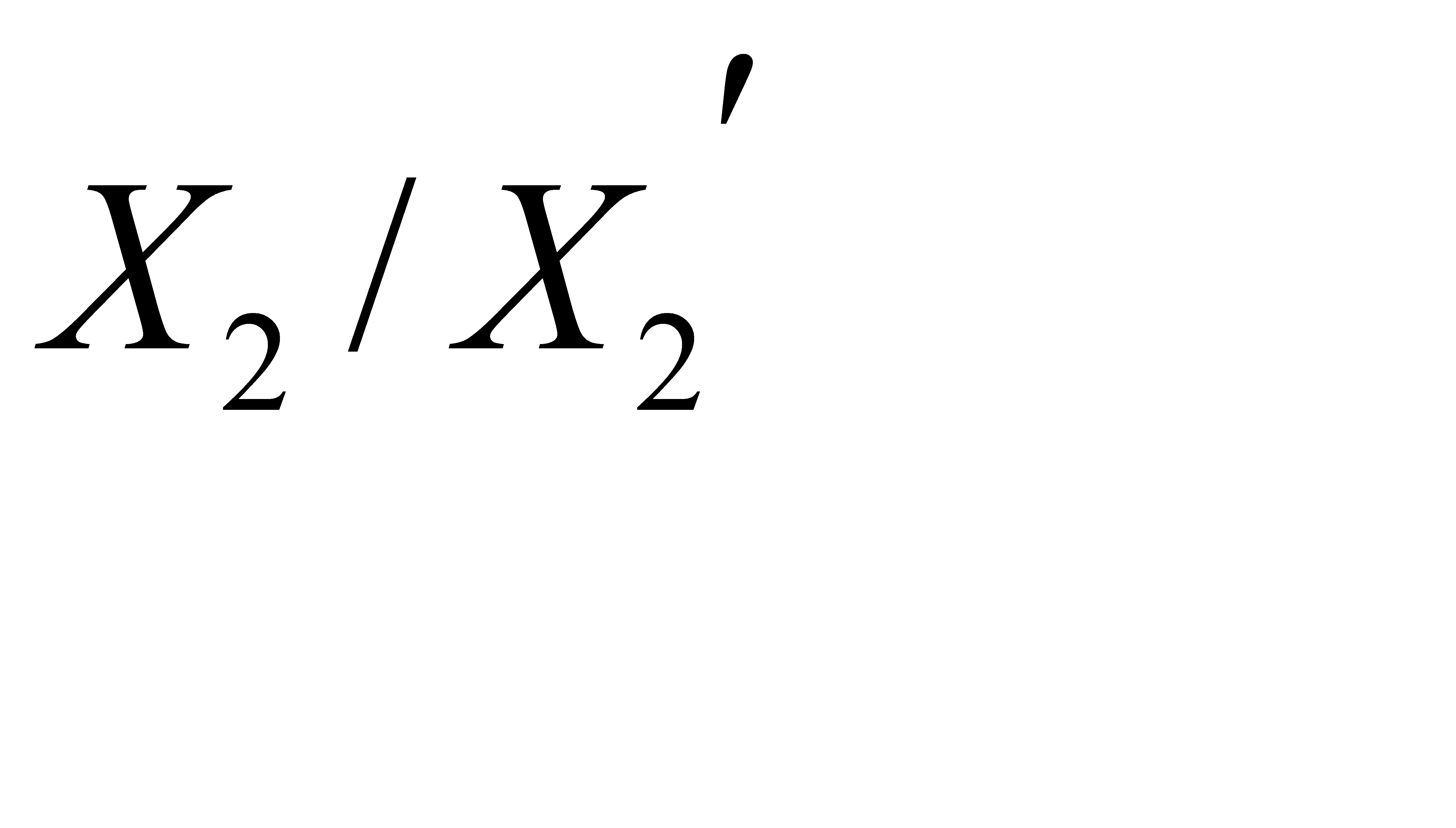 и не содержащих вершины из
и не содержащих вершины из 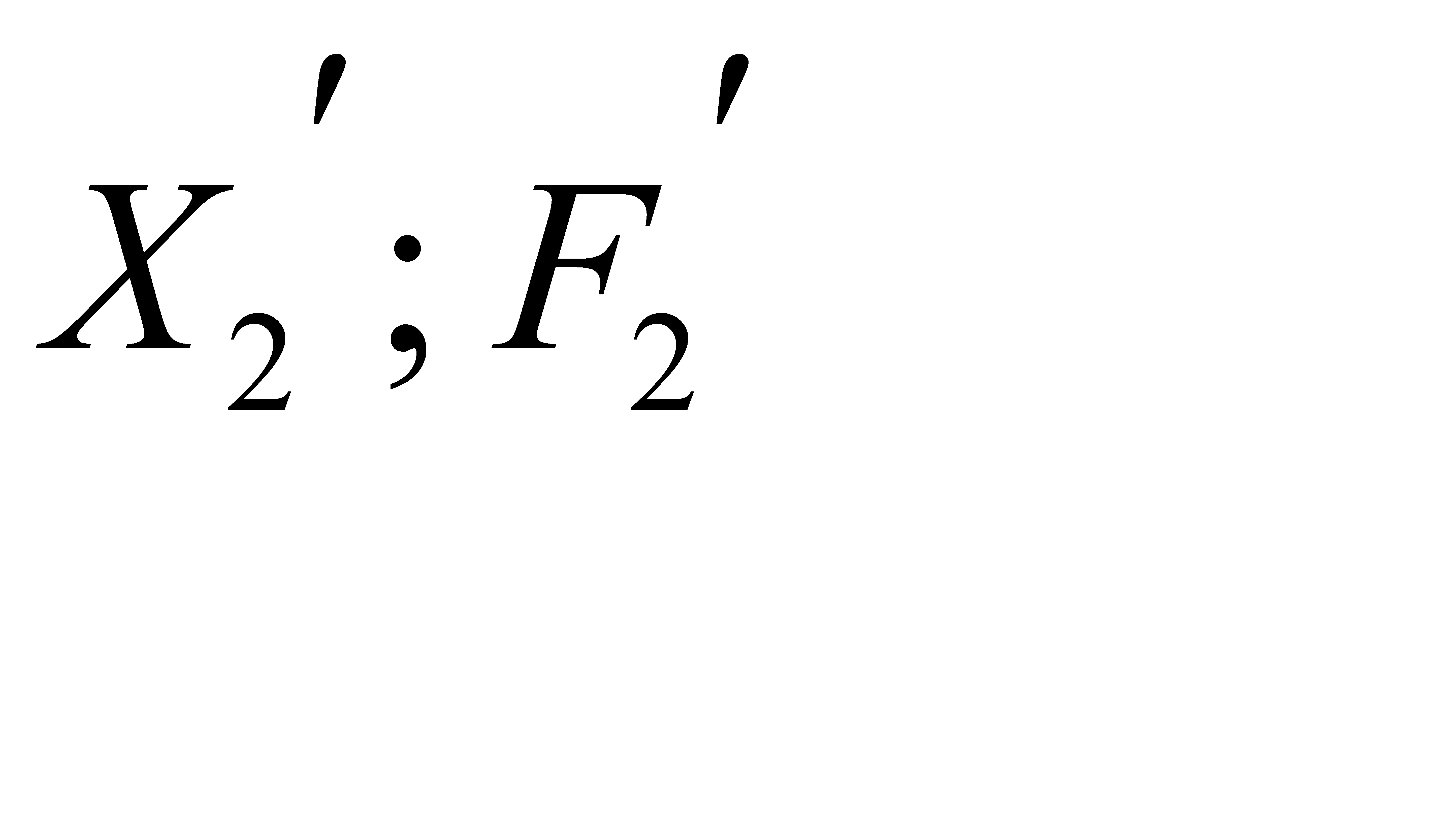 - число рёбер, содержащих вершины только из
- число рёбер, содержащих вершины только из  и
и 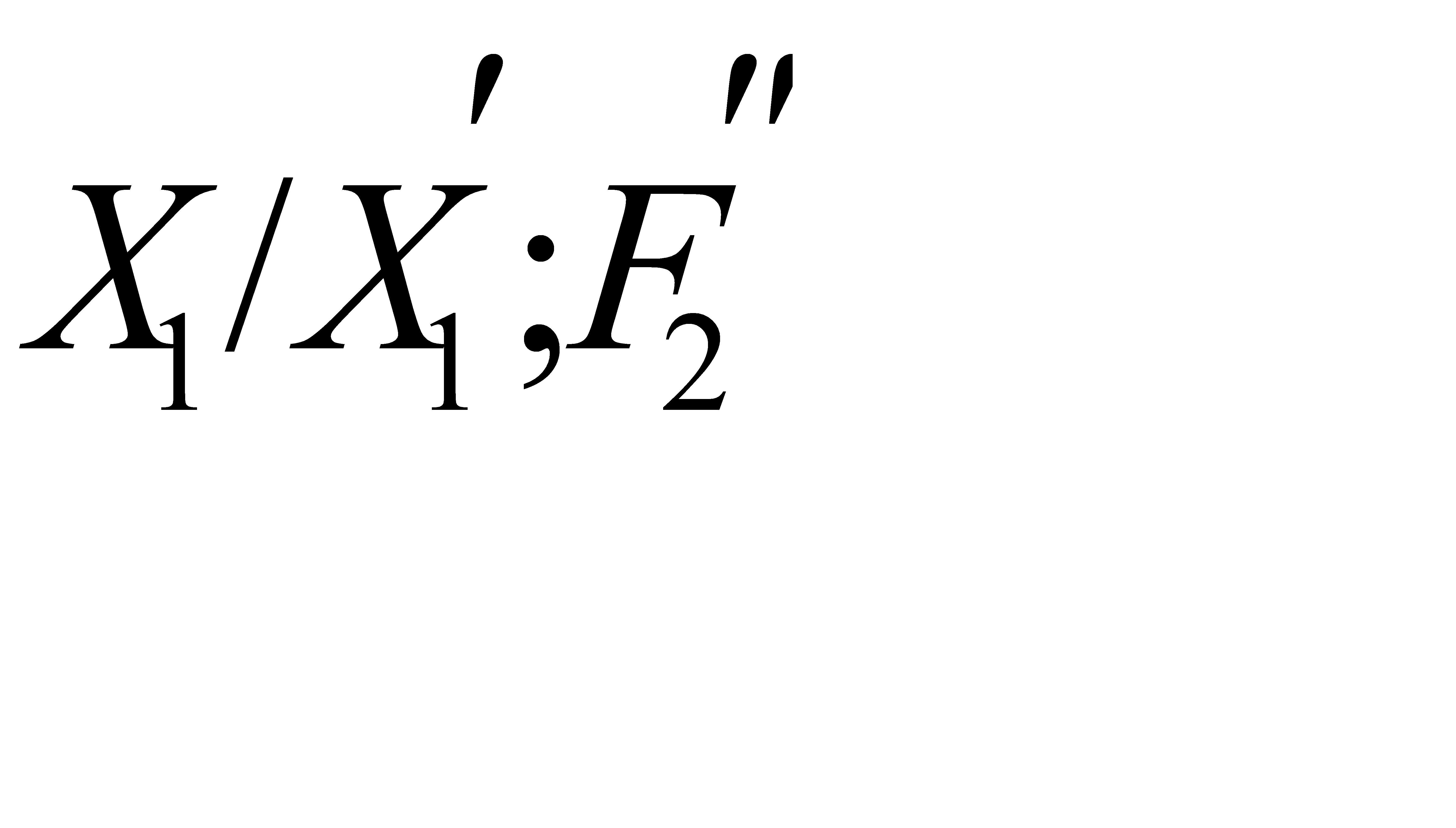 - число рёбер, содержащих вершины из
- число рёбер, содержащих вершины из  и
и  и не содержащих из
и не содержащих из  - число рёбер, связывающих Х1 и Х2 не содержащих вершин из
- число рёбер, связывающих Х1 и Х2 не содержащих вершин из  и
и  ; Ф – число рёбер, связывающих
; Ф – число рёбер, связывающих  и
и  .
.
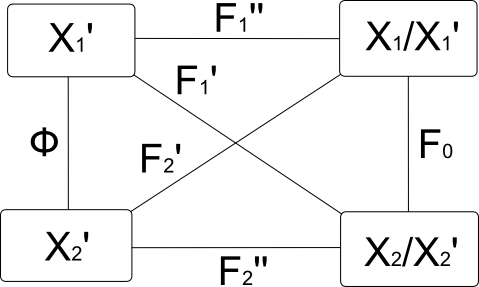
Рис. 1. Схема связи подмножеств вершин гиперграфа
Перестановка подмножеств  и
и  имеет смысл, если
имеет смысл, если
 (10)
(10)
С учётом (8), (9) имеем
 (11)
(11)
Определим согласно (1) выражения для членов, входящих в (11):
 (12)
(12)
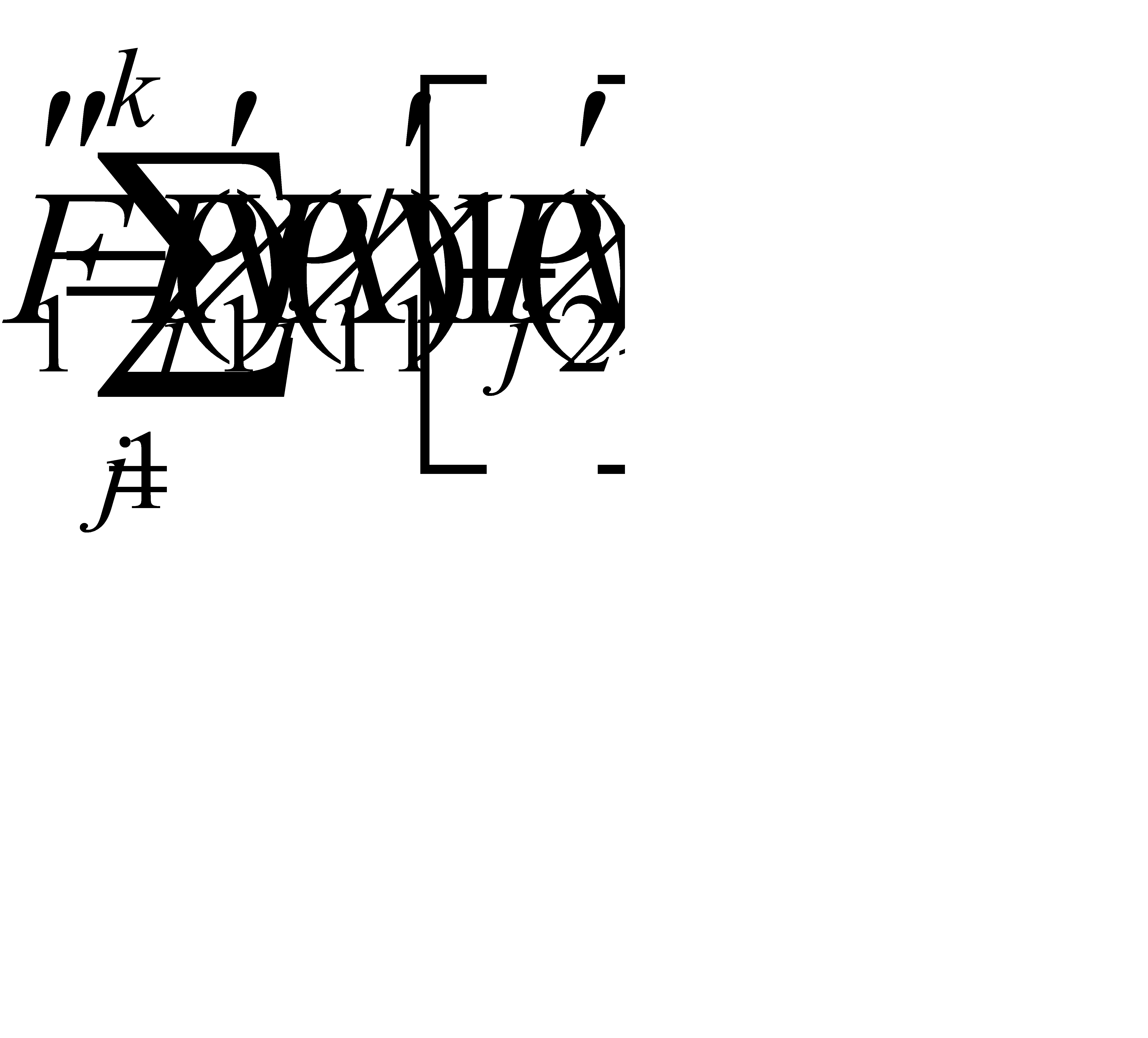 (13)
(13)
 (14)
(14)
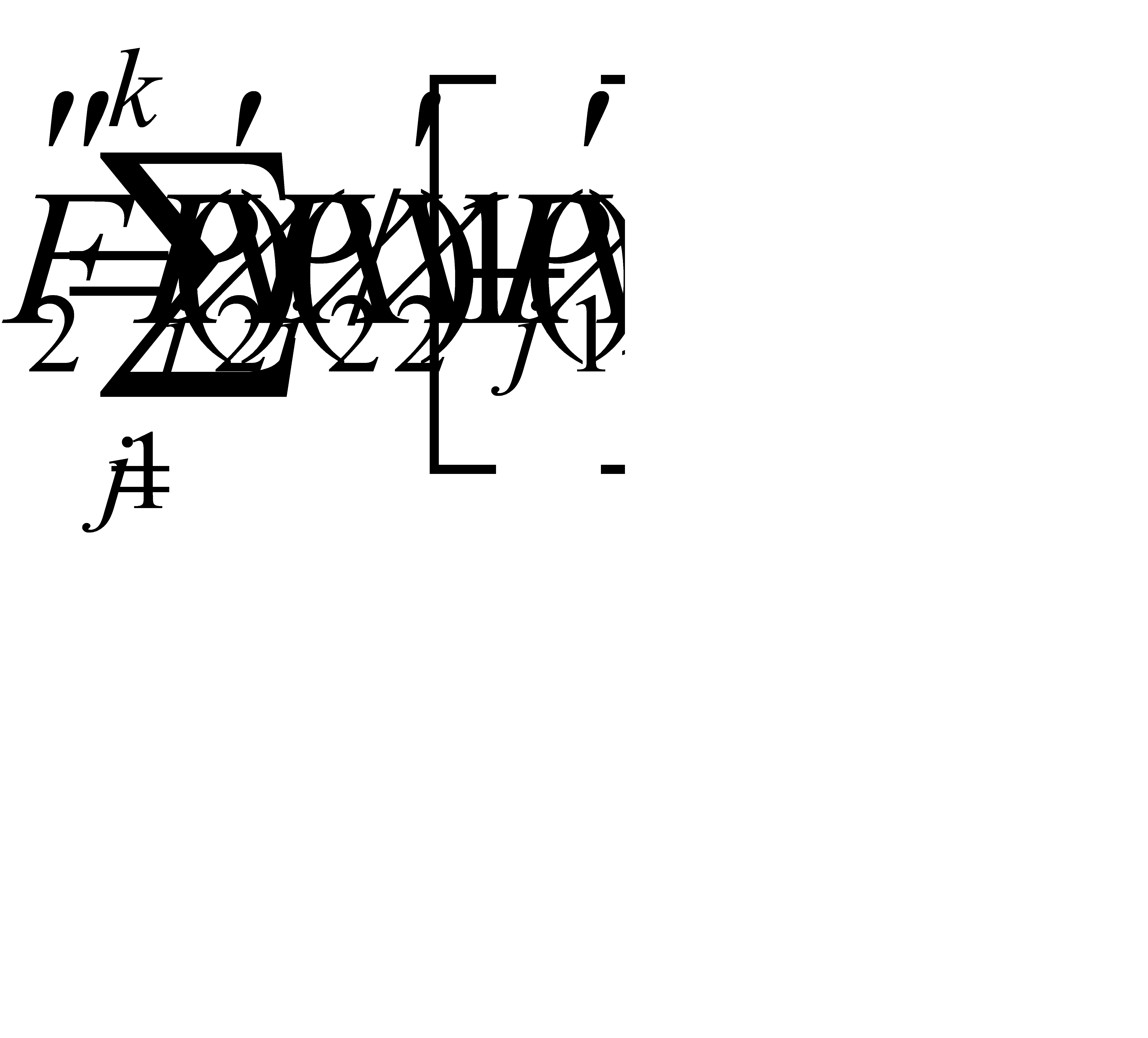 (15)
(15)
После подстановки выражений (12) – (15) в (11) и несложных преобразований получим


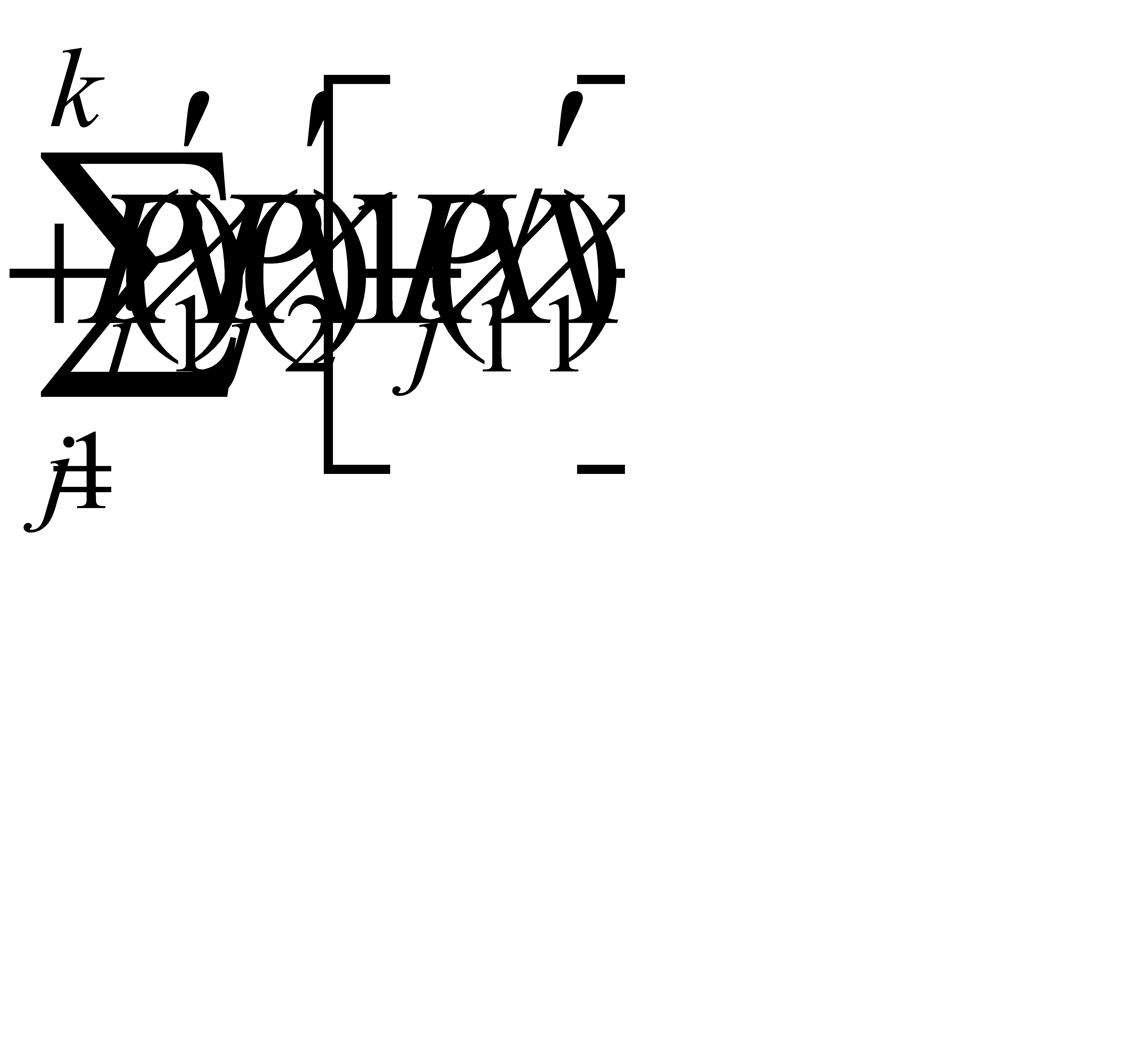

Сравнивая полученное с (10), с учётом (3) – (6) приходим к A1+A2+B1+B2<0. Утверждение (7) доказано.
Заметим, что поскольку B1 и B2 всегда положительны, то при работе алгоритма в качестве кандидатов на перестановку рассматриваются только те подмножества, для которых A1+A2<0.
Так как критерий перестановки (7) определяет величину изменения целевой функции, то на каждой итерации выбираются такие  и
и  , для которых величина G<0 наименьшая. Очевидно, что число итераций конечно, так как на каждой итерации происходит уменьшение целевой функции, которая имеет свой минимум.
, для которых величина G<0 наименьшая. Очевидно, что число итераций конечно, так как на каждой итерации происходит уменьшение целевой функции, которая имеет свой минимум.
Последовательное размещение компонентов на печатных платах производится в два этапа. На первом этапе для каждого горизонтального ряда посадочных мест формируются подсхемы путём разрезания гиперграфа схемы на m частей (m – число горизонтальных рядов). Для этого вначале формируются горизонтальные сечения платы. В ходе разрезания критерием оптимизации является минимизация числа цепей, проходящих через эти сечения. На втором этапе последовательного размещения компоненты каждой подсхемы размещаются внутри ряда путём разрезания гиперграфа каждой i-й подсхемы на ni частей (ni – количество компонентов в i-той подсхеме). Критерием размещения на этом этапе является минимизация числа цепей, проходящих через заранее сформированные вертикальные сечения платы.
На обоих этапах последовательного размещения предусмотрена возможность оперативного вмешательства в процесс размещения с целью коррекции результатов (включение компонентов в подсхемы, «фиксация» компонентов в определённом месте и т.п.).
В ходе итерационного размещения за счёт парных перестановок компонентов местами минимизируется число цепей, проходящих через горизонтальные и вертикальные сечения монтажного пространства. Для этого выбираются сечения, загруженность которых больше допустимой. Поиск парных перестановок выполняется в заданной области.
В заключение отметим, что предложенные алгоритмы применимы ко многим задачам конструкторского проектирования РЭА, распределения программ в вычислительных системах и т.п.
Список литературы:
1. Duff I. S., Reid J. K., Scott J. A. The use of profile reduction algorithms with a frontal code. Int. J. Numer. Meth. Eng, 1989. – 28. – P. 2555-2568.
2. Fialko S. Yu., Kriksunov E. Z., Karpilovskyy V. S. A sparse direct multi-frontal solver in SCAD software // Proc. Of the CMM-2003 – Computer Methods in Mechanics, June 3-6, 2003. – Gliwice, Poland. – P. 131-132.
УДК 681.14
Королёв А.Г., Ганжа С.Н., Карпенко А.В., Пояркова Л.И.






