10. Преобразование векторного пространства Ln называется нулевым, если оно каждый вектор из Ln переводит в нулевой вектор. Матрицей нулевого преобразования является нулевая матрица.
Если же каждому вектору из Ln сопоставляется этот же вектор, то преобразование называется тождественным, а его матрицей является единичная матрица.
20. Последовательное выполнение двух преобразований – преобразования 
с матрицей А и последующего преобразования 
с матрицей В является преобразованием h˚f с матрицей ВА и называется произведением преобразования f на преобразование h. В этом случае из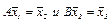 
следует ВА 
Произведение линейных преобразований ассоциативно, но не коммуникативно, т. к. в общем случае АВ ≠ ВА.
Произведение любого преобразования f на тождественное преобразование равно самому преобразованию f.
30. Суммой преобразования с матрицей А и преобразования с матрицей В является преобразование с матрицей А + В.
40. Потребуем, чтобы для каждого образа 
линейного преобразования L 
= 
существовал единственный прообраз . Это означает, что система уравнений (13) должна быть разрешима относительно х1, х2,…., хn для любых у1, у2,…., уn. Это возможно только в случае, когда det L ≠ 0, т.е. матрица L невырожденная. И тогда существует преобразование L–1 = 
, называемое обратным преобразованию L = .
50. Пусть S – матрица линейного преобразования S = в старом базисе, N – матрица того же преобразования N 
= 
в новом базисе и Т – матрица перехода от старого базиса к новому, т. е.
= Т 
, 
= Т 
. Тогда из равенств SТ 
= S = = Т 
= ТN следует, что матрицы S и N одного и того же линейного преобразования в разных базисах связаны соотношением SТ = ТN.
Задача 0.57. В базисе 
преобразование f имеет матрицу 
Найти матрицу В преобразования f в базисе 
Решение. Матрица перехода от старого базиса к новому имеет вид 
и связывает матрицы А и В соотношением А∙Т = Т∙В. И т.к. базисные векторы линейно независимы, то detТ ≠0 и существует матрица Т –1.
Т –1 = 
.
Выполним умножение матриц и найдем В = Т –1 ·А · Т.
Т -1 ·A= 
= 
B= 
Ответ: В = 
Задача 0.58. Заданы линейно независимые векторы 
= (2, 3, 5)T, 
= (0, 1, 2)T, 
= (1, 0, 0)T. Найти линейное преобразование, переводящее векторы , 
, 
соответственно в векторы
= (1, 1, 1)T, 
= (1, 1, – 1)T и 
= (2, 1, 2)T.
Решение. Полагаем, что 
- матрица искомого линейного преобразования, тогда по условию задачи должны выполняться одновременно равенства C 
, С 
, С 
или короче
СА = В, где 
матрица базиса 
и 
матрица системы векторов 
.
Т.к. det А = 1 ≠ 0, то существует 
и тогда
Ответ: С = 
§4. Собственные значения и собственные векторы линейного преобразования. Характеристический многочлен.
Пусть в n-мерном линейном пространстве ненулевой вектор коллинеарен своему образу А при линейном преобразовании с матрицей А, т. е. существует число μ такое, что А = μ . Тогда число μ называют собственным значением, а вектор - принадлежащим числу μ собственным вектором преобразования. В этом случае равенство А = μ , А = μЕ , А – μЕ = 
, (А – μЕ) = означает, что система однородных уравнений
(14)
имеет ненулевое решение = (х1, х2,…, xn). Это возможно только в случае, если det (А–μЕ)= 0, т. е. если собственное значение μ является корнем уравнения
(15)
которое называется характеристическим уравнением преобразования. Если «раскрыть» определитель, то левую часть этого уравнения называют характеристическим многочленом матрицы А. Он может иметь не более n действительных корней, сумма которых равна следу матрицы А.
Таким образом, если требуется найти собственные векторы преобразования с матрицей А n-го порядка, то составляют характеристическое уравнение (15). Его решениями являются собственные значения матрицы А и для каждого из них составляют систему (14). Решением каждой такой системы уравнений с точностью до числового множителя является собственный вектор .
Задача 0.59. Линейное преобразование задано в некотором базисе матрицей 
. Найти собственные значения и принадлежащие им собственные векторы линейного преобразования.
Решение. Составим характеристическое уравнение и найдем его действительные корни.
μ1,2 =1, μ3 = 4. Таким образом, имеются два собственных значения, причем одно из них двукратное.
Ищем собственные векторы, принадлежащие первому двукратному собственному значению μ = 1.
С этой целью решаем систему уравнений (L – μ1 E) 
или
Т.к. ранг системы равен 1, а количество неизвестных 3, то система имеет 2 линейно независимых частных решения.
Если полагать х1=1, х2 = 0, то получим х3=-1 и первый собственный вектор 
= (1; 0; -1)T
Если полагать х1=0, х2 = 1, то получим х3=0 и второй собственный вектор 
= (0; 1; 0)T.
Ищем собственный вектор, принадлежащий числу μ = 4.
Если полагать х1=1, то получим х3=2 и третий собственный вектор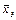 
= (1; 0; 2)T.
Ответ: 
Перечислим основные свойства собственных векторов и собственных значений.
1. Если собственные векторы принадлежат различным собственным значениям, то они линейно независимы.
Если полагать противное, т.е. считать собственные векторы линейно зависимыми и 
, то при μ1 ≠ μ2 из 
и 
следует 
и при 
это возможно только при μ1 - μ2 = 0, что противоречит условию μ1 ≠ μ2. Следовательно, собственные векторы в действительности линейно независимы.
Из свойства 1. следует, что если в n-мерном линейном пространстве преобразование имеет n различных собственных значений, то существует базис из собственных векторов этого преобразования.
2. Если μ – собственное значение кратности S, то ему принадлежат не более S линейно независимых собственных векторов.
3. Если А и В – матрицы одного и того же линейного преобразования в разных базисах, то характеристические многочлены этих матриц совпадают.
Действительно, учитывая, что В = Т -1АТ и Т -1 μЕТ = μТ -1ЕТ= μ Т -1Т = μЕ, имеем det(B-μE) =
=det(Т -1АТ – Т -1μEТ) = det [Т -1(А - μE)T] = det Т -1 ∙ det (A -μE)∙det Т = det (A - μE)· det Т -1 · det T =
=det (A-μE), т.е. det (B - μE) = det (A - μE).
Из этого свойства следует, что характеристический многочлен матрицы А можно считать характеристическим многочленом преобразования в любом базисе.
А тогда все матрицы линейного преобразования имеют один и тот же набор собственных значений.
4. Матрица линейного преобразования в некотором базисе имеет диагональный вид тогда и только тогда, когда все векторы базиса являются собственными векторами.
Задача 0.60. Линейное преобразование с матрицей А = 
имеет собственные векторы
= (1; 0; -1)T, 
= (1; 1; -1)T и 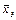= (1; 0; 2)T. Найти матрицу этого линейного преобразования в базисе 
.
Решение. Составим матрицу перехода к новому базису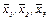 
и вычислим обратную ей матрицу.
Матрицу В линейного преобразования в новом базисе находим по формуле В = Т -1АТ.
Т -1А= 
В= 
Ответ: В базисе из собственных векторов линейное преобразование имеет диагональную матрицу
В= 
.
