Преобразование прямоугольной декартовой системы координат на плоскости.

Тема 5. Линейные преобразования.

Системой координат называют способ, позволяющий с помощью чисел однозначно установить положение точки относительно некоторой геометрической фигуры. Примерами могут служить система координат на прямой – координатная ось и прямоугольные декартовы системы координат соответственно на плоскости и в пространстве.

Выполним переход от одной системы координат xy на плоскости к другой системе , т.е. выясним, как связаны между собой декартовы координаты одной и той же точки в этих двух системах.

Рассмотрим сначала параллельный перенос прямоугольной декартовой системы координат xy, т. е. случай, когда оси и новой системы параллельны соответствующим осям x и y старой системы и имеют с ними одинаковые направления.

Если известны координаты точек M (x; y) и (a; b) в системе xy, то (рис.15) в системе точка М имеет координаты: .

Рассмотрим далее поворот системы xy на угол «против часовой стрелки» и перейдем к новой системе с тем же началом О.

Пусть отрезок ОМ длины ρ образует угол с осью и . Тогда (рис.16) с осью х отрезок ОМ образует угол и координаты точки M в системе хy равны , .

Учитывая, что в системе координаты точки М равны 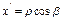и , получаем

При повороте же на угол «по часовой стрелке» соответственно получим:

Задача 0.54. Определить координаты точки М(-3; 7) в новой системе координат x^/y^/ , начало 0^/ которой находится в точке (3; -4), а оси параллельны осям старой системы координат и одинаково с ними направлены.

Решение. Подставим известные координаты точек М и О^/ в формулы: x^/ = x-a, y^/ = y-b.
Получим: x^/ = -3-3=-6, y^/ = 7-(-4)=11. Ответ: М^/ (-6; 11).

§2. Понятие линейного преобразования, его матрица.

Если каждому элементу х множества Х по некоторому правилу f соответствует один и только один элемент y множества Y, то говорят, что задано отображение f множества Х в множество Y, а множество Х называют областью определения отображения f. Если, в частности, элементу х₀ Î Х соответствует элемент у₀ Î Y, то пишут у₀ = f (х₀). В этом случае элемент у₀ называют образом элемента х₀, а элемент х₀ - прообразом элемента у₀. Подмножество Y₀ множества Y, состоящее из всех образов, называют множеством значений отображения f.

Если при отображении f различным элементам множества Х соответствуют различные элементы множества Y, то отображение f называют обратимым.

Если У₀=У, то отображение f называют отображением множества Х на множествоY.

Обратимое отображение множества Х на множество Y называют взаимно однозначным.

Частными случаями понятия отображения множества в множество являются понятие числовой функции и понятие геометрического отображения.

Если отображение f каждому элементу множества Х сопоставляет единственный элемент этого же множества Х, то такое отображение называют преобразованием множества Х.

Пусть задано множество n-мерных векторов линейного пространства L_n.

Преобразование f n-мерного линейного пространства L_n называют линейным преобразованием, если

для любых векторов из L_n и любых действительных чисел α и β. Иначе говоря, преобразование называется линейным, если линейная комбинация векторов переходит в линейную комбинацию их образов с теми же коэффициентами.

Если в некотором базисе задан вектор и преобразование f линейное, то по определению , где -образы базисных векторов.

Следовательно, линейное преобразование вполне определено, если заданы образы базисных векторов рассматриваемого линейного пространства:

(12)

Матрицу в которой k-тый столбец является координатным столбцом вектора в базисе , называют матрицей линейного преобразования f в этом базисе.

Определитель det L называют определителем преобразования f и Rg L называют рангом линейного преобразования f.

Если матрица линейного преобразования невырожденная, то и само преобразование невырожденное. Оно преобразует взаимно однозначно пространство L_n в себя самого, т.е. каждый вектор из L_n является образом его некоторого единственного вектора.

Если матрица линейного преобразования вырожденная, то и само преобразование вырожденное. Оно преобразует линейное пространство L_n в некоторую его часть.

Теорема. В результате применения линейного преобразования f с матрицей L к вектору 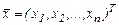получается вектор такой, что .

Доказательство. В равенство , полученное по определению, подставим разложения (12).

Получим:

Числа, записанные в скобках, являются координатами вектора по базису :

(13)

По определению операции умножения матриц систему (13) можно заменить матричным

равенством , что и требовалось доказать.

Примеры линейных преобразований.

1. Растяжение вдоль оси х в к₁ раз, а вдоль оси у в к₂ раз на плоскости ху определяется матрицей и формулы преобразования координат имеют вид: х^/ = k₁x; y^/ = k₂y.

2. Зеркальное отражение относительно оси у на плоскости ху определяется матрицей и формулы преобразования координат имеют вид: x^/ = -x, y^/ = y.

3. Поворот в реальном трехмерном пространстве на угол φ вокруг оси z определяется матрицей 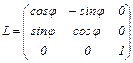и формулы преобразования координат имеют вид: x = x^/ cosφ – y^/ sin φ,
y = x^/ sinφ + y^/ cos φ, z = z^/.

Задача 0.55. Пусть А – матрица линейного преобразования в базисе ортов. Докажите, что преобразование в этом базисе, определяемое равенством , является линейным.

Доказательство. Воспользуемся определением линейного преобразования. Тогда по условию задачи в базисе ортов для любых векторов и любых действительных чисел α и β выполнены равенства:

что и требовалось доказать.

Задача 0.56. Линейное преобразование с матрицей А переводит линейно независимые векторы в векторы и соответственно. Записать матрицу А и найти образ вектора .

Решение. Образы базисных векторов определяют линейное преобразование с матрицей А = Образ вектора найдем из соотношения . Получим: 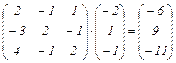. Ответ: А =