Предполагая более общую зависимост ь H от z, чем Уравнение (13),
, 
, 
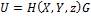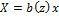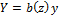(18)
и включая в Уравнение (14) константа = 1, мы получаем
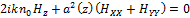(19)
Теперь мы вводим новую переменную,
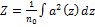(20)
которая может быть написана с помощью Уравнения (12) в форме
(21)
Как следует из Уравнения (19), множитель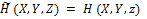 
удовлетворяет вторичному параболическому уравнению
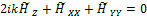(22)
Подстановкой,
(23)
где λ - произвольная комплексная константа, мы, наконец, приходим к уравнению Гельмгольца
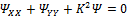(24)
Константы K и λ связаны соотношениями
, 
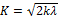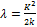
Мы можем принять любое решение Уравнения (24), для которого условие Уравнения (7) удовлетворяется. Примеры таких решений - наклоненные гауссовы пучки, которые являются теперь предметом интенсивного обсуждения (см., например, [15,16]), для которых
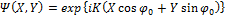(25)
где 
- произвольное комплексное число, и (см. [2,6]), те, которые соответствуют пучкам Бесселя-Гаусса, в этом случае
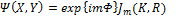(26)
где
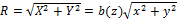(27)
, 
, 
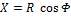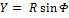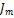является функцией Бесселя порядка mth, и Φ – вещественен и описывает обычный полярный угол. Поверхности уровня модуля таких решений для m = 0 показаны на Рис. 1 и 2.
Для функций нецелого числа m [Уравнение (26)] (а также найденные в [17]) соответствуют своего рода оптическому вихрю с дробными топологическими зарядами.
Рис. 1. Поверхность уровня модуля для решения Бесселя-Гаусса с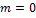 
и 
в волноводе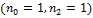 
.
Рис. 2. Поверхность уровня модуля для решения Бесселя-Гаусса с 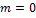и в антиволноводе .
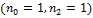У всех других решений для однородных сред, перечисленных в [4], есть свои аналоги в случае квадратичного показателя преломления.
Кроме того, мы наблюдаем, что Уравнение. (26) с 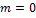обобщается сдвигами 
, 
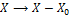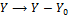, где 
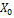и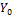 
- произвольно комплексные константы, и подстановкой
(28)
Мы называем соответствующее решение Уравнения (5) сдвинутый пучок Бесселя-Гаусса нулевого порядка. Для однородных сред и Y0 = iX0, он редуцируется к несимметричному пучку Бесселя-Гаусса нулевого порядка, описанному в [18] посредством другого подхода. Сдвинутые пучки Бесселя-Гаусса в квадратичных СМИ описаны Уравнениями (2), (23), (26), и (28), показаны на Рис. 3 и 4.
Рис. 3. Поверхность уровня модуля для сдвинутого решения Бесселя-Гаусса с m = 0, q0 =-2i, X0 = 1, и Y0 = 0 в волноводе (n> = 1, n2 = 1).
Рис. 4. Поверхность уровня модуля для сдвинутого решения Бесселя-Гаусса с m = 0, q0 = -2i, X0 = 1, и Y0 = 0 в антиволноводе (n0 = 1, n2 = -1).
ЗАКЛЮЧЕНИЕ
Вышеупомянутые результаты показывают, что теория мод Лапласа-Гаусса и Гельмгольца-Гаусса, ранее развитая для однородной среды, непосредственно обобщена к случаю среды с осесимметричным уравнением показателя преломления [Уравнение (3)], квадратичного в поперечных переменных, является ли это волноводом или антиволноводом. Наши результаты могли быть альтернативно получены, используя подход, описанный в [16], который основан на методах [19].
Вторичное параболическое уравнение [Уравнение (22)] позволяет получать интересные решения, отличные от описанных в Разделах 3 и 4. Мы планируем обсудить такие решения в другом месте.
ССЫЛКИ
