Kiselev. Лапласа-Гаусса и Гельмгольца-Гаусса параксиальные моды в средах с квадратичным показателем преломления
Aleksei P. Kiselev and Alexandr B. Plachenov. Laplace-Gauss and Helmholtz-Gauss paraxial modes in media with quadratic refraction index. Vol.33, №4 JOSA A 2016 663-666.
Рассматривается скалярная теория параксиального распространения волн в осесимметричной среде, где показатель преломления квадратично зависит от поперечных переменных. Представлены точные решения соответствующего параболического уравнения, обобщая моды Лапласа-Гаусса и Гельмгольца-Гаусса, ранее известные для однородных сред. Кроме того, дано обобщение несимметричного пучка Бесселя-Гаусса нулевого порядка
ВВЕДЕНИЕ
Параксиальные Гауссовы моды высших порядков - аппроксимационные параксиальные решения уравнения Гельмгольца,
(1)
имеющие формy
(2)
с функцией H = константа, где g - фундаментальная мода. В течение нескольких десятилетий были известны только коэффициенты H, которые являются полиномами относительно поперечных переменных. В [1] немногочленные коэффициенты H, описывающие пучки Бесселя-Гаусса в однородных средах, были первоначально введены для аксиально симметричной g. Затем общий класс решений, названных Гельмгольца-Гаусса модами, который включает моды Бесселя-Гаусса, был найден в [2] разделением переменных. В [3] этот класс был повторно получен методами теории групп. Несколько других немногочленных решений этого класса были перечислены в [4]. Вырожденный специальный класс Гельмгольца-Гаусса мод, названных модами Лапласа-Гаусса [2,5,6], описывает, в частности оптические вихри и некоторые другие спиральные решения (см., например, [7,8]).
Здесь мы представляем обобщение Лапласа-Гаусса и Гельмгольца-Гаусса параксиальных мод для аксиально симметричной неоднородной среды с квадратичным показателем преломления. Аналогично [2], подход основан на разделении переменных. Мы начинаем с уравнения Гельмгольца [Уравнение (1)] с показателем преломления n = n (x, y), квадратичным по поперечным переменным x и y [9-11]:
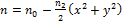(3)
Здесь, 
> 0 и 
являются вещественными константами, а k, волновое число в вакууме, может интерпретироваться, как большой формальный параметр. Положительный 
соответствует случаю волновода, отрицательный 
соответствует антиволноводу, и 
соответствует однородной среде. Для дальнейшего рассмотрения знак имеет мало значения.
Ища решения Уравнения (1) в форме
(4)
и исключая, при предположении о параксиальности, члены высших порядков (см., например, [9,11]), мы получаем аппроксимационное параболическое уравнение
(5)
где
(6)
Мы интересуемся решениями Уравнения (5), ограниченными около z-оси, то есть,
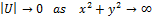(7)
ОСЕСИММЕТРИЧНЫЙ ФУНДАМЕНТАЛЬНЫЙ СПОСОБ
Осесимметричная фундаментальная мода гауссового пучка – это
где G - решение уравнения (5), имеющее форму
(8)
Здесь 
- комплексный параметр пучка 
. Функции и 
удовлетворяют уравнениям
(9)
и
(10)
Уравнения (9) и (10) подразумевают зависимость q и а от z, заданную выражениями (см. [9-11]),
(11)
и
(12)
Здесь, 
имеет отрицательную мнимую часть и функции 
, 
, 
, и 
являются записями лучевой матрицы 
(см. [9-11]). Самый известный случай для однородной среды, где 
и (см., например, [10,11])
T(z)= 
Для важного случая волноводной среды, где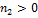 
, хорошо известный результат (см., например, [10,11]),
T(z)= 
В случае антиволноводной среды, где 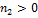, мы имеем (см., например, [10]),
T(z)= 
Последний случай, где локализация пучка быстро слабеет, когда z возрастает, представляет меньший интерес и учтен, главным образом, для полноты представления.
Обсуждение фундаментальных модовых решений для Уравнения (5) с операторами, более общими, чем Уравнение (6), может быть найдено в [12].
РЕШЕНИЯ ЛАПЛАСА ГАУССА
Мы ищем решение параболического уравнения [Уравнение (5)] в форме [2]
, 
, 
(13)
где зависимость 
будет определена позже. Подставляя Уравнение (13) в Уравнение (5) и используя уравнения
L(G)=0 мы получаем
L(U)=2ik 
Где 
. Очевидные формулы
,
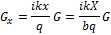
подразумевают уравнение
Мы выбираем b(z) так, чтобы
следовательно [посмотрите Уравнение (10)]
(14)
Мы, таким образом, получаем уравнение Лапласа
(15)
Мы рассматриваем H только таким образом, что произведение (2) удовлетворяет условию Уравнения (7). Общее решение Уравнения (15) – это
) (16)
где F± - произвольные аналитические функции комплексной переменной. Решения только с одним членом в правой стороне, то есть, 
или 
, соответствуют своего рода пучку спирального типа [7,8]. Функции, имеющие определенную форму
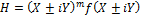(17)
где m - целое число, и f аналитична, соответствуют модам, известным как оптические вихри. Эти моды с нецелым числом m (которые появляются, например, при описании распространения пучков вдоль краев клиньев; см. [6,13,14]), разветвляются (branch) на оси Z, и не удовлетворяя n параболическому уравнению [Уравнению (5)] во всем пространстве. Такие решения, как говорят, несут дробные топологические заряды (см., например, [14]).
