3) хотя бы одно из произведений: ab, bc, ac превосходит их сумму a+b+c.
Это пример на использование логической функции «ИЛИ».
Создадим таблицу:
| a | b | c | Утверждение1 | Утверждение2 | a + b + c | Утверждение3 |
Значения a, b, c будем задавать, значения других столбцов будем рассчитывать.
4 Открыть книгу «Вычисления», лист «Логические Функции».
4 Создать таблицу, вводя названия столбцов, начиная с ячейки В14.
4 В ячейку Е15 ввести формулу для проверки Утверждения 1: «=ИЛИ(B15<0;C15<0;D15<0)».
Для проверки числа на четность используем функцию ОСТАТ (найти ее среди математических). Если остаток от деления числа на 2 равен нулю, значит число четное. Следовательно, для проверки Утверждения 2:
4 В ячейку F15 ввести формулу «=ИЛИ(ОСТАТ(B15;2)=0;ОСТАТ(C15;2)=0;ОСТАТ(D15;2)=0;)».
И для проверки утверждения 3:
4 В ячейку G15 ввести формулу «=B15+C15+D15».
4 В ячейку Н15 ввести формулу «=ИЛИ(B15*C15>G15;B15*D15>G15;C15*D15>G15)».
4 Изменяя значения a, b, c, наблюдать и анализировать изменение результата.
Пример 10.4. Имеется 2 числа: a, b. Составить логические выражения, с помощью которых можно проверить истинность утверждений:
1) хотя бы одно из них принадлежит отрезку [2,5];
2) ни одно из них не принадлежит отрезку [2,5];
Это пример на комбинированное использование логических функций.
Создадим таблицу:
| a | b | Утверждение1 | Утверждение2, вар1 | Утверждение2, вар2 |
4 Открыть книгу «Вычисления», лист «Логические Функции».
4 Создать таблицу, вводя названия столбцов начиная с ячейки В20.
Значения a, b будем задавать, значения других столбцов будем рассчитывать.
Для проверки Утверждения 1 сначала проверяется принадлежность отрезку [2,5] каждого числа в отдельности, а затем результат проверки объединяется с помощью функции «ИЛИ»:
4 В ячейку D21 ввести формулу «=ИЛИ(И(B21>=2;B21<=5);И(C21>=2;C21<=5))».
Для проверки Утверждения 2 рассмотрим 2 варианта решения.
Вариант 1. Проверим, лежит ли каждое из чисел вне отрезка [2,5], а затем результат проверки объединим с помощью функции «И»:
4 В ячейку Е21 ввести формулу «=И(ИЛИ(B21<2;B21>5);ИЛИ(C21<2;C21>5))».
Вариант 2. Если внимательно рассмотреть оба утверждения, то заметим, что Утверждение 2 противоположно Утверждению 1, поэтому для его проверки достаточно выполнить отрицание Утверждения 1:
4 В ячейку F21 ввести формулу «=НЕ(D21)».
4 Изменяя значения a, b, наблюдать и анализировать изменение результата.
Упражнения
Составить логические выражения, с помощью которых можно проверить истинность утверждений:
10.1. Сумма двух чисел превышает их произведение.
10.2. Можно построить треугольник со сторонами a, b, c.
10.3. Расстояние от точки А с координатами (xa, ya) до точки В с координатами (xb, yb) не превосходит расстояния от точки А до центра координат.
10.4. Квадрат со стороной а можно вписать в окружность радиуса R.
10.5. Точка с координатами (х, у) лежит внутри круга радиуса R с центром в начале координат.
10.6. Два числа положительные и их произведение меньше заданного значения.
10.7. Все три заданные числа нечетные.
10.8. Два заданные числа (a, b) нечетные и отрицательные.
10.9. Два числа имеют разные знаки (ноль считать положительным числом).
10.10. Три числа имеют одинаковые знаки (ноль считать положительным числом).
Работа 11. Функция ЕСЛИ
Функция ЕСЛИ используется при проверке условий. Синтаксис функции ЕСЛИ:
ЕСЛИ (ЛогичВыражение; Значение1; Значение2).
Первый аргумент (ЛогичВыражение) должен быть логического типа.
Если ЛогичВыражение имеет значение ИСТИНА, функция ЕСЛИ в качестве результата возвращает Значение1, в противном случае – Значение2.
Возвращаемый результат (Значение1 или Значение2) может быть любого допустимого в Excel типа.
Задание 11.1. В книгу «Вычисления» добавить лист с именем «ЕСЛИ». На этом листе будем выполнять примеры и упражнения этой темы.
Пример 11.1. Произвести расчет налога по правилу: 9% с суммы, не превышающей 6 млн. руб., 15% с суммы свыше 6 млн. руб.
4 В ячейки В3, С3 поместим текст-разметку: «доход», «налог».
4 В ячейку С4 поместим формулу
«=ЕСЛИ(B4<=6000000;B4*9%;6000000*9%+(B4-6000000)*15%)»
4 Изменяя величину дохода в ячейке В4, проследить за изменением величины налога.
Пример 11.2. По заданной дате определить, является ли день недели рабочим или выходным.
4 Начиная с ячейки В8, поместить названия ячеек: «дата», «день недели», «раб/вых».
4 В ячейку С9 поместить формулу «=ДЕНЬНЕД(B9;2)» (отыскать функцию ДЕНЬНЕД в категории Дата и время; второй параметр – 2 – задает порядок отсчета дней (у нас – с понедельника)).
4 В ячейку D9 поместить формулу:
«=ЕСЛИ(ИЛИ(C9=6;C9=7);"выходной";"рабочий")».
Смысл этой формулы в том, что если день недели 6 или 7, то в ячейке D9 будет помещен текст «выходной», иначе «рабочий». Впрочем, формулу в ячейке D9 можно записать и короче:
«=ЕСЛИ(C9<=5;"рабочий";"выходной")».
А теперь сделаем так, чтобы слово «выходной» выводилось красным цветом (применим условное форматирование):
4 Выделить ячейку D9 Þ команда меню Формат/Условное форматирование Þ в окне Условное форматирование задать условие: значение| равно| выходной Þ кнопка [Формат] Þ в окне Формат ячеек вкладка Шрифт Þ задать цвет шрифта Þ [ОК] Þ [ОК].
Упражнения
11.1. Определить, является ли число в некоторой ячейке положительным или отрицательным. В зависимой ячейке поместить текст «положительное» или «отрицательное».
11.2. Составить формулу для вычисления функции у(х), определенной по следующему правилу:
11.3. Вычислить 
. Если у лежит в заданных пределах [a, b], в зависимой ячейке сформировать соответствующий текст.
11.4. По условиям контракта работнику установлена оплата с коэффициентом 1,25 тарифа за час в рабочий день и коэффициентом 2 за каждый час работы в выходной. Рассчитать дневную оплату при заданных дате, тарифе и количестве отработанных часов.
Работа 12. Адресация ячеек
В зависимости от выполняемых задач в Excel можно использовать либо относительные ссылки, определяющие положение ячейки относительно положения ячейки формулы, либо абсолютные ссылки, которые всегда указывают на конкретные ячейки. Если перед буквой или номером стоит знак доллара, например, $A$1, то ссылка на столбец или строку является абсолютной. Относительные ссылки автоматически корректируются при их копировании, а абсолютные ссылки — нет. Поясним сказанное на примерах.
Задание 12.1. Создать новую книгу с именем «Матрицы».
Пример 12.1. Относительные, абсолютные ссылки.
4 Листу 1 книги «Матрицы» дать имя «Ссылки».
4 В ячейку С3 поместим простенькую формулу, например, «=5*A1».
4 Включим режим отображения формул в ячейках: команда меню Сервис/Зависимости формул/Режим проверки формул.
Для возвращения в обычный режим отображения в ячейках результатов расчетов следует еще раз выполнить эту же команду.
4 Скопируем эту формулу в соседние ячейки по горизонтали: выделить ячейку С3 Þ установить курсор мыши на маркер заполнения Þ произвести копирование.
Видим, что в соседних ячейках появились формулы «=5*B1», «=5*С1» и т. д.
4 Скопируем формулу из ячейки С3 по вертикали и получим последовательность: «=5*A2», «=5*A3»…
Если мы хотим, чтобы при копировании по горизонтали адрес столбца не изменялся, то в формуле ссылку на столбец нужно сделать абсолютной, т.е. формула в ячейке С5 должна быть такой: =5*$A1 (опробовать этот вариант). Знак доллара перед соответствующей координатой означает, что она (координата) при копировании формулы изменяться не будет. Аналогично для того, чтобы при копировании по вертикали адрес строки не изменялся, ссылка на строку должна быть абсолютной: «=5*A$1» (опробовать и этот вариант).
Ну и для того, чтобы при любом копировании ссылка всегда была на одну и ту же ячейку (в нашем случае А1), формула должна быть «=5*$A$1».
Пример 12.2. Имеется таблица стоимости товара в условных единицах. Создать таблицу пересчета стоимости товара в рублях.
Создадим таблицу со следующими столбцами:
| товар | цена 1 шт.; у.е. | количество, шт. | стоимость, у.е. | стоимость, руб |
4 Поместим названия столбцов, начиная с ячейки В10.
4 Ввести данные (5 строк) в столбцы «товар», «цена», «количество».
4В ячейку Е11 ввести формулу расчета стоимости товара «=C11*D11».
4 Скопировать формулу из ячейки Е11 в ячейки Е12:Е15: выделить ячейку с копируемой формулой Е11 Þ установить курсор на маркер заполнения Þ протянуть маркер до ячейки Е15.
4 В ячейку В8 поместим текст: «1 у. е. =», а в ячейку С8 – число, являющееся текущим курсом 1 у. е.
4 В ячейку F11 ввести формулу расчета стоимости товара в рублях: «=E11*C8» Þ скопировать формулу из ячейки F11 в ячейки F12:F15.
Видим, что получилась ерунда (см. далее).
Обратим внимание на ссылки (адреса ячеек) в формулах в ячейках Е12, Е13 и т.д. Видим, что при копировании произошло изменение номеров строк по сравнению с исходной формулой в ячейке Е11 (но именно это нам и надо). Но при расчете стоимости в рублях необходимо, чтобы стоимость в у.е. всегда умножалась на одно и то же число – содержимое ячейки С8. Поэтому:
4 Подкорректируем формулу в ячейке F11: «=E11*$C$8» Þ скопируем формулу из ячейки F11 в ячейки F12:F15.
Теперь второй сомножитель – это всегда ссылка на одну и ту же ячейку: С8.
4 Изменяя содержимое ячейки С8 (курс рубля), сразу получаем пересчет стоимости товара.
Пример 12.3. Имеется прямоугольная матрица А размером 5´3 (5 строк, 3 столбца) и матрица-столбец В (5 строк). Необходимо построить матрицу С размером 5´3, элементы которой есть элементы матрицы А, сложенные с элементами соответствующих строк матрицы В, т.е.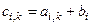 
.
Пусть матрица А расположена в ячейках В23:D27, матрица В – в ячейках F23:F27, а матрица С – в ячейках H23:J27.
4 Заполнить произвольными числами матрицы А (В23:D27) и В (F23:F27) Þ в ячейку Н23 поместить формулу «=B23+F23» Þ скопировать формулу из ячейки Н23 в ячейки Н24:Н27 Þ убедиться, что сложение произошло правильно.
4Скопировать формулу из ячейки Н21 в ячейки I23:J23 Þ убедиться, что сложение произошло НЕПРАВИЛЬНО!
Нам надо, чтобы у второго слагаемого ссылка всегда была на столбец F. Можно, конечно, отдельно построить каждый столбец новой матрицы, но мы поступим более грамотно: ссылку на столбец F надо сделаем абсолютной. Итак:
4 Выделить ячейку Н23 Þ подкорректируем формулу: перед буквой F поставим знак доллара ($), т.е. ссылку на столбец F сделаем абсолютной.
4 Скопировать формулу из ячейки Н23 в ячейки I23:J23.
4 Скопировать строку матрицы H23:J23 в ячейки H24:J27: выделить ячейки H23:J23 Þ произвести копирование вниз (до ячеек H27:J27).
4 Убедиться, что матрица С построена правильно.
Упражнения
12.1. В таблицу примера 12.2 добавить столбец «наценка», который рассчитывается по формуле
наценка = стоимость´(размер наценки).
Размер наценки задается в процентах. Выделить для величины размер наценки отдельную ячейку и произвести расчет наценки.
12.2. В таблицу примера 12.2 добавить столбец «полная стоимость» (стоимость + наценка). Добавить в таблицу столбец «скидка»:
скидка = (полная стоимость) ´ (процент скидки).
Под величину процент скидки отвести отдельную ячейку.
Добавить в таблицу столбец «окончательная стоимость» (стоимость с учетом скидки).
12.3. Выполнить умножение элементов прямоугольной матрицы (размером 3´4) на некоторое число, которое находится в отдельной ячейке.
12.4. Выполнить поэлементное сложение двух матриц одинакового размера 3´4.
12.5. Имеется прямоугольная матрица 3´4. Построить новую матрицу, все элементы которой уменьшены на величину первого элемента исходной матрицы (а1,1).
12.6. Построить таблицу умножения целых чисел от 1 до 10.
Это должна быть таблица, на пересечении строк и столбцов которой находится произведение соответствующих чисел.
Работа 13. Обработка диапазонов
В Excel имеется ряд функций, для которых в качестве аргумента можно задавать диапазон ячеек. Рассмотрим лишь некоторые из них.
Задание 13.1. В книге «Матрицы» листу 2 дать имя «Диапазоны».
Задание 13.2. На листе «Диапазоны» создать массив (матрицу) размером 5´4 в ячейках В3:Е7, заполнив ее произвольными числами. Отформатировать матрицу (рамка, заливка). Эта матрица будет использоваться в последующих примерах.
Пример 13.1. Вычислить сумму элементов каждой строки матрицы В3:Е7.
Суммы разместим в столбце G, в ячейках G3:G7.
4 В ячейку G2 поместить текст «сумма» Þ выделить ячейку G3 Þ Вставка функции Þ Математические Þ выбрать СУММ Þ в окне Аргументы функции в строке Число1 задать диапазон суммирования В3:Е3 (возможно, этот диапазон суммирования уже окажется заданным автоматически, но все-таки удалите его в строке Число1 и вновь задайте методом выделения в исходной матрице) Þ [ОК].
В ячейке G3 должна быть формула «=СУММ(B3:E3)».
4 Скопировать формулу в ячейки G4:G7.
4 Отформатировать столбец с суммами (желательно, чтобы параметры форматирования отличались от тех, которые использовались для форматирования исходной матрицы).
Задание 13.3. По изложенной выше методике вычислить суммы элементов каждого столбца матрицы, разместив их в ячейках В9:Е9. Отформатировать строку с суммами.
Пример 13.2. Вычислить сумму всех элементов матрицы тремя способами: как сумму сумм по строкам, сумму сумм по столбцам, сумму всех элементов матрицы.
4 В ячейки В11:В13 поместим тексты: «сумма по строкам», «сумма по столбцам», «сумма по элементам» Þ в ячейку С11 поместим формулу «=СУММ(B9:E9)» (конечно же, используя механизм вставки функций) Þ в ячейку С12 поместим формулу «=СУММ(G3:G7)» Þ в ячейку С13 поместим формулу «=СУММ(B3:E7)».
Все три суммы должны получиться одинаковыми.
4 Изменяя значения элементов матрицы, наблюдать изменение сумм.
Пример 13.3. Найти наибольшее, наименьшее и среднее значения элементов матрицы.
Воспользуемся функциями: максимальное значение МАКС, минимальное значение МИН, среднее значение СРЗНАЧ из категории Статистические.
4 В ячейки В15:В17 поместим тексты: «наибольшее», «наименьшее», «среднее» Þ в ячейки С15:С17 поместим формулы для вычисления наибольшего «=МАКС(B3:E7)», наименьшего «=МИН(B3:E7)» и среднего «=СРЗНАЧ(B3:E7)» значений.
4 Изменяя значения элементов матрицы, наблюдать за изменением наибольшего, наименьшего и среднего значений.
Пример 13.4. Определить общее количество элементов матрицы и количество отрицательных.
Используем функции СЧЕТ и СЧЕТЕСЛИ из категории Статистические. Функция СЧЕТ подсчитывает общее количество элементов диапазона, функция СЧЕТЕСЛИ лишь количество элементов, удовлетворяющих заданному критерию (наш критерий – отрицательные значения).
4 В ячейки В19:В20 поместим тексты: «всего элементов», «количество отрицательных».
4 В ячейку С19 поместим формулу подсчета общего количества элементов «=СЧЁТ(B3:E7)».
4 В ячейку С20 поместим формулу для подсчета количества отрицательных: вставка функции СЧЕТЕСЛИ Þ в окне Аргументы функции указать диапазон В3:Е7, критерий «<0» (если мы не поставим кавычки, Мастер функций поставит их сам).
4 Изменяя значения элементов матрицы, наблюдать изменение результатов.
Пример 13.5. Вычислить среднее значение элементов матрицы по формуле
.
Мы уже рассчитывали среднее, здесь продемонстрируем другой способ.
4 В ячейку В22 поместим текст «среднее по формуле» Þ в ячейку С22 - формулу «=СУММ(B3:E7)/СЧЁТ(B3:E7)».
4 Сравнить результат с полученным ранее с помощью функции СРЗНАЧ.
Упражнения
Используя созданную матрицу как источник данных, вычислить:
13.1. Сумму элементов первых трех столбцов.
13.2. Сумму элементов 1, 2 и 4-й строк.
13.3. Наибольшее, наименьшее и среднее значения для блока ячеек, состоящего из 3, 4 и 5-й строк.
13.4.Общее количество чисел, превышающих 3.
Работа 14. Матричные вычисления
Существует несколько функций, позволяющих эффективно обрабатывать матрицы, в частности:
- ТРАНСП – транспонирование матрицы;
- МОБР – вычисление обратной матрицы;
- МОПРЕД – вычисление определителя матрицы;
- МУМНОЖ – умножение матриц.
Функция ТРАНСП находится в категории Ссылки и массивы, остальные – в категории Математические.
Формулы, создаваемые с помощью этих функций, используются как формулы массива.
Формула массива позволяет обрабатывать наборы значений. В качестве результата может возвращать как одно значение, так и набор.
Ввод формулы массива заканчивается нажатием комбинации клавиш [Ctrl/Shift+Enter] либо [Ctrl/Shift]+ [ОК] при использовании Мастера функций. При этом формула массива автоматически заключается в фигурные скобки {}.
Задание 14.1. В книге «Матрицы» добавить лист. Дать ему имя «МатрВычисл».
Пример 14.1. В горизонтальном диапазоне ячеек имеется текст. Поменять ориентацию массива с текстом с горизонтальной на вертикальную.
Пример будем выполнять на листе «МатрВычисл».
Пусть, например, в диапазоне В3:Е3 находится массив текстовых значений: «первый», «второй», «третий», «четвертый». Новый массив разместим в ячейках Н3:Н6.
Такая задача может быть решена с помощью функции ТРАНСП, которая возвращает вертикальный диапазон ячеек в виде горизонтального и наоборот. Функция ТРАНСП должна быть введена как формула массива в интервал, который имеет столько же строк и столбцов, сколько столбцов и строк имеет массив-аргумент.
4 В ячейки В3:Е3 поместить: «первый», «второй», «третий», «четвертый» Þ выделить диапазон для вставки Н3:Н6 Þ Вставка функции Þ ТРАНСП (из категории Ссылки и массивы) Þ в окне Аргументы функции Массив: В3:Е3 Þ [Ctrl/Shift+OK] (или [Ctrl/Shift+Enter]).
Пример 14.1а. Другой вариант транспонирования матрицы.
Результат поместим в ячейки К3:К6.
4 Выделить диапазон В3:В6 Þ команда меню Правка/Копировать Þ выделить диапазон для вставки К3:К6 Þ команда меню Правка/Специальная вставка Þ в окне Специальная вставка установить флажок Транспонировать Þ [ОК].
Внешне результат один и тот же, но есть существенная разница. Если мы в исходной матрице изменим какое-нибудь значение (например, «первый» на «десятый»), то при использовании функции ТРАНСП в результирующей матрице также произойдет изменение, а при использовании варианта копирования – нет.
Пример 14.2. Вычислить определитель матрицы.
4 Задать квадратную матрицу размером 2´2 в ячейках В12:С13 Þ выделить ячейку для вставки значения определителя (пусть это будет ячейка Е12) Þ вставить формулу «=МОПРЕД(B12:C13)», используя Мастер функций. Функция МОПРЕД находится в категории Математические. Не забыть закончить ввод формулы нажатием [Ctrl/Shift+OK] или [Ctrl/Shift+Enter].
4Подсчитать вручную определитель матрицы и убедиться в совпадении результатов.
Пример 14.3. Выполнить умножение матрицы размером 3´5 на матрицу размером 5´2.
4 Задать исходные матрицы в ячейках B16:F18 и H16:I20 Þ выделить для размещения результата диапазон K16:L18 размером 3´2 (3 – это количество строк первой матрицы, 2 – количество столбцов второй матрицы) Þ Вставка функции Þ МУМНОЖ (в категории Математические).
4 В окне Аргументы функции в строке Массив1 указать диапазон первой матрицы, в строке Массив2 – диапазон второй матрицы Þ [Ctrl/Shift+OK].
Пример 14.4. Имеется квадратная матрица. Построить обратную матрицу.
Пусть исходная матрица размером 3´3 находится в ячейках С24:Е26. Обратную матрицу поместим в ячейки G24:I26.
4 В ячейки С24:Е26 записать произвольные числа (это исходная матрица).
4 Выделить диапазон G24:I26 для вставки обратной матрицы Þ Вставка функции Þ функция МОБР в категории Математические Þ в окне Аргументы функции в строке Массив указать диапазон исходной матрицы Þ [Ctrl/Shift+OK].
В ячейках G24:I26 должна появиться матрица, обратная исходной.
Если в ячейках результата будет сообщение об ошибке «#ЧИСЛО!», это будет означать, что для исходной матрицы обратная не может быть вычислена. Измените некоторые числа исходной матрицы, и ошибка исчезнет.
4 Для контроля выполнить умножение исходной матрицы на полученную обратную и результат поместить в ячейки К24:М26. Должна получиться единичная матрица.
Внимание!!! Единичная матрица – это квадратная матрица, все элементы главной диагонали которой равны 1, а остальные элементы – 0. В некоторых позициях матрицы вместо нулей могут быть записаны числа порядка 10-15 – 10-18. Это точность, с которой производятся вычисления, так что по сравнению с единицей такие числа можно приближенно считать равными нулю.
Пример 14.5. Решить систему линейных алгебраических уравнений:
В Excel нет функции, позволяющей непосредственно решить систему линейных алгебраических уравнений. Поэтому воспользуемся матричной формой записи уравнения:
A´X=B,
где А – матрица коэффициентов;
Х – матрица-столбец неизвестных;
В – матрица-столбец свободных членов.
Решение можно записать в виде
Х=А-1 ´ В,
где А-1 – матрица, обратная матрице А.
4 В диапазоне В31:С32 разместим матрицу коэффициентов
,
Þ в диапазоне Е31:Е32 – матрицу-столбец свободных членов
.
4 Вычислим и разместим в диапазоне G31:H32 матрицу А-1 (выделим диапазон G31:H32 Þ Вставка функции Þ функция МОБР в категории Математические Þ в окне Аргументы функции в строке Массив указать диапазон исходной матрицы В31:С32 Þ [Ctrl/Shift]+[OK]).
4 Вычислим и разместим в диапазоне J31:J32 произведение А-1 ´ В ( выделим диапазонJ31:J32 Þ Вставка функции Þ функция МУМНОЖ Þ Массив1 G31:H32 Þ Массив2 Е31:Е32 Þ [Ctrl/Shift]+[OK]). Получим матрицу-столбец Х – решение системы уравнений.
4 А теперь для проверки перемножим матрицы А и Х и убедимся, что получилась матрица В.
Пример 14.5а. Решить систему линейных алгебраических уравнений примера 14.5, не создавая на рабочем листе обратную матрицу.
Для решения поставленной задачи в функции МУМНОЖ в качестве первого аргумента используем функцию МОБР:
4 Выделить диапазон М31:М32 для размещения результата Þ Вставка функции Þ функция МУМНОЖ Þ Массив1: МОБР(B31:C32) Þ Массив2: E31:E32 Þ [Ctrl/Shift]+[OK].
4 Сравнить результаты обоих вариантов. Они должны совпадать.
Упражнения
14.1. Создать 2 матрицы: 4´6 и 6´4. Выполнить их умножение.
14.2. Вычислить определитель полученной в упражнении 14.1 матрицы.
14.3. Построить матрицу, обратную полученной в упражнении 14.1. Убедиться, что она действительно обратная.
14.4. Решить систему линейных алгебраических уравнений:
Выполнить проверку полученного решения.
14.5. Выполнить двумя способами транспонирование квадратной матрицы, полученной в упр. 14.1.
Работа 15. Диаграммы
Диаграмма – это общее понятие для группы графических объектов, используемых в Excel для наглядного представления данных.
Задание 15.1. Создать новую книгу с именем «Диаграммы».
Задание 15.2. Листу 1 книги «Диаграммы» дать имя «Продукция». На этом листе построить таблицу, отображающую выпуск сельхозпродукции по месяцам. Таблицу разместить начиная с ячейки В4 (слово «месяц» должно быть в ячейке В5). Отформатировать таблицу. Данные для таблицы приведены ниже.
| Производство животноводческой продукции | ||||
| месяц | молоко, т | мясо, т | шерсть, кг | яйцо, тыс |
| янв | ||||
| фев | ||||
| мар | ||||
| апр | ||||
| май | ||||
| июн | ||||
| июл | ||||
| авг | ||||
| сен | ||||
| окт | ||||
| ноя | ||||
| дек | ||||
| Итоги |
Задание 15.3. Вычислить результаты для строки «Итоги» (произвести суммирование по столбцам).
Пример 15.1. Построить круговую диаграмму, отображающую производство молока с января по май.
4 Инструмент Мастер диаграмм (или команда меню Вставка/Диаграмма…).
4 В окне Мастер диаграмм (шаг 1 из 4) выбрать вкладку Стандартные, тип: Круговая, вид: пусть будет первый вариант Þ [Далее].
4 В окне Мастер диаграмм (шаг 2 из 4) выбрать вкладку Диапазон данных Þ установить курсор мыши в строку Диапазон Þ выделить диапазон С6:С10 Þ установить переключатель Ряды в: в положение в столбцах Þ вкладка Ряд Þ установить курсор мыши в строку Подписи категорий Þ выделить диапазон В6:В10 Þ [Далее].
4 В окне Мастер диаграмм (шаг 3 из 4) вкладка Заголовки Þ Название диаграммы: «Производство молока» Þ [Далее].
4 В окне Мастер диаграмм (шаг 4 из 4) на панели Поместить диаграмму на листе: выбрать имеющемся Þ в списке листов выбрать «Продукция» Þ [Готово].
Диаграмму можно перемещать, изменять ее размеры (используя маркеры).
4 Поэкспериментировать с изменением положения и размеров диаграммы.
4 Увеличить размер диаграммы.
Получившаяся диаграмма не очень информативна. Кроме названия диаграммы практически ничего больше нет. Устраним некоторые упущения, допущенные при работе с Мастером диаграмм.
Пример 15.2. Произвести оформление легенды диаграммы примера 15.1.
Легенда служит для идентификации рядов данных (категорий). Прямоугольник с легендой располагается в области диаграммы, и если навести на него указатель мыши, появится всплывающая подсказка «Легенда».
Оформим внешний вид легенды:
4 Выделить (активизировать) область легенды Þ контекстное меню/Формат легенды Þ в окне Формат легенды, используя вкладки Вид, Шрифт, Размещение, произвести оформление Þ [ОК].
Пример 15.3. Произвести оформление рядов данных диаграммы примера 15.1.
4 Выделить (активизировать) область рядов данных (щелкнуть мышью внутри круга – области рядов данных) Þ контекстное меню/Формат рядов данных Þ в окне Формат ряда данных, используя вкладки Вид, Подписи данных, Параметры, произвести оформление, обратив особое внимание на вкладку Подписи данных Þ [ОК].
Пример 15.4. Изменить оформление одного из секторов диаграммы.
Изменим оформление, например, сектора февраль.
4 Щелкнуть мышью в любом секторе диаграммы (логичнее, конечно, щелкнуть в секторе февраль) Þ еще раз щелкнуть в секторе февраль (чтобы выделить именно этот сектор) Þ контекстное меню/Формат точки данных Þ и далее использовать средства окна Формат элемента данных.
4 Изменить вид и других секторов.
4 Сдвинуть диаграмму, например, вправо, чтобы она не отвлекала нас при выполнении последующих примеров.
Пример 15.5. Построить диаграмму-гистограмму, отображающую производство молока и мяса по месяцам в течение года.
Построим диаграмму в два шага, а потом будем видоизменять ее.
4 Инструмент Мастер диаграмм Þ в окне Мастер диаграмм (шаг 1 из 4) вкладка Стандартные Þ тип: Гистограмма, вид: первый вариант Þ [Далее].
4 В окне Мастер диаграмм (шаг 2 из 4) вкладка Диапазон данных Þ установить курсор мыши в строку Диапазон (очистить, если надо, содержимое строки Диапазон) Þ в таблице с исходными данными выделить диапазон C6:D17 Þ вкладка Ряд Þ на панели Ряд ряду1 дать имя «Молоко», ряду2 – имя «Мясо» Þ установить курсор мыши в строку Подписи по оси Х Þ выделить в таблице диапазон В6:В17 с названиями месяцев Þ [Готово].
4 Добавить на диаграмму ее название: курсор мыши на область диаграммы Þ контекстное меню/Параметры диаграммы Þ вкладка Заголовки Þ Название диаграммы: «Производство молока и мяса» Þ [ОК].
4 Подкорректировать надписи по оси Х: курсор мыши установить на разметку оси Х (появится всплывающая подсказка «Ось категорий») Þ контекстное меню/Формат оси Þ в окне Формат оси поработать с вкладками Шрифт, Выравнивание Þ [ОК].
4 Изменить цвет столбика «Мясо»: установить курсор мыши на любой столбик «Мясо» Þ контекстное меню/Формат рядов данных Þ в окне Формат ряда данных вкладка Вид Þ и т. д.
4 Выполнить цветовое оформление области диаграммы: установить курсор мыши на область диаграммы (всплывающая подсказка Область диаграммы) Þ контекстное меню/Формат области диаграммы Þ в окне Формат области диаграммы вкладка Вид Þ и т. д.
4 Выполнить цветовое оформление области построения диаграммы: установить курсор мыши на область построения диаграммы (всплывающая подсказка Область построения диаграммы) Þ контекстное меню/Формат области построения Þ в окне Формат области построения вкладка Вид Þ и т. д.
Пример 15.6. Построить графики функций sinx и cosx для х от 0 до 360 градусов.
Сначала построим таблицу со значениями функций sinx и cosx, которая будет являться источником данных для построения графиков.
4 В книге «Диаграммы» листу 2 дать имя «Синус».
4 В ячейках В4:Е4 поместим названия столбцов: «х, град», «х, рад», «sinx», «cosx».
4 В столбец «х, град» записать значения х от 0 до 360 (автозаполнение, арифметическая прогрессия, шаг 30).
4 В столбец «х, рад» записать значения х в радианной мере: в ячейку С5 поместить формулу «=РАДИАНЫ(B5)» Þ скопировать эту формулу в ячейки С6:С17.
4 В столбцы «sinx» и «cosx» поместить формулы для расчета этих функций.
А теперь построим графики.
4 Выделить ячейки со значениями функций sinx и cosx (D5:E17) Þ Мастер диаграмм Þ в окне Мастер диаграмм (шаг 1…) вкладка Стандартные Þ тип: график.
4 Просмотреть разные варианты построения графика: выбирать вид графика, нажимать и удерживать кнопку [Просмотр результата].
4 Выберем вариант 4: график с маркерами Þ [Готово].
На рабочем листе должна появиться диаграмма с графиками функций.
Пример 15.7. Изменение внешнего вида графика.
4 Увеличить размеры графика: выделить весь график Þ растянуть область диаграммы путем перемещения маркеров.
4 Изменить цвет фона области построения диаграммы: выделить область построения диаграммы Þ контекстное меню/Формат области построения Þ выбрать вид заливки и рамки области построения диаграммы.
4 Изменить вид области диаграммы: выделить область диаграммы Þ контекстное меню/Формат области диаграммы Þ и т. д.
4 Изменить внешний вид кривой графика: установить курсор мыши в любую точку кривой Þ контекстное меню/Формат рядов данных Þ в окне Формат рядов данных выбрать вкладку Вид Þ поэкспериментировать с внешним видом маркеров и линии графика (попробуйте вариант отсутствия маркера). В ходе эксперимента установите флажок Сглаженная линия и обратите внимание на некоторое изменение внешнего вида кривой графика (она стала более плавной).
Пример 15.8. Изменить внешний вид и обозначение осей графика.
Напомним, что ось Х называется осью категорий, а ось Y – осью значений.
4Поместить курсор мыши на ось Х (должна появиться всплывающая подсказка Ось категорий) Þ контекстное меню/Формат оси.
4 В окне Формат оси выбирая вкладки Вид, Шрифт, Выравнивание, поэкспериментировать с параметрами оси Þ остановиться на наиболее привлекательном варианте.
4 Аналогично установить параметры Вид, Шрифт, Выравнивание для оси Y.
Пример 15.9. Установить разметку шкалы оси Х в соответствии с исходными данными в таблице.
Для разметки оси Х используем данные в ячейках В5:В17.
4 Щелкнуть в области диаграммы Þ контекстное меню/Исходные данные Þ в окне Исходные данные вкладка Ряд Þ щелкнуть в строке ввода Подписи по оси Х Þ задать диапазон В5:В17 значений Х (в исходной таблице выделить столбец со значениями Х (В5:В17) Þ в строке ввода Подписи по оси Х должно появиться выражение «=Синус!$B$5:$B$17» Þ [ОК].
4 Подкорректировать, если надо, внешний вид и обозначение осей графика.
Пример 15.10. Установить пересечение оси Y с осью Х в точке (0,0).
4 Поместить курсор мыши на ось категорий Þ контекстное меню/Формат оси Þ вкладка Шкала Þ сбросить флажок пересечение с осью Y (значений) между категориями Þ [ОК].
Пример 15.11. Добавить на график линии сетки.
4 Установить курсор мыши в любом месте области диаграммы Þ контекстное меню/Параметры диаграммы Þ закладка Линии сетки Þ поэкспериментировать с линиями сетки (устанавливая и сбрасывая флажки Ось Х и Ось У.
4 Поэкспериментировать с внешним видом линий сетки: установить курсор на линию сетки (горизонтальную или вертикальную) Þ контекстное меню/Формат линий сетки Þ вкладка Вид Þ и т.д.
Пример 15.12. Задать границы графика по оси Y.
Предположим, что нам необходимо наблюдать значения кривых по оси Y лишь в определенных пределах, например, от –0,5 до 0,7.
4 Установить курсор на ось Y (появится всплывающая подсказка Ось значений) Þ контекстное меню/Формат оси Þ вкладка Шкала Þ установить минимальное значение (–0,5), максимальное (0,7) Þ сбросить флажки Авто для минимального и максимального значений (если они установлены) Þ [ОК].
4 А теперь установить границы значений по оси Y в пределах от –1 до 1.
Пример 15.13. Дать название диаграмме и осям графика.
4 В области диаграммы контекстное меню/Параметры диаграммы Þ вкладка Заголовки Þ Название диаграммы: «График функции» Þ Ось Х: «градусы» Þ Ось Y: «Синус, косинус» Þ [ОК].
4 Если мало места для размещения названий, можно растянуть всю диаграмму и уменьшить область построения диаграммы (выделить эту область и переместить маркеры).
4 Не нравится шрифт названия диаграммы и названия осей? Установить курсор на нужное название Þ контекстное меню и т.д.
Пример 15.14. Изменить оформление легенды.
4 Область диаграммы Þ контекстное меню/Исходные данные Þ вкладка Ряд Þ на панели Ряд выбрать Ряд1 Þ дать имя «Синус» Þ Выбрать Ряд2 Þ дать имя «Косинус» Þ [ОК].
4 Для изменения вида легенды: курсор мыши на область легенды Þ контекстное меню/Формат легенды и т. д.
Упражнения
15.1. Построить круговую диаграмму,отображающую производство шерсти с июня по декабрь.
15.2. Построить диаграмму-гистограмму, отображающую производство молока, мяса и яиц в течение года.
15.3. Построить график функции 
для х от 0 до 40 с шагом 1.
Выполнить оформление графика.
15.4. Построить график функции 
для х от –6 до 6 с шагом 0,5. Считается, что аргумент х для функции cos задан в радианах.
Выполнить оформление графика.
15.5. Построить график функции 
для х от –7 до 7 с шагом 0,5.
Считается, что аргумент х для функции sin задан в радианах.
Для решения проблемы вычисления функции y при х=0 следует вспомнить первый замечательный предел.
Работа 16. Построение линии тренда
Линия тренда характеризует направление изменения ряда данных. Она используется в задачах прогнозирования, решаемых методами регрессионного анализа.
Задание 16.1. Создать книгу с именем «Задачи». Листу 1 дать имя «Тренд».
Пример 16.1. Имеется ряд из 20 значений (104; 100; 83; 123; 114; 109; 118; 152; 124; 161; 140; 145; 154; 155; 122; 134; 113; 131; 126; 108), характеризующих ежедневное изменение курса доллара к некоторой валюте с названием «денежка». Спрогнозировать поведение денежки по отношению к доллару в ближайшее время.
4В ячейки В3, С3 поместить текст-разметку: «день», «курс, днж» Þ в ячейки В4:В23 внести порядковые номера дней (1..20) Þ в ячейки С4:С23 внести 20 значений курса доллара из предлагаемого ряда.
4Построить график изменения курса доллара: выделить диапазон С4:С23 Þ Мастер диаграмм Þ вкладка Стандартные Þ Тип: График Þ Вид: первый вариант Þ [Готово].
4Задать на графике нужные названия: вобласти диаграммы контекстное меню/Параметры диаграммы Þ в окне Параметры диаграммы вкладка Заголовки Þ Название диаграммы: «Стоимость $1» Þ Ось Х: «дни» Þ Ось Y: «денежки» Þ [ОК].
4Добавить на график линию тренда: установить курсор мыши на линию графика Þ щелкнуть правой кнопкой мыши Þ Добавить линию тренда Þ в окне Линия тренда вкладка Тип Þ вариант Линейная Þ [ОК].
Видим, что линия тренда направлена вверх. Значит ли это, что доллар по отношению к денежке будет все время дорожать? Увы, не все так просто.
Продолжим исследование имеющихся данных.
4Задать параметры линии тренда: установить курсор мыши на линию тренда Þ щелкнуть правой кнопкой мыши Þ Формат линии тренда Þ в окне Формат линии тренда вкладка Параметры Þ установить флажок показывать уравнение на диаграмме Þ [ОК].
На диаграмме появится уравнение линии тренда: y = 1,3203х+111,94. Если уравнение наложилось на график, его можно сместить: выделить (щелкнуть мышью) и переместить рамку. Если нужно, можно растянуть и область диаграммы.
Качество аппроксимации линией тренда фактических данных оценивается величиной R2, значение которой лежит в пределах от 0 до 1. Чем ближе линия тренда к фактическим данным, тем ближе значение R2 к 1.
4Поместить на диаграмму значение R2: установить курсор мыши на линию тренда Þ щелкнуть правой кнопкой мыши Þ Формат линии тренда Þ в окне Формат линии тренда вкладка Параметры Þ установить флажок поместить на диаграмму величину достоверности аппроксимации (R^2) Þ [ОК]. Получим R2 = 0,1414.
4Выполнить аппроксимацию данных полиномом второй степени: установить курсор мыши на линию тренда Þ щелкнуть правой кнопкой мыши Þ Формат линии тренда Þ в окне Формат линии тренда вкладка Тип: Полиномиальная, Степень: 2 Þ вкладка Параметры Þ установит флажки показывать уравнение на диаграмме, поместить на диаграмму величину достоверности аппроксимации (R^2) Þ [ОК]. Получим R2 = 0,5938.
4Поэкспериментировать с разными типами аппроксимации.
Пример 16.2. Попробуем спрогнозировать курс доллара на 5 дней вперед.
4 Активировать диаграмму предыдущего примера Þ установить курсор мыши на линию тренда Þ щелкнуть правой кнопкой мыши Þ Формат линии тренда Þ в окне Формат линии тренда вкладка Параметры Þ на панели Прогноз значение вперед на: задать равным 5 единиц Þ [ОК].
4Поэкспериментировать с разными типами аппроксимации.
Данный пример следует, конечно, рассматривать лишь как демонстрацию некоторого инструмента, а не как рекомендацию произвести расчеты и быстренько бежать в пункт обмена валют.
Упражнения
16.1. Ежегодная популяция зайцев в течение 12 лет в некотором регионе характеризуется рядом значений (2820; 4400; 5390; 5930; 6150; 6440; 6890; 7460; 7490; 7180; 7620; 8010). Подобрать аппроксимацию экспериментальных данных и сделать прогноз на ближайшие 5 лет.
16.2. В некотором не очень чистом месте еженедельный подсчет количества мух дал следующий ряд: 2; 58; 1700; 57000. Определить, через сколько недель количество мух может достичь 1 млрд, если не будет никаких препятствий для их размножения.
Работа 17. Решение уравнений
Для решения оптимизационных задач и уравнений в Excel имеется мощный инструмент – надстройка «Поиск решения». Этот инструмент можно использовать и для численного решения уравнений.
Задание 17.1. Убедиться, что на компьютере установлена надстройка «Поиск решения».
4 Выполнить команду меню Сервис.
Если в раскрывшемся подменю есть команда Поиск решения, значит, надстройка установлена. Если нет, то выполнить установку:
4Команда меню Сервис/Надстройки Þ в окне Надстройки в качестве доступной надстройки установить Поиск решения Þ [ОК].
Задание 17.2. Открыть книгу «Задачи». Листу 2 дать имя «Уравнения».
Пример 17.1. Решить уравнение 
.
Начнем с некоторых уточнений и предварительного анализа задачи.
Прежде всего, следует определить границы переменной х, в пределах которых ведется поиск. Пусть это будет вся числовая ось (-¥; +¥).
Поскольку у нас уравнение третьего порядка, то количество вещественных корней (а эта надстройка позволяет найти только вещественные корни) может достигать 3-х.
Для начала очень полезно (хотя и не обязательно) построить график функции. Выберем для построения графика отрезок [0;3] с шагом 0,2. Если он окажется неудачным, выберем другой. Итак:
4На листе «Уравнения» в ячейки А3:А18 записать значения х от 0 до 3 с шагом 0,2 (арифметическая прогрессия) Þ в ячейку В3 поместить формулу
«=A3^3-4,1*A3^2+4,55*A3-1,375»
Þ скопировать эту формулу в ячейки В4:В18 Þ выделить диапазон В3:В18 Þ Мастер диаграмм Þ вкладка Нестандартные Þ Тип: Гладкие графики Þ [Далее] Þ в окне Мастер диаграмм (шаг 2…) вкладка Ряд Þ Подписи по оси Х: выделить диапазон А3:А18 Þ [Готово].
На графике хорошо видно, что наша кривая трижды пересекает ось Х, следовательно, все 3 корня уравнения вещественные. Можно даже приближено оценить их значения.
Одна попытка применения инструмента «Поиск решения» позволяет найти лишь один корень. Для нахождения трех корней придется сделать, по крайней мере, 3 попытки. При каждой попытке придется задавать некоторое начальное значение х, для выбора которого график функции оказывается очень полезным.
Итак, начинаем.
4В ячейки А21, В21 поместим текст «х», «f(x)» соответственно (это разметка ячеек.
4В ячейку В22 поместим формулу для вычисления функции: «=A22^3-4,1*A22^2+4,55*A22-1,375».
4В ячейку А22 поместим начальное значение х – точку, от которой будет идти поиск корня (пусть это будет 0,2).
4Команда меню Сервис/Поиск решения.
4В окне Поиск решения Установить целевую ячейку: $B$22 (набрать с клавиатуры, а лучше установить курсор мыши в эту строку ввода и щелкнуть мышью в ячейку В22) Þ установить переключатель Равной значению: Þ задать значение 0 Þ Изменяя ячейки: $A$22 Þ [Выполнить].
В окне Результаты поиска решения появится сообщение о том, что решение найдено либо нет.
Если решение найдено, оно находится в ячейке А22. Для наших данных оно найдено и равно 0,5 (сравните со значением на графике).
Обратим внимание на полученное при этом значение функции f(x) – величину порядка 10-7. Теоретически должен получиться 0, но поскольку в надстройке реализован приближенный метод, то все расчеты выполняются с некоторой погрешностью. Впрочем, точностью расчетов можно управлять.
4Аналогичным образом найти оба оставшихся корня, в качестве начального задавая значения х =1 и х =2,2. Должны получиться корни х =1,1 и х =2,5.
Пример 17.2. Найти корни функции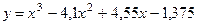 
на отрезке [2;3].
Задача практически та же, что и в предыдущем примере, но здесь есть ограничения на значения переменной х. Эти ограничения нужно указать в окне Поиск решения. Для решения будем использовать ячейки А22, В22 с формулами предыдущего примера.
4В ячейку А22 поместим начальное значение х =1 Þ Сервис/Поиск решения Þ Установить целевую ячейку: $B$22 Þ Равной значению: 0 Þ Изменяя ячейки: $A$22 Þ [Добавить] (нажатие этой кнопки инициирует добавление ограничений) Þ в окне Добавление ограничений Ссылка на ячейку: $A$22 Þ выбрать >= Þ Ограничение: 2 Þ [Добавить] Þ Ссылка на ячейку: $A$22 Þ выбрать <= Þ Ограничение: 3 Þ [ОК] Þ [Выполнить].
Получим х =2,5. Коль скоро мы искали решение на отрезке [2;3], не вполне корректно было задавать начальное значение вне этого отрезка, но решение найти удалось.
Упражнения
17.1. Решить уравнение lnx=1/x. Построить графики функций lnx и 1/х для х от 0,2 до 3 с шагом 0,2. Сравнить результаты графического решения и решения методом подбора параметра.
17.2. Решить уравнение 
.
Указание. Предварительно построить график функции для х от –2 до 2 с шагом 0,2. Из графика определить приближенные значения корней (точки перехода функции через ноль). Их должно быть два. Затем методом подбора параметра уточнить значения корней, задавая в качестве начального значения величины, близкие к найденным из графика.
17.3. Решить уравнение 
.
Величина х задается в радианах. Использовать рекомендации предыдущего упражнения. График функции строить с шагом 0,2.
17.4. Решить уравнение 
.
Работа 18. Решение систем уравнений
Надстройку Поиск решения в ряде случаев можно использовать для решения систем алгебраических уравнений: как линейных, так и нелинейных. Суть подхода к решению задачи: выражение одного из уравнений исходной системы выбирается в качестве целевой функции, остальные уравнения переводятся в разряд ограничений.
Задание 18.1. Открыть книгу «Задачи». Вставить новый лист. Дать ему имя «СистемыУравнений».
Пример 21.1. Решить систему линейных алгебраических уравнений:
Это задача упражнения 14.4.
Переформулируем задачу следующим образом: найти значения переменных (х1, х2, х3, х4), при которых функция
принимает значение, равное 10, при выполнении системы ограничений
4На листе «Системы Уравнений» размечаем ячейки B3:G3: «х1», «х2», «х3», «х4», «правая часть», «вычисл. правая».
4В ячейках В6:Е9 разместим матрицу коэффициентов исходной системы:
.
4В ячейках F6:F9 разместим столбец правых частей системы уравнений: (10, 14, 2, 24).
4Полезно убедится, что определитель системы уравнений не равен нулю, что гарантирует единственность полученного решения. Вычислим определитель, например, в ячейке А3 по формуле «=МОПРЕД(B6:E9)». Для наших данных должно получится -158.
4В ячейку G6 поместим формулу вычисления левой части первого уравнения системы «={СУММ($B$4:$E$4*B6:E6)}», используя методику формулы массива: курсор мыши в ячейку G6 Þ вводим формулу =СУММ($B$4:$E$4*B6:E6) Þ [Ctrl/Shift+Enter].
4Формулу из ячейки G6 копируем в ячейки G7:G9.
4В ячейках В4:Е4 задать произвольные начальные значения переменных, например, все равные 1.
4Команда меню Сервис/Поиск решения Þ Установить целевую ячейку $G$6 Þ Равной: значению 10 Þ Изменяя ячейки: выделить диапазон B4:E4 Þ очистить панель Ограничения (если там были записи) Þ Ограничения: [Добавить] Þ Ссылка на ячейку: выделить диапазон G7:G9 Þ выбрать = (знак равенства) Þ Ограничение: выделить диапазон F7:F9 Þ [ОК] Þ [Выполнить].
В ячейках В4:Е4 должен получиться результат решения системы: (1; 3; 2; 4).
Пример 18.2. Решить систему уравнений с двумя неизвестными
Поступим следующим образом. Первое уравнение (точнее, выражение
зададим в качестве целевой функции, т.е. потребуем, чтобы оно приняло значение, равное нулю, а второе уравнение зададим как ограничение. Итак:
4 В ячейки В14:Е14 поместим обозначения ячеек: «x», «y», «f1», «f2».
4 В ячейку D15 поместим формулу «=B15^2+C15*EXP(B15)-EXP(C15)-1» Þ в ячейку Е15 поместим формулу «=2*B15^3+3*B15*C15-EXP(2*B15)+4».
4В ячейки В15, С15 поместим начальные значения переменных: х =1; у =1.
4Команда меню Сервис/Поиск решения Þ Установить целевую ячейку $D$15 Þ Равной: значению 0 Þ Изменяя ячейки: $B$15:$C$15 Þ очистить панель Ограничения (если там были записи) Þ Ограничения: [Добавить] Þ Ссылка на ячейку: $E$15 Þ выбрать = (знак равенства) Þ Ограничение: 0 Þ [ОК] Þ [Выполнить].
Получаем решение: х @1,052788; у @0,594639.
Попробуем поискать другие решения системы.
4Выполнить поиск для начальных значений х=10; у=0 (решение х @-1,35597; у @-0,2588).
4Выполнить поиск для начальных значений х=20; у=20. После запуска программы на исполнение при этих начальных значениях скорее всего появится окно Текущее состояние поиска решения с сообщением «Достигнуто максимальное число итераций. Продолжить?». Это значит, что предельное количество шагов поиска решения, установленное в программе (по умолчанию это обычно 100), исчерпано. Принимаем решение на продолжение поиска: нажать [Продолжить].
Получаем решение: х @1,634111; у @2,761423.
4Попробуйте поискать решения при других начальных значениях. Вдруг удастся найти еще.
Упражнения
18.1. Решить систему уравнений:
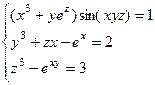
18.2. Решить систему линейных алгебраических уравнений:
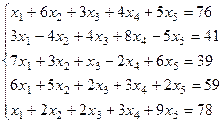
Выполнить проверку полученного решения.
Литература
- Безручко В. Т. Практикум по курсу «Информатика». Работа в Windows, Word, Excel: Учеб. Пособие. М.: Финансы и статистика, 2003.
- Основы информатики: Учеб. Пособие / Ф. Н. Морозевич, Н. Н. Говядинова, В. Г. Левашенко и др.; Под ред. А.Н. Морозевича. Мн.: Новое знание, 2001.
- Символоков Л. В. Решение бизнес-задач в Microsoft Office – М.: Бином, 2001.
