Лекция 8. Свойства оптических резонаторов

Раздел 3. Оптические резонаторы

 

Общие сведения о резонаторах. В самом общем случае резонатором может быть названа всякая колебательная система, в которой возможно накопление энергии колебаний одной или нескольких частот. Такие колебания называются собственными колебаниями резонатора, а их частоты – собственными частотами резонатора.

Если на резонатор действует внешняя периодическая сила, то в нем возбуждаются колебания на частоте этой силы. Такую силу называют вынуждающей, а соответствующие ей колебания и их частоту – вынужденными. Когда частота вынужденных колебаний совпадает с частотой собственных колебаний резонатора, а потери энергии колебаний не превышают определенного уровня, то в системе возникает явление резонанса. Оно состоит в том, что энергия вынуждающей силы переходит в энергию собственных колебаний (мод) резонатора и усиливает их. В этом, собственно, и состоит процесс накопления резонатором колебательной энергии.

Очевидно, что в спектральном отношении процесс накопления является избирательным процессом, поскольку он осуществляется только на частотах собственных колебаний резонатора. Чем меньше этих частот, тем выше избирательные, или, как говорят, резонансные свойства резонатора. Именно наличие высоких резонансных свойств различных резонаторов и обеспечило их широкое практическое применение во многих областях науки и техники.

Существует несколько видов резонаторов, которые отличаются друг от друга видом запасаемой в них энергии. Это механические, акустические и электромагнитные резонаторы. Лазерные резонаторы относятся к последнему виду.

В зависимости от того, в каком диапазоне лежат собственные частоты электромагнитных резонаторов, они могут быть разделены на несколько классов, которые конструктивно очень сильно отличаются друг от друга.

В радиодиапазоне для длинных волн используется простейший резонатор для электромагнитных колебаний – колебательный контур, состоящий из индуктивности L, ёмкости С, сопротивления R; его собственная частота . Размеры таких резонансных контуров много меньше длины волны излучения (). С увеличением частоты размеры контура становятся соизмеримыми с длиной волны, что приводит к резкому возрастанию излучения из контура и он контур теряет свои резонансные свойства. Поэтому в СВЧ-радиодиапазоне при частотах порядка 10⁹…10¹¹ Гц (λ ≈ 0,3…30 см) применяют экранированные резонаторы в виде замкнутых полостей с хорошо проводящими стенками. Это – так называемые объёмные резонаторы. Линейные размеры этих резонаторов сравнимы с длиной волны. Поэтому спектр собственных колебаний этих резонаторов сильно разрежен. Как правило, в диапазоне СВЧ сравнительно просто реализуются такие конфигурации объемных резонаторов, при которых в широком диапазоне частот резонатор обладает одним собственным колебанием. Резонаторные системы СВЧ определяют частоту генерации автоколебательных систем СВЧ.

При дальнейшем увеличении частоты и переходе в субмиллиметровый или ИК диапазон изготовление объемных резонаторов с размерами порядка длины волны становится технологически невозможным. Поэтому необходим переход к резонаторам с размерами, много большими длины волны. Здесь, однако, следует принимать во внимание еще одно обстоятельство. В большом по сравнению с длиной волны замкнутом объеме число осцилляторов поля в единичном объеме и единичном спектральном интервале совпадает с таковым для свободного пространства. Это число, равное

(6.1)

 

было введено при обсуждении вопроса о вероятностях спонтанного и индуцированного излучений (см., например, (2.13)). В объеме V и в частотном интервале Δ ν общее число осцилляторов поля составляет

 

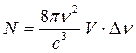(6.2)

 

Очевидно, что увеличение частоты приведет к резкому увеличению числа одновременно возбуждаемых мод. Одновременно с этим наблюдается расширение спектральной линии каждой моды. В результате резонансные линии перекрываются, образуя непрерывный спектр, и резонатор теряет свои резонансные свойства. Итак, в оптическом диапазоне резонатор типа замкнутой металлической полости больших по сравнению с длиной волны размеров не может быть применен в силу высокой плотности его собственных колебаний, приводящей к потере резонансных свойств. Необходимы большие резонаторы с разреженным спектром собственных колебаний.

Выход был найден в том, что вместо закрытых резонаторов здесь стали применять так называемые открытые резонаторы. Эти резонаторы отличаются от полых металлических тем, что у них отсутствует боковая поверхность и они представляют собой всего две отражающие пластины, расположенные на некотором расстоянии друг от друга. Очевидно, что устранение боковых граней резко снижает число мод резонатора, так как стоячие волны в направлениях под большими углами к его оси в этом случае не могут возбуждаться. В результате частотный спектр мод из сплошного превращается в разреженный и резонатор вновь обретает свои резонансные свойства. Более того, в открытых резонаторах, так же как и в объемных, сравнительно просто реализовать такие конфигурации, при которых в широкой области оптических частот они будут обладать всего одной модой.

Именно открытые резонаторы и применяются в качестве лазерных резонаторов, являясь их важнейшим элементом и существенным образом влияя на характеристики генерируемого ими излучения.

Любой резонатор принято называть пассивным, если энергия подводится к нему извне; если эта энергия образуется внутри резонатора, то его принято называть активным.

Применительно к лазерным резонаторам это правило должно пониматься следующим образом: если внутри резонатора активная среда отсутствует, то его следует считать пассивным, если же она присутствует, то его следует считать активным. Отсюда следует, что, вообще говоря, лазерный резонатор – это всегда активный резонатор.

Тем не менее, в лазерной физике принято при изучении процесса формирования поля излучения в резонаторах сначала рассматривать пассивные резонаторы, зачастую даже и ограничиваясь только этим рассмотрением. Исторически сложилось так, что большинство расчетных работ, опубликованных в научной печати, посвящено именно пассивным резонаторам.

Это объясняется не только серьезными трудностями, возникающими при исследовании активных резонаторов. Дело в том, что пассивный резонатор позволяет получить в первом приближении вполне реалистическую картину процессов формирования светового поля в лазерном резонаторе.

Потери энергии в резонаторе. Таким образом, открытые резонаторы являются удобными резонансными системами для квантовой электроники оптического диапазона. Собственные колебания (типы колебаний) резонатора принято называть его модами. По более точному определению мода резонатора – это распределение поля в резонаторе, воспроизводящееся при многократном распространении волны между зеркалами резонатора. Наличие реальных потерь энергии приводит к затуханию колебаний, соответствующих той или иной моде, если только развитие моды не поддерживается излучением активной среды. Рассмотрим лазерный резонатор, который образован двумя плоскими и параллельными друг другу зеркалами, расположенными на расстоянии 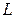одно от другого.

Пусть потери энергии излучения, распространяющегося в виде той или иной колебательной моды резонатора между его зеркалами, описываются некоторым эквивалентным коэффициентом поглощения α, учитывающем потери связанные с поглощением, рассеянием, пропусканием зеркал, дифракцией, неточностью юстировки и пр. Математически влияние этих потерь на величину энергии можно учесть в уравнении, которое называется уравнением баланса и записывается в виде

 

, где . (6.3)

 

Иногда уравнение баланса удобнее записать не для энергии, а для интенсивности излучения. В этом случае уравнение баланса имеет вид

 

. (6.4)

 

Здесь введены следующие обозначения:

- показатель потерь, обусловленный поглощением излучения внутрирезонаторной средой и поверхностью зеркал;

- показатель потерь, обусловленный процессом рассеяния излучения на неоднородностях внутрирезонаторной среды и поверхностей зеркал;

- показатель потерь, обусловленный пропусканием зеркал, благодаря чему генерируемое лазером излучение выводится из резонатора и может быть использовано по назначению;

- показатель потерь, обусловленный дифракцией излучения на различных внутрирезонаторных элементах и зеркалах;

- показатель потерь, обусловленный неточностью юстировки зеркал, т.е. их нестрогой параллельностью;

- показатель других видов потерь, из которых можно назвать, например, потери, обусловленные различными нелинейными процессами внутри резонатора.

Особо следует подчеркнуть то обстоятельство, что в лазерной физике различные виды потерь имеют неодинаковый характер. Например, процессы поглощения и рассеяния, а также неточность юстировки резонатора всегда являются вредными, или, как говорят, “паразитными” потерями. С другой стороны, потери, обусловленные пропусканием зеркал, всегда следует считать полезными.

Особое значение в открытых резонаторах имеет вопрос о дифракционных потерях. Прежде всего следует отметить, что именно дифракционные потери осуществляют прореживание спектра собственных колебаний при переходе от замкнутой полости к открытому резонатору, исключая в процессе установления резонансной моды колебания, распространяющиеся под сколько-нибудь заметными углами к оси резонатора. Наличием дифракционных потерь открытые оптические резонаторы отличаются от замкнутых объемных резонаторов СВЧ. Конечно, как отмечено выше, это не единственный источник потерь, а во многих случаях даже не главный. Но в случае идеальных зеркал и идеальной межзеркальной среды потери энергии, обусловленные дифракцией на краях зеркал с конечной апертурой, остаются принципиально неустранимым, а потому принципиально важным источником потерь.

Иногда в литературе наряду с показателем потерь, который, как нетрудно видеть, имеет размерность см^-1, вводится безразмерный коэффициент поглощения энергии излучения за один проход резонатора длины L. Его определяют как .

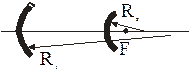
Число Френеля. Пусть в плоскопараллельном резонаторе, образованном двумя круглыми зеркалами с радиусом а, световая волна, отраженная от первого зеркала, дифрагирует в угол, который называется дифракционным и имеет величину

(6.5)

 

Чем меньше этот угол по сравнению с углом поля зрения , т.е. углом, под которым второе зеркало видно из центра первого зеркала, тем эффективнее “перехватывает” второе зеркало излучение, распространяющееся от первого зеркала. Следовательно, тем меньше будут потери излучения за счет дифракции (рис. 6.1).

Угол поля зрения можно выразить как

 

, если . (6.6)

 

Тогда для уменьшения дифракционных потерь следует потребовать выполнения условия

или . (6.7)

 

Запишем это условие в несколько ином виде:

. (6.8)

Величина является безразмерной и называется числом Френеля. Это число является важным физическим параметром резонатора и определяет многие его свойства.

Чтобы выяснить физический смысл этого параметра, обычно производят разбиение отражающей поверхности второго зеркала на зоны Френеля, которые наблюдаются из центра первого зеркала. Затем путем несложных вычислений показывают, что число Френеля равно числу этих зон.

Хотя данная физическая трактовка числа Френеля имеет фундаментальное значение, она мало что дает в понимании его “лазерного” смысла. Поэтому применительно к лазерной физике имеет смысл трактовать его по-другому. Естественно ожидать, что этот параметр определяет величину потерь. Грубую оценку можно сделать в предположении плоских волн. Нетрудно увидеть, что пучок света, содержащий почти плоскую волну, отраженную, скажем, от левого зеркала радиуса а и достигшую после прохождения пути L правого зеркала того же радиуса а, уширяется по радиусу на . Излучение, попадающее в кольцо площадью , выходит из резонатора. Его относительная доля, в предположении однородности распределения амплитуды светового поля по сечению пучка, дает оценку дифракционных потерь энергии за один проход

(6.9)

 

Чем больше число Френеля, тем меньше дифракционные потери. Приведенная оценка, сколько-нибудь разумная только при больших , правильно оценивает только тенденцию зависимости дифракционных потерь от . В реальности в модах резонатора распределение поля по поперечному сечению сильно отличается от однородного, заметно спадая к краям. Поэтому дифракционные потери оказываются существенно меньше предсказываемых формулой (6.9).

В дополнение к сказанному заметим, что фактически число Френеля было нами определено как отношение угла поля зрения x к углу дифракции 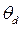(см. (6.7)). Смысл этого отношения состоит в том, что оно определяет наибольшее число проходов излучения в резонаторе, которое оно может совершить при заданном уровне дифракционных потерь до того момента, как покинет резонатор через его открытую боковую поверхность. Значит, оно определяет число проходов излучения через активную среду лазера, т.е. число актов усиления. Для типичных твердотельных лазеров N _F равно сотням, а для газовых – десяткам единиц.

Добротность резонатора. Оптические резонаторы, так же как и их низкочастотные радиочастотные и микроволновые аналоги, используются в первую очередь для получения высоких интенсивностей поля при небольшой входной мощности. Это возможно только в том случае, если резонатор способен эффективно накапливать энергию собственных колебаний.

Однако резонатор не может сохранять накопленную энергию неопределенно долго, так как при отражении электромагнитной волны от зеркал ее энергия теряется вследствие поглощения отражающими покрытиями и пропускания ими света, необходимого для вывода излучения. Кроме того, часть ее энергии теряется из-за дифракции.

Универсальным параметром, характеризующим накопительное свойство резонаторов, является их добротность. Она определяется как величина, обратно пропорциональная скорости уменьшения энергии поля в резонаторе. Аналитически ее выражают в виде отношения запасенной в резонаторе энергии к энергии, теряемой им за один период колебаний .

. (6.10)

Иногда коэффициент в формуле (6.10) не учитывают.

Воспользуемся выражением (6.10) и получим конкретные формулы для добротности резонатора лазера.

1. Пусть в резонаторе объемом 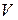имеет место собственное колебание (мода) на частоте . Пусть в начальный момент времени в этой моде запасена энергия поля 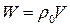, где – начальная объемная плотность этой энергии. При распространении от зеркала к зеркалу вдоль оси резонатора данная мода испытывает потери своей энергии, определяемые выражениями (6.3) или (6.4). Обозначим эти потери через суммарный (эквивалентный) показатель потерь и, используя известную формулу , где – скорость света, перепишем уравнение баланса энергии в виде 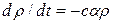. Интегрированием этого уравнения нетрудно получить его решение в виде

. (6.11)

где .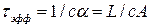

Это решение свидетельствует об экспоненциальном характере затухания моды резонатора с характерным временем 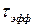, которая называется временем жизни фотона в моде.

2. С помощью (6.11) можно легко получить выражение для добротности рассматриваемого резонатора на частоте его моды . Действительно, запасенная в начальный момент энергия этой моды равна , а ее убыль за один период колебаний можно записать в виде

 

. (6.12)

и, согласно (6.10), получаем

 

. (6.13)

 

При выводе (6.13) полагалось , что практически всегда имеет место. С учетом (6.11), формула (6.13) принимает простой вид

 

. (6.14)

 

Отсюда следует, что чем больше потери резонатора, тем меньше его добротность. Таким образом, с помощью понятия добротности можно характеризовать диссипативные свойства резонатора на его собственных частотах. Покажем это на следующем примере.

3. Перепишем уравнение баланса энергии резонатора так, чтобы в нем в явном виде содержалась добротность (6.14):

 

. (6.15)

 

Легко видеть, что решение этого уравнения имеет вид

 

или . (6.16)

Отсюда следует, что соответствующие коэффициенты затухания энергии и интенсивности обратно пропорциональны величине добротности.

4. Перейдем теперь к рассмотрению резонансных свойств резонатора. Так как изменение его энергии во времени известно, то из (6.16) можно получить и выражение для изменения во времени напряженности поля:

. (6.17)

 

Используя преобразование Фурье, можно записать

 

, где . (6.18)

 

Нижний предел интегрирования в взят нулевым, так как функция существует только в области . Функция имеет смысл спектральной плотности поля, что очевидно следует из ее размерности. Она представляет собой спектральное разложение внутрирезонаторного поля, т.е. определяет амплитуды его различных частотных компонент.

Чтобы вычислить эту функцию, подставим (6.17) в и возьмем интеграл. Тогда

(6.19)

 

где 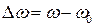– отстройка частоты спектральной компоненты от центральной частоты моды. Действительная часть выражения (6.19) равна

 

, (6.20)

 

и определяет амплитуду этой компоненты, а функция

 

, (6.21)

 

определяет закон, по которому изменяется амплитуда при изменении ее частоты. График функции (6.21) имеет вид нормированной кривой (рис. 6.2), которая называется резонансной кривой резонатора или его спектральной линией и имеет лоренцеву форму. Ширина этой линии, определенная на ее полувысоте, т.е. когда , равна

. (6.22)

и часто называется полосой пропускания резонатора. Иногда пользуются понятием полуширины этой линии .

С учетом (6.22), выражения (6.20) и (6.21) принимают вид:

 

, . (6.23)

 

Проанализируем полученные результаты. Из формул (6.22) и (6.23) следует, что чем выше добротность резонатора, т.е. чем ниже его потери, тем меньше ширина соответствующей резонансной кривой и тем больше амплитуда поля соответствующей моды. В этом случае принято считать, что резонансные свойства у такого резонатора более выражены. И наоборот, модам с меньшей добротностью соответствуют более высокие потери, более широкая резонансная кривая и меньшая величина амплитуды. Высокодобротные моды обычно распространяются вблизи оси пассивного резонатора, поскольку для них дифракционные потери меньше.

Заметим, что формула (6.22) позволяет по-новому определить добротность резонатора

. (6.24)

Сравнивая (6.24) с (6.13), получаем, что

 

, (6.25)

 

т.е. время жизни фотона в моде обратно пропорционально ширине спектральной линии этой моды.

Типы лазерных резонаторов. Как отмечалось выше, спектрально-пространственные характеристики и параметры лазерных пучков почти полностью определяются геометрией резонаторов. Поэтому конфигурация резонаторов может быть положена в основу классификации лазерных пучков по типам. В технике резонаторов принято считать, что каждой конфигурации соответствует свой, вполне определенный, тип резонатора. 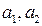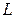В случае круглых зеркал любую конфигурацию можно полностью задать пятью геометрическими размерами: – радиусы зеркал; – радиусы их кривизны; – расстояние между зеркалами, т.е. длина резонатора. В случае прямоугольных зеркал число независимых размеров возрастает до семи, так как вместо радиусов зеркал необходимо использовать размеры их сторон. На практике при определении типа резонатора его геометрические размеры задаются не в явном виде, а в виде некоторых комбинаций, имеющих определенный физический смысл. Наиболее часто используют обобщенные параметры резонатора

 

, , (6.26)

 

которые, как будет показано ниже, определяют модовый состав излучения. При расчете следует правильно учитывать знак радиусов кривизны зеркал: если зеркало своей вогнутой поверхностью обращено внутрь резонатора, то радиус его кривизны имеет положительное значение, а если во вне – отрицательное. Другой комбинацией геометрических размеров являются числа Френеля

, , (6.27)

 

или же циклические аналоги

 

, , (6.28)

 

которые называются циклическими числами Френеля и также определяют дифракционные потери излучения в резонаторе.

В таблице 1 приведены конфигурации наиболее известных типов резонаторов и даны их общепринятые названия.

Наиболее распространенными являются три конфигурации – плоскопараллельная, конфокальная и концентрическая. Для плоскопараллельной конфигурации и она является всегда симметричной. Для конфокальной конфигурации 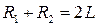и она образует совмещение фокусов зеркал 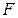. Если одно из зеркал, например второе, является выпуклым, то условие конфокальности принимает вид 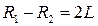, и общий фокус зеркал выносится за резонатор (телескопический конфокальный резонатор). При конфокальный резонатор становиться симметричным. Если одно из зеркал заменить на плоское и поместить его в фокусе другого зеркала, то такой резонатор будет называться полуконфокальным (). Для концентрической конфигурации выполняется равенство , и она получается совмещением центров сфер поверхностей зеркал. При , концентрический резонатор превращается в симметричный и называется сферическим, так как этом случае поверхности его зеркал лежат на одной и той же сфере радиуса . Все другие конфигурации резонаторов следует считать произвольными.

 

Таблица 1

№	Конфигурация	g1	g2	Наименование
				Плоскопараллельный резонатор
				Конфокальный резонатор
				Конфокальный симметричный резонатор
			0.5	Полуконфокальный резонатор
				Телескопический конфокальный резонатор
				Концентрический резонатор
		-1	-1	Концентрический симметричный (сферический) резонатор
				Полуконцентрический (полусферический) резонатор

 

В технике резонаторов их работу принято рассматривать с точки зрения устойчивости (стабильности), в связи с чем кроме классификации резонаторов по геометрическим размерам их можно условно подразделить на два класса – класс устойчивых и неустойчивых резонаторов.

Устойчивость работы резонаторов. Свойства резонаторов и характеристики создаваемых ими пучков можно описывать и в волновом, и в геометрической приближении. В качестве критерия применимости этих приближений удобно использовать число Френеля. При этом для применимости геометрического приближения необходимо выполнение условия

, (6.29)

 

а для применимости волнового – условия

 

. (6.30)

Резонатор называется устойчивым, если при многократных проходах излучения между зеркалами электромагнитное поле имеет стационарный характер, а его распределение воспроизводится идентично. В приближении геометрической оптики (6.29) это означает, что излучение не выходит за пределы зеркал в поперечном направлении и выводится только благодаря частичному пропусканию зеркал. Поэтому в устойчивом резонаторе, в случае отсутствия потерь, излучение могло бы существовать бесконечно долго.

В неустойчивом резонаторе световые пучки (или описывающие их электромагнитные волны) в результате последовательных отражений от зеркал перемещаются в поперечном направлении от оси резонатора к его периферии и покидают его.

В геометрическом приближении условие устойчивости работы резонатора может быть записано в виде

 

. (6.31)

 

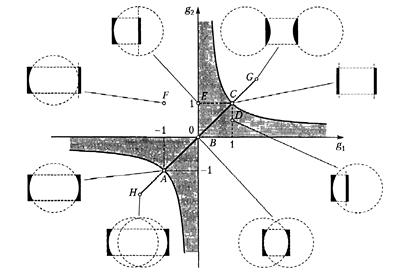
На рис. 6.3 это условие представлено в графическом виде в – координатах, что позволило наглядно представить область устойчивости (штрихованная область) и область неустойчивой (нештрихованная область) работы резонатора.

График рис. 6.3 позволяет дать обобщенный анализ устойчивости работы резонаторов всех типов. Для этого проведем биссектрису углов 1-й и 3-й четвертей координатной плоскости и рассмотрим сначала те типы резонаторов, параметры которых соответствуют точкам, лежащим на этой биссектрисе. Так как для точек биссектрисы справедливо выполнение равенства , из которого следует равенство , то соответствующие резонаторы называется симметричными.

Анализируя устойчивость работы симметричных резонаторов, будем последовательно перемещаться вдоль биссектрисы от точки к точке . При этом наблюдается следующая закономерность:

В области отрезка диаметр кривизны зеркал резонатора всегда меньше его длины , поэтому такой тип резонатора всегда будет неустойчивым, так как излучение довольно быстро покидает внутрирезонаторную область через открытую боковую поверхность.

Будем мысленно увеличивать радиусы зеркал до тех пор, века в точке B диаметр кривизны их поверхности не сравняется с длиной резонатора . В этом случае резонатор становится устойчивым концентрическим резонатором.

При дальнейшем увеличении радиусов зеркал режим работы резонатора будет устойчивым вплоть до того момента, когда они становятся плоскими в точке , которой соответствует плоскопараллельный резонатор, являющийся устойчивым типом. При этом промежуточной точке , в которой , соответствует симметричный конфокальный резонатор.

Точки, лежащие на отрезке , соответствуют симметричным резонаторам с выпуклыми зеркалами, так как в этой области , что соответствует условию . Это область неустойчивой работы резонаторов, так как в этом случае излучение быстро покидает резонатор через его боковую поверхность.

Для несимметричных резонаторов и соответствующие им точки лежат вне биссектрисы. При этом каждому несимметричному резонатору соответствуют две точки, которые расположены симметрично относительно биссектрисы. Эти точки переходят друг в друга при перестановке зеркал резонатора . Например, точки соответствуют полуконфокальному, а точки Е – полуконцентрическому резонатору.

Устойчивые резонаторы сравнительно просты в эксплуатации, легко юстируются и достаточно устойчивы к разъюстировке. Высокое оптическое качество их зеркал сравнительно легко достигается при изготовлении. Все это обеспечило им широкое распространение в лазерной технике, особенно в технике маломощных (£ 1кВт) лазеров. К числу их недостатков относится то, что активная среда при использовании устойчивых резонаторов заполняется излучением неравномерно, вследствие чего их КПД снижается и для повышения мощности приходится увеличивать размеры лазера. Кроме того, при малых размерах перетяжки пучка может происходить оптический пробой, который приводит к выходу из строя различных оптических элементов резонатора. Однако самым серьезным недостатком является то, что зеркала устойчивых резонаторов обладают невысокой лучевой стойкостью из-за выгорания их диэлектрических покрытий. Именно это обстоятельство ограничивает их применение в конструкциях лазеров большой мощности.

Наибольшее распространение среди устойчивых резонаторов получил полуконфокальный резонатор, что объясняется, в основном, параллельностью его выходного пучка и возможностью использования для вывода излучения плоских окон из частично прозрачных материалов. В них возможно применение и металлических зеркал с отверстием в одном из них для вывода излучения, что, однако, не всегда является удобным.

Указанные недостатки устойчивых резонаторов привели к тому, что при создании высокомощных технологических лазеров стали использовать неустойчивые резонаторы со сферическими металлическими зеркалами. Наиболее часто в таких лазерах используют телескопический конфокальный резонатор, который подробнее будет рассмотрен нами ниже.

И, наконец, следует отметить, что четкая граница по потерям между устойчивыми и неустойчивыми резонаторами существует только в рамках геометрического приближения, когда соответствующие числа Френеля достаточно велики. В реальных случаях переход в неустойчивую область всегда сопровождается более или менее крутым нарастанием потерь, причем крутизна нарастания определяется числом Френеля – чем больше это число, тем больше крутизна нарастания и соответственно тем резче график рис. 6.3. В общем случае кривые этого графика будут как бы «размыты» в некоторую полосу, ширину которой можно трактовать как ширину переходной области от устойчивого к неустойчивому режиму работы резонатора.